알고리즘
- 다이나믹 프로그래밍
tip
다이나믹 프로그래밍 문제 해결하는 방법
- 큰 문제를 보다 작은 문제들의 합으로 재귀적으로 푸는 방법을 찾는다.
- 이전의 값을 저장해서 반복적인 계산을 최소화한다.
풀이
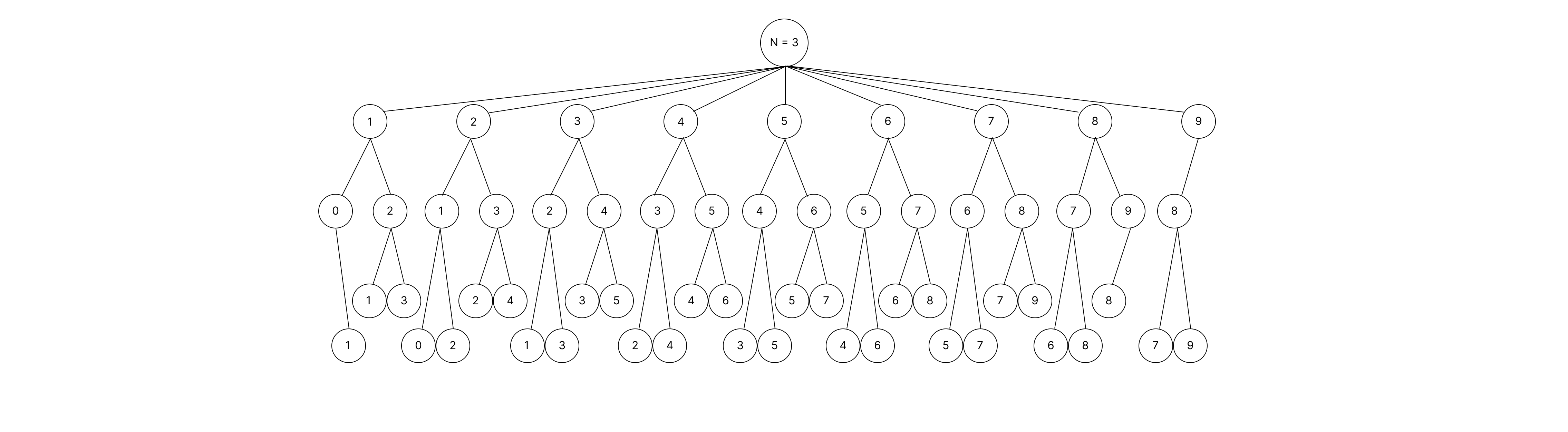
N=3 일 때, 모든 경우의 수를 나타내면 다음과 같다.
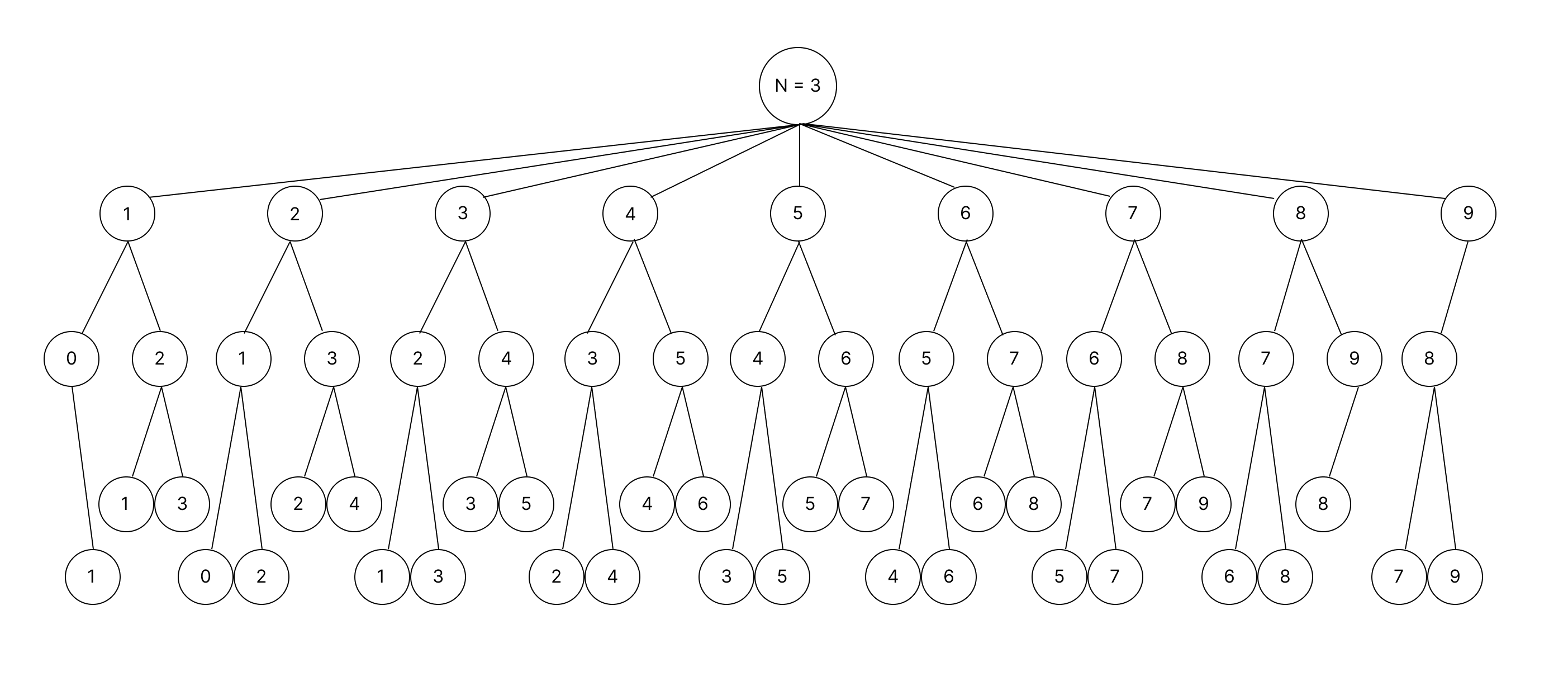
N=3에서 총 경우의 수는 32 (밑의 가지들을 모두 더해서 구한다)
그렇다면 반복적인 계산은 어떤게 있을까?
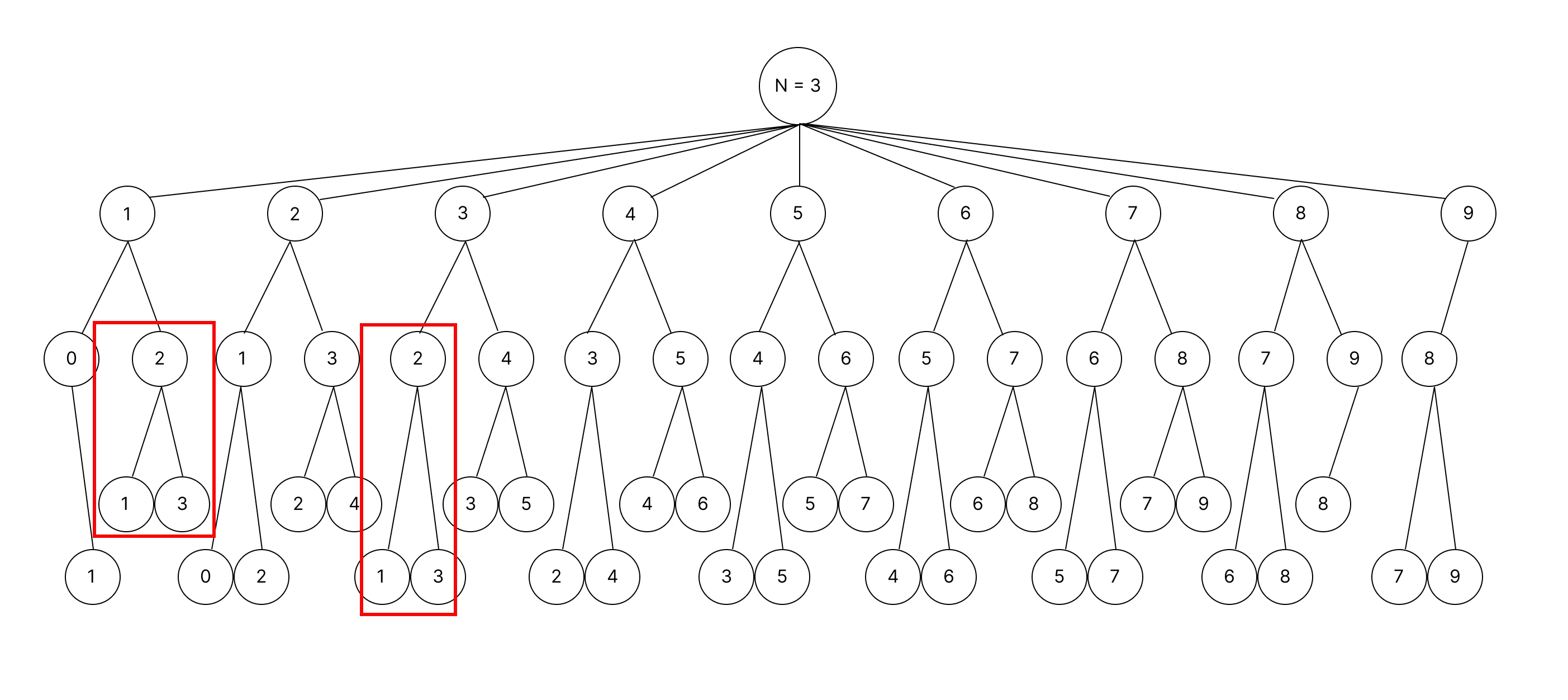
그림과 같이 같은 라인의 숫자 2 이후부터 경우의 수가 1과 3으로 같다.
마찬가지로 같은 라인의 3,4,5,6,7,8 의 숫자들이 두번씩 반복된다.
반복되는 계산을 모두 제외하면 아래와 같다.

포인트
같은 라인(자릿수) 에서 같은 숫자가 나오면 값을 저장해 놓는다.
변수가 두 개 - 같은 자릿수 & 같은 숫자 이므로 이차원 리스트를 활용한다.
코드
n 자리에서의 경우의 수 =
n-1 자리에서의 경우의 수 + n+1 자리에서의 경우의 수
메모이제이션 적용 전 코드
import sys
# 재귀 호출 제한 해제
sys.setrecursionlimit(100000000)
n = int(input())
res = 0
# s -> "0" ~ "9"
def dfs(s):
# 목표 자릿수에 도달하면
if len(s) == n:
return 1
# 9 -> 8
if s[-1] == "9":
return dfs(s + "8")
# 0 -> 1
if s[-1] == "0":
return dfs(s + "1")
else:
return dfs(f"{s}{int(s[-1])+1}") + dfs(f"{s}{int(s[-1])-1}")
# 1부터 9까지의 경우의 수를 각각 구해서 합치기
for i in range(1, 10):
res += dfs(str(i))
print(res % 1000000000)입력으로 3을 넣으면 32가 알맞게 출력된다. 하지만 100을 넣으면 엄청 오래 걸린다.
메모이제이션 적용한 코드(정답 코드)
import sys
# 재귀 호출 제한 해제
sys.setrecursionlimit(100000000)
n = int(input())
# 메모이제이션
# 행 -> 자릿수
# 열 -> 숫자
memo = [[0 for _ in range(10)] for _ in range(n + 1)]
res = 0
# s -> "0" ~ "9"
def dfs(s, i):
# 이전에 구했던 자릿수 & 숫자와 일치하면 결과 재사용
if memo[i][int(s[-1])]:
return memo[i][int(s[-1])]
# 목표 자릿수에 도달하면
if len(s) == n:
# print(s)
return 1
# 9 -> 8
if s[-1] == "9":
cnt = dfs(s + "8", i + 1)
memo[i][int(s[-1])] = cnt
return cnt
# 0 -> 1
if s[-1] == "0":
cnt = dfs(s + "1", i + 1)
memo[i][int(s[-1])] = cnt
return cnt
else:
cnt = dfs(f"{s}{int(s[-1])+1}", i + 1) + dfs(f"{s}{int(s[-1])-1}", i + 1)
memo[i][int(s[-1])] = cnt
return cnt
# 1부터 9까지의 경우의 수를 각각 구해서 합치기
for i in range(1, 10):
res += dfs(str(i), 1)
print(res % 1000000000)
최적화한 코드다.
함수 마지막 return 부분에 print 함수로 출력해보면
입력으로 100을 넣었을 때 최적화 없이 마지막까지 구한 경우가 18번 밖에 되지 않는다.
