1. Support vector machine(SVM)
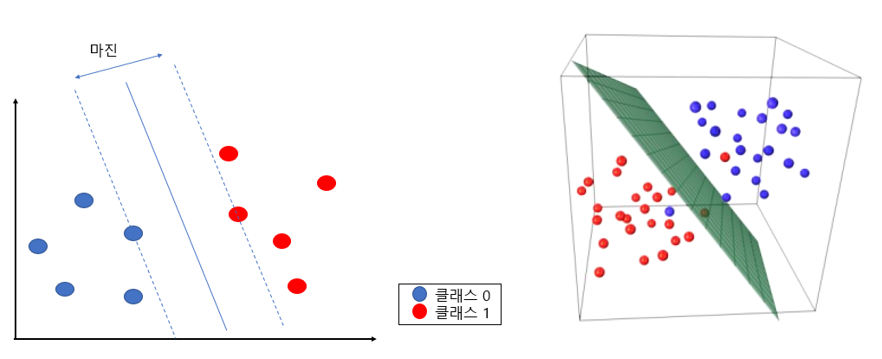
최대 마진(Maximum Margin)을 가지는 결정 경계를 이용하는 분류, 회귀 기법.
이진 분류 모델에서는 class0과 1을 구분하기 위한 최적의 경계를 탐색
SVM는 데이터를 분류할 때, 마진(magin)을 최대화하는 방식으로 경계를 추론함
이때, support vector(서포트 벡터)란 마진에서 가장 가까이 위치한 각 class의 data (class의 support vector(서포트 벡터)의 위치에 따라, 경계(초평면)의 위치가 달라짐)
즉, SVM은 데이터를 분리하는 최적의 초평면, 즉 최대 마진이 되도록 클래스를 분류하는 기법
- 결정 경계(Decision Boundary) : 서포트 벡터들을 기준으로 생성된 경계로, 이를 기준으로 데이터 포인트의 클래스가 결정된다.
1-0. SVM 의 종류
A. 선형 SVM
:데이터가 선형적으로 분리 가능할 때 사용. 결정 경계는 선형(직선 또는 평면)
선형 SVM은 선형으로 데이터의 클래스를 나눌 수 있는 경우 사용되며 크게 하드마진과 소프트마진 방식으로 나눠진다.
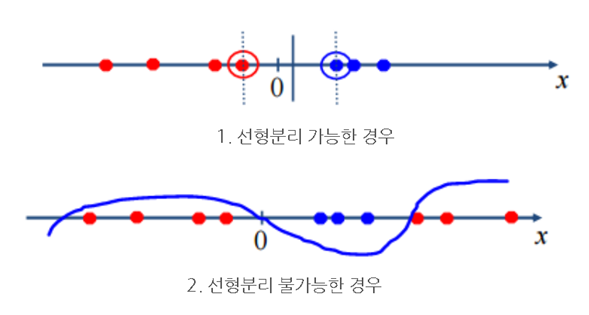
B. 비선형 SVM
: 선형적으로 분리 불가능한 데이터에 커널 트릭을 사용하여 고차원으로 매핑한 후, 선형 SVM을 적용. 가장 일반적인 커널에는 다항식 커널, 라디알 기저 함수(Radial Basis Function, RBF 또는 가우시안 커널), 시그모이드 커널 등이 있다.
1-1. 초평면(Hyperplane)
최대 마진 분류기가 선형 경계로 사용하는 선을 초평면(Hyperplane)이라고 하는데, 데이터가 n차원이라면 초평면은 n-1차원을 가진다. 초평면은 n차원 공간을 두개의 부분으로 이등분한다.
1-2. 분리 초평면(Separating Hyperplane)
훈련 관측치들을 클래스 라벨에 따라 완벽하게 분리하는 초평면(Hyperplane)는 여러 개가 존재할 수 있다.
관측치들을 클래스 라벨에 따라 완벽하게 분리하는 초평면들을 분리 초평면(Separating Hyperplane) 들 중 > 최적의 분리 초평면을 선택해야 함.
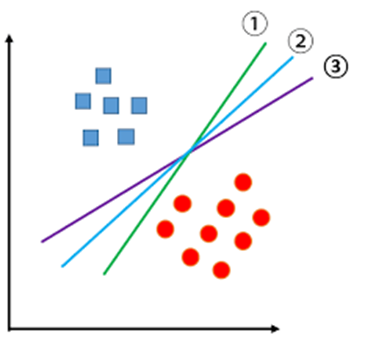
1-3. 최대 마진 분류기(Maximal Margin Classifier)
훈련 관측치들로부터 가장 멀리 떨어진 분리 초평면인 최대 마진 초평면을 선택해야 한다. 각각의 훈련 관측치에서 주어진 초평면까지의 수직거리를 계산하고, 이 값에 따라 최적의 초평면을 선택하게 된다.
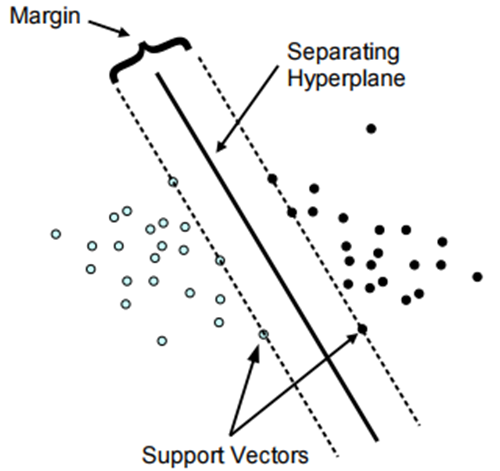
📍 왜 마진이 커야할까요?
Margin이 작은 값이라고 가정해보자. 그렇다면 조그만 변화에도 관측값들의 결과값이 달라질 수도 있고, 이는 곧 완벽한 분류를 못함을 의미한다. 때문에 Margin이 큰 값을 가질수록 관측값들을 완벽하게 분류할 수 있다.
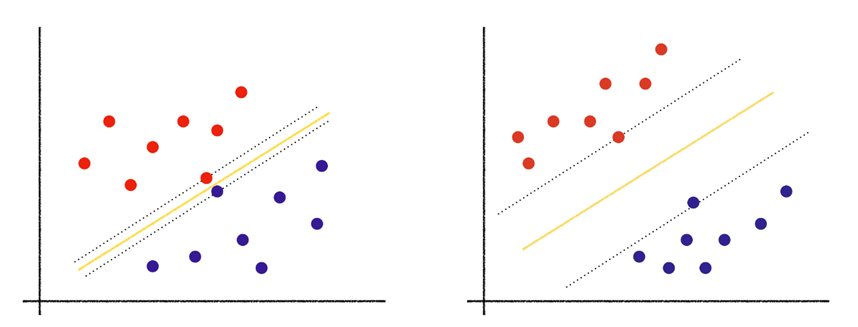최대 마진 초평면은 서포트 벡터에 따라 변하지만, 다른 관측치들에 의해서 변경되지는 않는다.
최대 마진 분류기는 분리 초평면이 존재한다면 분류를 수행하기 위해 매우 좋은 방법이다. 하지만 어떤 데이터의 경우 초평면이 존재하지 않을 수 있고, 따라서 최대 마진 분류기 또한 존재할 수 없다(아래 그림 참고). 이를 해결하기 위해, 소프트 마진(soft margin)이라는 것을 사용하는데, 이는 약간의 오류를 허용함으로써 관찰값들을 분류하는 것이다.
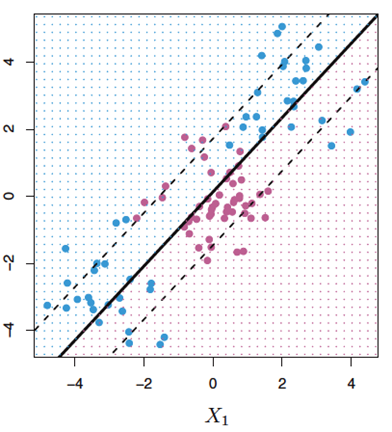
<초평면에 의해 분류가 잘 되지 않은 데이터> -> Hard margin svm로는 어려움.
1-4-1. 서포트 벡터 분류기(Support Vector Classifier)
⚫ 소프트마진(sofr margine)을 사용하여 약간의 오류를 허용하면서 관찰값을 분류하는 것.
서포트 벡터 분류기는 최대 마진 분류기를 확장한 개념으로 몇몇 훈련 관측치들을 잘못 분류하더라도 나머지 관측치들을 더 잘 분류할 수 있는 방법이다. 모든 관측치가 초평면뿐만 아니라 마진의 올바른 쪽에 있도록 가능한 가장 큰 마진을 찾는 대신에, 일부 관측치들은 마진의 옳지 않은 쪽에 있거나 심지어는 초평면의 옳지 않은 쪽에 있을 수 있도록 허용된다(이때 마진이 소프트하다고 하는 이유는 일부 훈련 관측치들이 마진에 위반되서 분류되기 때문이다)
즉, 어느정도의 오류를 인정한다.
1-4-2. Outlier 처리
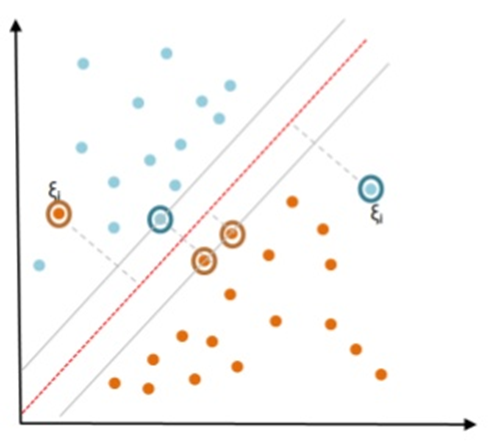
약간의 오류를 허용함으로써 분류를 수행하면 과적합(Overfitting)도 방지할 수 있다. 즉, 모든 데이터를 정확히 분류하고자 하는 초평면을 찾아낸다면, 그 초평면은 해당 데이터에서만 높은 정확도를 가져오는 과적합(Overfitting)의 위험이 있다. 하지만 위와 같이 약간의 오류를 허용해 준다면 어느 정도의 과적합은 방지될 수 있다.
1-4-3. 서포트 벡터 머신(Suppotrt Vector Machine)
서포트 벡터 분류기를 확장하여 비선형의 클래스 경계를 수용하는 분류방법 중 하나다. 즉, 선형분류기를 비선형 구조로 변경해서 관측값들을 분류하는 것이다.
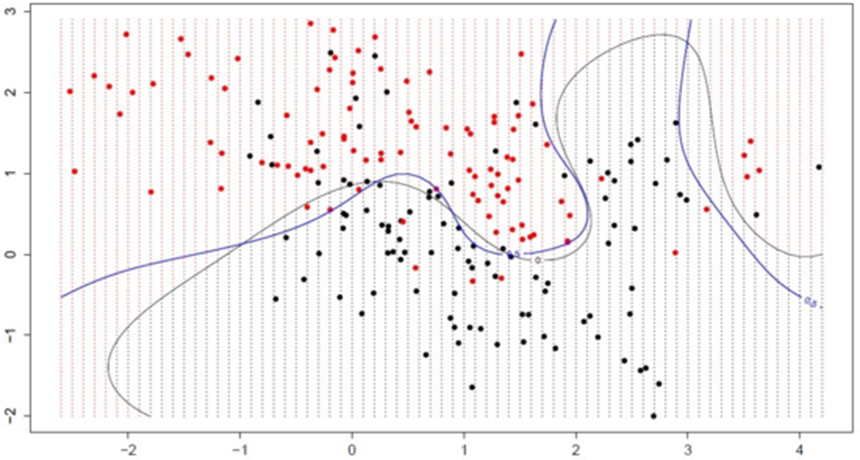서포트 벡터 머신(Support Vector Machine)은 커널(Kernels)을 사용하여 특정한 방식으로 변수공간을 확장한 결과이다.
1-4-4. Hard margin svm
정반대로, 한 치의 오류도 허용하지 않는 분류모델.
◼ 엄격한 분류 규칙
:하드 마진 SVM은 훈련 데이터를 완벽하게 분류하는 결정 경계를 찾는다. 이는 모든 훈련 데이터가 마진의 올바른 쪽에 위치해야 한다는 것을 의미한다.
◼ 이상치에 대한 민감성
: 하드 마진 방식은 데이터 세트 내의 이상치나 노이즈에 매우 민감하다. 하나의 이상치도 마진을 크게 변경할 수 있으며, 이는 결정 경계의 형태와 위치에 큰 영향을 미친다.
◼ 과적합(Overfitting)의 위험
: 이상치에 대한 민감성으로 인해, 하드 마진 SVM은 특히 작은 노이즈가 있는 데이터셋이나 이상치가 존재하는 데이터셋에서 과적합이 발생하기 쉽다. 과적합이 발생하면, 모델은 훈련 데이터에 대해서는 높은 정확도를 보이지만, 새로운 또는 보이지 않은 데이터에 대해서는 일반화 성능이 떨어지게 된다.
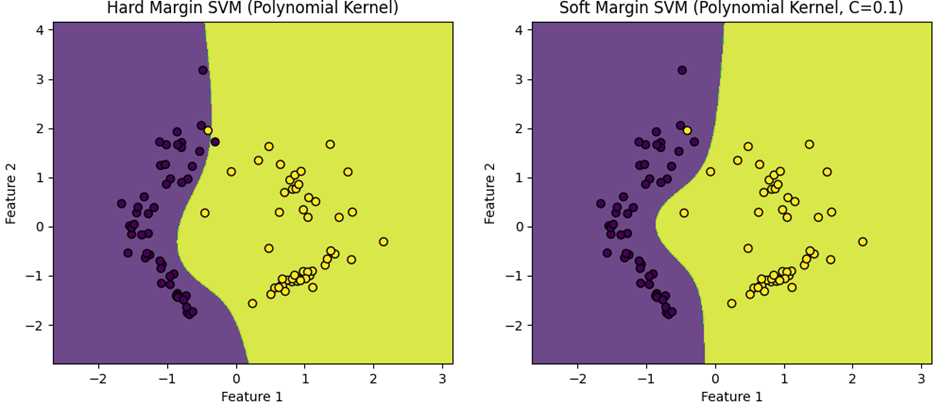참조 : https://www.globalsino.com/ICs/page3808.html
1-5-1. 주요 파라미터 튜닝
A. Cost : 얼만큼 오차를 허용할 것인지에 대한 파라미터
일정 수준의 오류를 허용해 주었기 때문에, SVM에서 중요한 일은 바로 “어느 정도의 오류를 허용해 줄 것인가? 이다.
➢ 이 Cost인자에 적합한 파라미터값을 설정해 주어야지만 높은 정확도를 가져올 수 있다. 결론적으로 Cost가 큰 값을 가지면 margin의 폭은 작아지고, Cost가 작은 값을 가지면 큰 폭의 margin을 가진다.
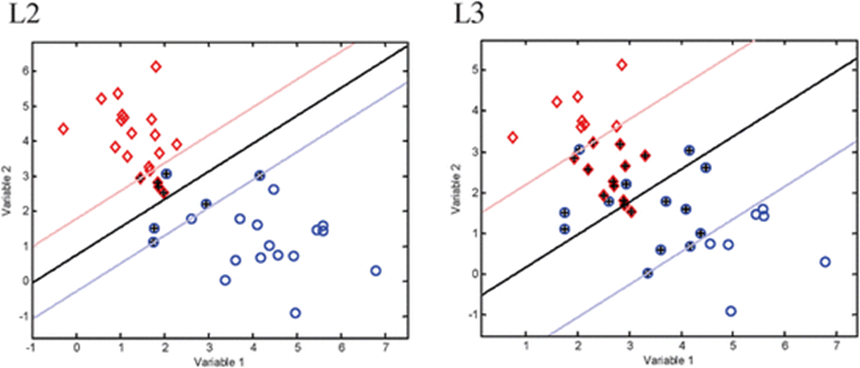<왼쪽: 높은 Cost로 margin의 폭이 적음, 오른쪽: 낮은 Cost로 margin의 폭이 넓음>
B. kernel : kernel 파라미터는 decision boundary의 모양을 선형으로 할지 다항식형으로 할지 등을 결정
- Gamma : 커널(kernel)과 관련이 있는 수치
두 클래스 사이의 결정 경계(Decision Boundary)를 찾는 것이 주 목적이다. SVM은 고차원, 적은 데이터셋, 그리고 분류가 어려운 복잡한 데이터셋에서도 잘 작동하는 것으로 알려져 있다.
reach는 decision boudary의 굴곡에 영향을 주는 데이터의 범위로, Gamma가 작다면 reach가 멀다는 뜻이고, Gamma가 크다면 reach가 좁다는 뜻
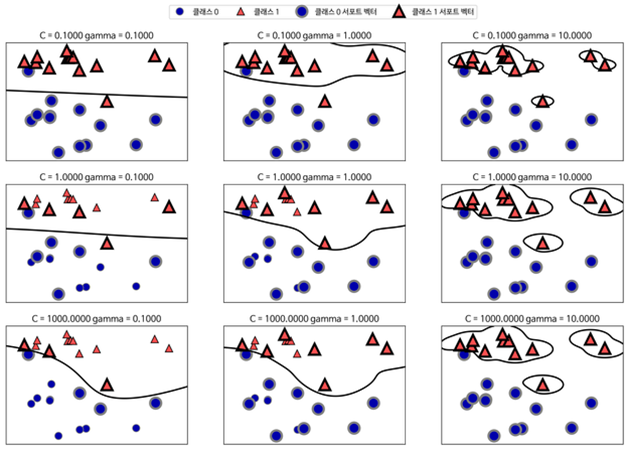
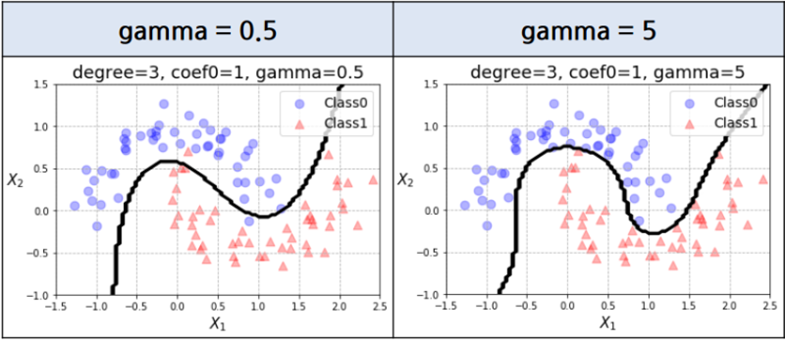
결론적으로 Gamma가 크면 decision boundary는 더 굴곡지고, Gamma가 작으면 decision boundary는 직선에 가깝다.
[실습 결과]
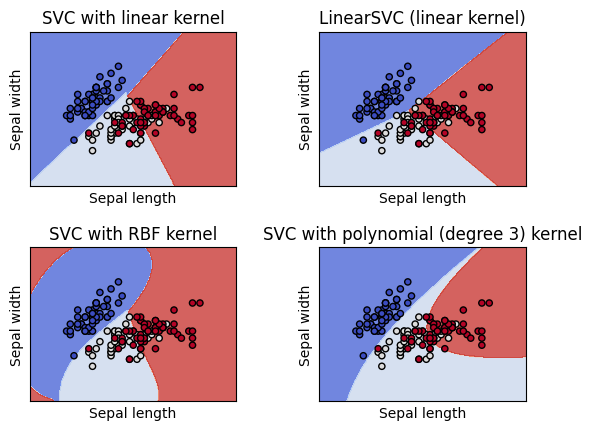
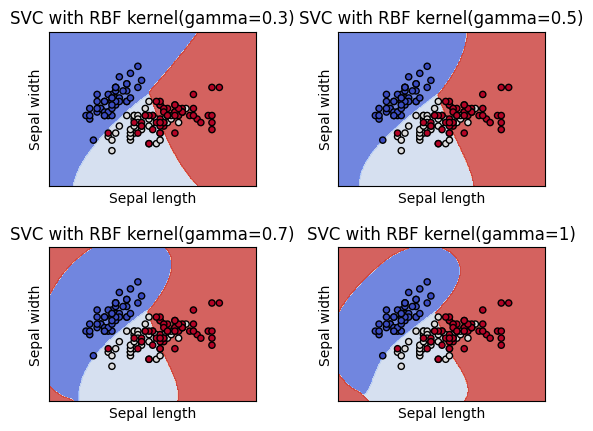
1-5-2. 커널 트릭 (Kernel Trick) - 비선형 SVM
: 데이터의 분류가 어려울 때, 저차원 공간(low dimensional space)을 고차원 공간(high dimensional space)으로 매핑해주는 작업을 커널 트릭(Kernel Trick)
(즉, 먼저 고차원 공간에서의 linear한 해를 구한 뒤 저차원 공간에서의 non linear한 해 를 구하는 것)
배경 - 단순한 데이터 세트의 경우 쉽고 간단하게 선으로 분리가 가능하지만 데이터 세트가 복잡하고 많아지게 되면 하나의 선 또는 면으로 쉽게 분리하기 어려워 진다
참고 : https://www.youtube.com/watch?v=3liCbRZPrZA&t=42s
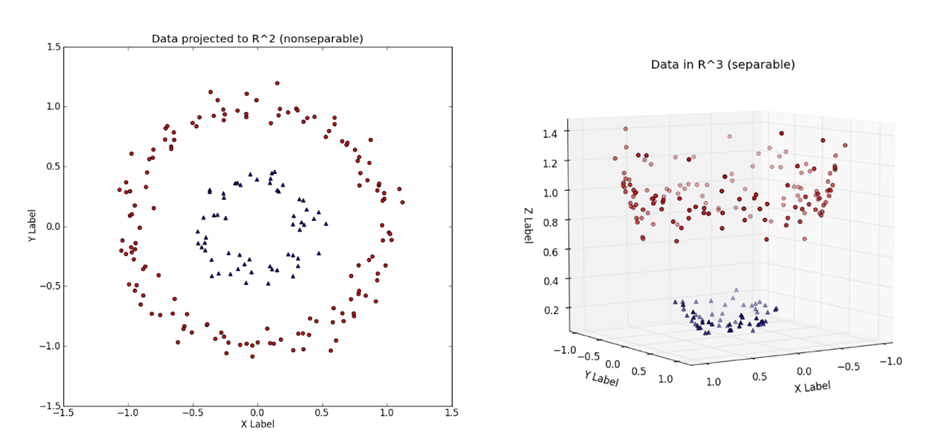
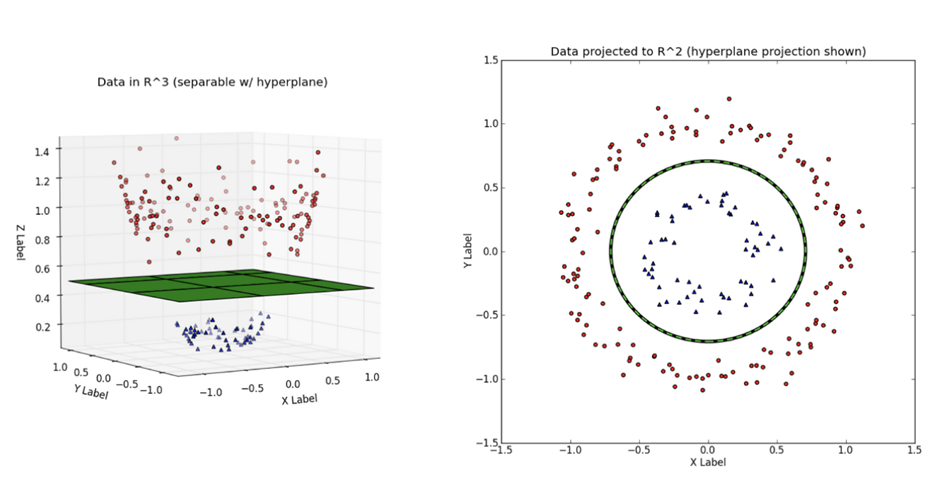
⚫ 커널은 클래스들 사이의 비선형 경계를 수용하기 위해 변수공간을 확장하고자 할 때 사용하는 계산기법. 커널의 차원을 높임으로써 좀 더 다양한 결정경계가 만들어지고 이를 다항식 커널이라 한다.
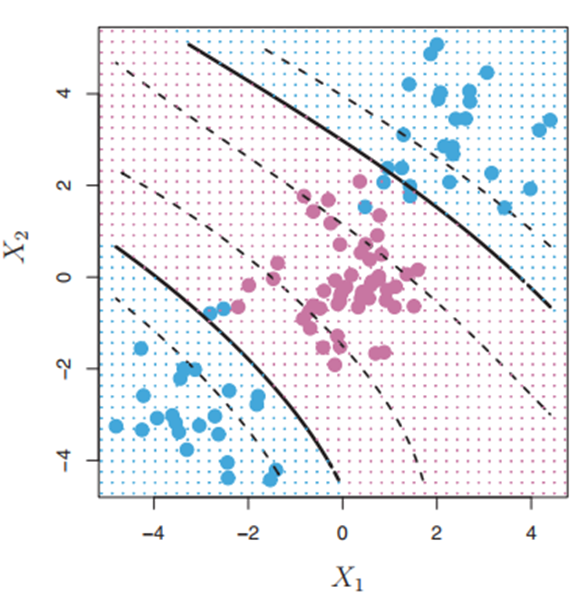
< 🔼 다항식 커널을 가진 서포트 벡터 머신 >
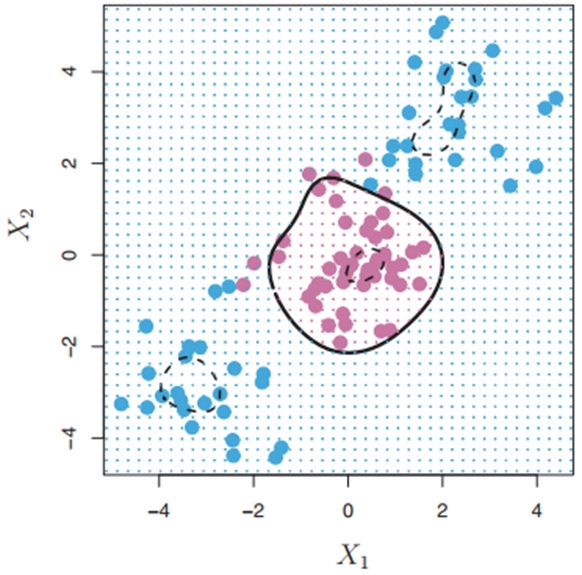
비선형커널 외에도 방사커널(Radial Kernel)이 널리 사용된다. 다음은 방사커널을 가진 SVM이며, 두 클래스가 잘 분류됨을 볼 수 있다.
1-6. 서포트 벡터 머신(Support Vector Machine)에서 분류와 회귀 비교
서포트 벡터 머신은 분류와 회귀 문제에서 모두 사용할 수 있다.
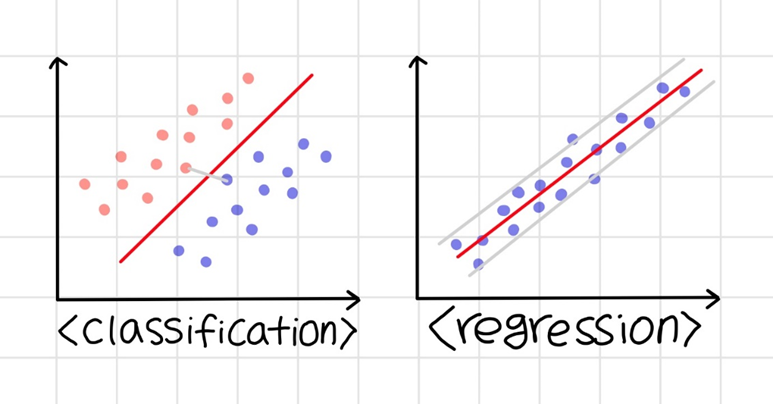
✓ 먼저 분류 문제에 서포트 벡터 머신을 사용할 경우, 지금까지 정리한 것처럼 각 집단의 경계에 인접해 있는 데이터들의 거리가 가장 멀어지게 폭(마진)을 설정하여 마진의 가운데를 결정 경계로 잡는다. 이러한 분류의 경우, 두 집단 사이의 거리(마진)가 클수록 좋기 때문에 소프트 마진을 사용하는 것이 좋다.
✓ 반면 회귀 문제로 서포트 벡터 머신을 사용하는 경우에는 데이터들을 대표하는 직선을 만드는 것이 목표이기 때문에 데이터들을 아우를 수 있게 마진을 잡고 그 중앙에 회귀선을 그어주는 방식으로 작동한다. 따라서 마진이 좁을수록 데이터들을 대표할 수 있는 회귀선을 잘 만들 수 있기 때문에 하드 마진을 사용하는 것이 좋다.
1-7. 사용 사례
SVM은 이미지 분류, 텍스트 분류, 바이오인포매틱스(단백질 분류, 유전자 분류 등), 손글씨 인식 등 다양한 분야에서 뛰어난 성능을 보여준다. (머신러닝의 최고봉이라고 불림) 특히, 데이터의 특성이 명확히 구분되지 않고, 데이터 포인트의 수가 변수의 수보다 적은 경우에 잘 작동하는 경향이 있다. SVM의 핵심은 적절한 커널 함수의 선택과 파라미터 튜닝에 있다
* Reference
https://m.blog.naver.com/winddori2002/221662413641
https://blog.naver.com/tjdudwo93/221051481147
https://bkshin.tistory.com/entry/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-2%EC%84%9C%ED%8F%AC%ED%8A%B8-%EB%B2%A1%ED%84%B0-%EB%A8%B8%EC%8B%A0-SVM
https://velog.io/@shlee0125/%EB%A8%B8%EC%8B%A0%EB%9F%AC%EB%8B%9D-%EC%A0%95%EB%A6%AC-Support-Vector-Machine-05.-Why-does-SVM-maximize-margin
https://www.globalsino.com/ICs/page3808.html
https://blog.naver.com/winddori2002/221667083964
https://todayisbetterthanyesterday.tistory.com/32
https://velog.io/@dxstyblxe/Python-%EC%84%9C%ED%8F%AC%ED%8A%B8-%EB%B2%A1%ED%84%B0-%EB%A8%B8%EC%8B%A0-SVM-SVC-SVR-%EC%BD%94%EB%93%9C-%EC%8B%A4%EC%8A%B5%ED%95%98%EA%B8%B0
https://liveyourit.tistory.com/62
https://blog.naver.com/slykid/221630584607
