Field-aware Factorization Machines for CTR Prediction(2)

DONGJIN IM·2022년 6월 13일

논문

논문 리뷰

목록 보기

8/8

Sparse Data란??

차원/전체 공간에 비해 데이터가 있는 공간은 매우 적은 데이터

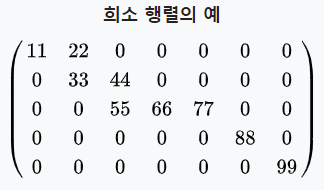
출처 : Wikipedia

위 행렬을 보면 차원에 비해 0의 개수가 많이 보인다. 따라서 Sparse Matrix가 되고, 이런 데이터가 활용된다면 이 데이터를 Sparse Data라고 한다.

이전 Section에서 말했듯, 추천 시스템의 Rating Matrix는 희소 행렬인 경우가 많고, Data 자체도 Sparse Data일 확률이 매우 높다.

Intoduction

Optimization Problem

min_w \frac{\lambda}{2}||w||^2_2 + \sum_{i=1}^mlog(1 + e^{-y_i\phi_{LM}(w,x_i)})

w : Model
m개의 Instance들 $(y_i, x_i)$ 가 존재하는 Dataset이 주어짐
$y_i$ : Label
$x_i$ : n-dimensional Feature Vector
$\phi_{LM}(w,x)= w\cdot x$
- Linear Model으로 가정하기 때문에 위와 같이 생각함
$\lambda$ : Regularization Parameter

Feature Conjunctions

CTR Prediction에 있어 Feature Conjunctions를 이해하는 것은 중요함
- (1)에서 정리한 Feature Vector를 생각하자
Simple Linear Regression과 같은 간단한 모델은 Feature Conjunctions를 이해하지 못함
- 2개의 Feature를 동시에 고려해야 하는데, Linear Model은 2개의 Feature를 동시에 고려할 수 없음
degree-2 Polynomial Mappings(Poly2) Model
- 각각의 Feature Conjunction을 위한 전용 가중치를 학습하는 방식
- 즉, $x_ix_j$ 연산을 위한 Matrix인 $W$ 를 하나 더 형성
FMs(Factorization Machines)
- 2개의 Latent Vector들의 내적으로 Factorizing함으로써 학습
- Factorized Parameterization 활용
  - $x_ix_j$ 연산을 위해 Poly2에서 활용하는 전용 가중치를 분해한 뒤, 여기에서 나온 $v_i, v_j$ 를 내적한 값을 활용

FFMs

PITF : Personalized Tag 추천을 위해 나온 FMs의 변형 모델
FFMs
- KDD Cup2020에서 Team Opera Solutions가 Generalization of PITF로써 발표한 Model
- 원래 이름은 "factor model'이지만, 너무 일반적이고 Factorization machine과 혼동하기 쉬워 이 논문에선 FFMs라고 말함
PITF는 User, Item, Tag를 포함한 3가지 Special Field를 고려하지만, FFMs는 더욱 일반적인 모델
FFMs 주요 특징
- Optimization Probelm 해결을 위해 SG(Stochastic Gradient)를 활용
  - Overfitting을 막기 위해 1 Epoch만 학습
- FFMs는 비교한 6개 모델 중 가장 성능이 좋았음

논문 목표 및 기여

목표 : CTR Prediction 해결의 효과적 접근 방식인 FFMs를 구체적으로 확립하는 것
FFMs가 실제로 효율적인지 증명
- FFMs 효과가 좋아보인다고 말한 것은 FFMs가 적용된 연구에서만 주장되었음
- 실제로 효율적인지를 증명하기 위해 우리의 Major Model로써 FFMs를 활용하여 2개의 World-wide CTR prediction 대회에서 수상
왜 FFMs가 Poly2와 FMs보다 좋은지 "이론적으로" 설명하고, Accuracy 및 학습 시간 측면의 장점을 보여주기 위한 비교 실험을 진행
효율적인 Parallel Optimization Algorithm 및 Overfitting 방지를 위한 Early-Stopping 기법에 대한 기술 제안
FFMs를 공적으로 활용 가능하도록 Open Source Software로 발표함

Poly2 and FM

Poly2

Degree-2 Polynomial Mapping은 Feature Conjunction의 정보를 효율적으로 뽑아낼 수 있다.

또한, Degree-2 Mappings의 Explicit Form에 Linear Model을 적용시켰을 때 학습 및 Test time이 Kernel Methods를 활용했을 때보다 더욱 빨라졌음을 보였다.

이런 접근법으로 각각의 Feature Pair를 위한 가중치를 학습하면 되는 것이다.

\phi_{Poly2}(w, x) = \sum^n_{j_1=1}\sum^n_{j_2=j_1+1}w_{h(j_1,j_2)}x_{j_1}x_{j_2}

$h(j_1,j_2)$ : $j_1, j_2$ 를 자연수로 Encoding하는 함수
n : Feature Dimension
Complexity : $O(\bar{n}^2)$
- $\bar{n}$ : Instance 1개 당 non-zero elements의 평균 개수

Poly2에서 $h(j_1, j_2)$ 모든 Pair가 새로운 Feature Pair로 고려된다.
(즉, 모든 h값이 학습에 활용된다)
이는 매우 $O(n^2)$ 의 Complexity를 고려할 때 n이 너무 커져 비실용적이다.

VW에서는 $j_1, j_2$ 를 Hashing함으로써 이 문제를 어느정도 해결했다.

h(j_1, j_2) = (\frac{1}{2}(j_1+j_2)(j_1+j_2+1) + j_2) mod B

B : Model size. User-specified Parameter

FMs

FMs는 각각의 Feature에 대한 Latent Vector를 학습한다.
( $v_i$ 를 의미하는 것)

Latent Vector는 k개의 Latent Factor를 포함하는데, 이 때 k는 User-specified Parameter이다.
Feature Conjunction의 효과는 2개의 Latent Vector의 내적에 의해 모델링된다.

\phi_{FM}(w, x) = \sum^n_{j_1=1}\sum^n_{j_2=j_1+1}(w_{j_1}\cdot w_{j_2})x_{j_1}x_{j_2}

$w_{j_1}\cdot w_{j_2}$ : Feature에 대응하는 Latent Vector의 내적
Computing cost : $O(\bar{n}^2k)$
- 이유 : Variable 개수는 n X k이다. 해당 연산을 n번 수행해야 모든 연산이 수행되기 때문에 cost는 $O(\bar{n}^2k)$ 가 된다.

하지만, 이 식을 아래와 같이 수정하여 활용 할 수 있다.

\phi_{FM}(w, x) = \frac{1}{2}\sum^n_{j=1}(s - w_jx_j)\cdot w_jx_j

$s = \sum_{j'=1}^nw_{j'}x_{j'}$

이 경우 Complexity가 $O(\bar{n}k)$ 까지 줄어든다.

FMs와 Poly2 비교

Dataset이 Sparse할 때 Poly2보다 FMs가 훨씬 좋은 성능을 낸다.

Poly2에서는 2개의 쌍에 대해 학습이 진행되지만, FMs에서는 다른 Pair들로부터 학습된 Feature의 내적값을 활용하므로 더 정확한 결과를 도출한다.
Poly2에서는 모든 Pair를 독립적으로 보기 때문에 모든 값이 학습에 적용된다. 하지만 FMs에서는 다른 pair들로부터 학습된 것도 영향을 주기 때문에 조금의 보정이 들어가 더 정확해진다.
또한, Poly2에서는 0으로 예측한 것은 학습 데이터로 삼지 않지만(영향이 적지만) FMs에서는 0 또한 학습 데이터로 활용하기 때문에 더 좋을 수밖에 없다.

FFM

0. FFM 아이디어

FFM이란?

FFM은 Personalized tag가 존재하는 추천 시스템을 위해 제안된 PITF로부터 파생되었다.
PIFT는 User, Item, Tag를 포함한 3개의 Field를 가정했고, 분리된 Latent Space에서 (User, Item), (User, Tag), (Item, Tag)로 Factorize하였고, FFM은 조금 더 이런 Field를 일반화시켜 적용한 모델이다.

하지만 이런 정의는 "추천 시스템"에 목적을 둔 정의이며, CTR Prediction에 있어서는 상세 설명이 부족하다.
따라서, 이 논문에서 FFM에 대한 포괄적인 논의를 진행해 볼 것이다.

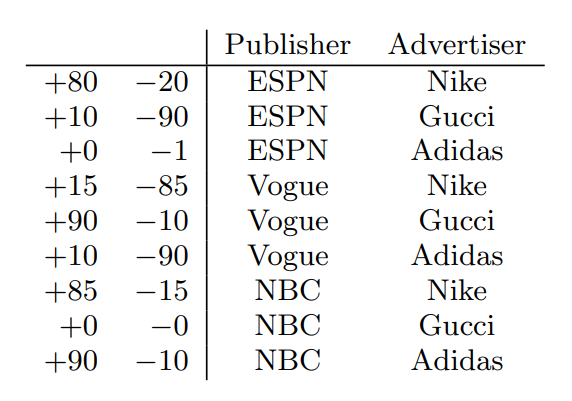
출처 : Field-aware Factorization Machines for CTR Prediction(paper)

위 사진에서 {ESPN, Vogue, NBC}는 Publisher라는 Field에 속한다고 말할 수 있다.
FFM은 이렇게 Field를 형성하여 활용하는 FM의 변형 모델인 것이다.

FFM 동작 원리

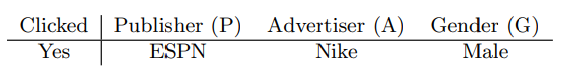
출처 : Field-aware Factorization Machines for CTR Prediction(paper)

위와 같은 상황이 주어졌다고 가정하고, 위에서 설명했던 $\phi_{FM}$ 에 대해 생각해보자.

\phi_{FM}(w, x) = \sum^n_{j_1=1}\sum^n_{j_2=j_1+1}(w_{j_1}\cdot w_{j_2})x_{j_1}x_{j_2}

예시 상황을 수식에 대입시켜보면 $\phi_{FM}$ 은 아래와 같다

w_{ESPN} \cdot w_{Nike} + w_{ESPN} \cdot w_{Male} + w_{Nike} \cdot w_{Male}

FM에서는 모든 Feature는 다른 Feature들과의 Latent Effect를 학습하기 위해 오직 하나의 Latent Vector만을 가진다.
위 예시에서 $w_{ESPN}$ 은 Nike와 Male과의 Latent Effect를 학습하는 것이다.
하지만, 중요한 점은 Nike와 Male의 Field는 다르다는 점이다.
Field가 다르기 때문에 (ESPN, Nike)와 (ESPN, Male) 관계에서 활용된 $w_{ESPN}$ 은 다를 확률이 매우 높다

하지만, 위 예시에서 보듯 $w_{ESPN}$ 은 1개만 존재하므로, 하나의 벡터가 2개(혹은 그 이상)의 관계를 모두 표현할 수 있어야 되는 것이다.
1개의 벡터가 여러 종류의 Field 영향을 모두 표현하기엔 어려움이 존재한다.

FFM은 이런 문제를 해결했다.

\phi_{FFM}(w,x) = w_{ESPN, A} \cdot w_{Nike, P} + w_{ESPN, G} \cdot w_{Male, P} + w_{Nike, G} \cdot w_{Male, A}

위 식과는 다르게 $w_{ESPN, A}$ 와 같이 뒤에 "A"라는 값이 추가되었음을 알 수 있다.
이 뒤에 붙은 A는 내적 연산을 수행하는 상대의 "Field"를 표현한다.
(Nike는 Advertiser Field에 속하므로, "A"를 붙여줌)

즉, FFM은 각각의 Latent Vector가 오직 "특정 Field"와 관련된 부분에 대해서만 학습이 진행되면 되기 때문에 FM과 비교해 보았을 때 k값이 현저히 작다.

$\phi_{FFM}$ 을 일반화시키면 아래와 같다
$\phi_{FM}(w, x) = \sum^n_{j_1=1}\sum^n_{j_2=j_1+1}(w_{j_1, f_2}\cdot w_{j_2, f_1})x_{j_1}x_{j_2}$
- $f_1(f_2)$ : $j_1(j_2)$ 가 속하는 Field
- Complexity : $O(\bar{n}^2k)$
- Number of Variables : nfk
  - f : Field 개수

1. Solving the Optimization Problem

FFM의 Optimization Problem
$min_w \frac{\lambda}{2}||w||^2_2 + \sum_{i=1}^mlog(1 + e^{-y_i\phi_{FFM}(w,x_i)})$
- Simple Logistic Regression 최적화에서 $\phi_{LM}$ 을 $\phi_{FFM}$ 으로 바꿔주기만 하면 됨

우리는 실험에서 SG(Stochastic Gradient)를 활용하였고, Matrix Factorization에서 효과적인 AdaGrad를 활용했다

SG의 Step마다 Data Point (y,x)는 $w_{j_1,f_2}, w_{j_2,f_1}$ 을 업데이트하기 위해 추출된다.

데이터 x는 Sparse하기 때문에 이 논문에선 non-zero value만 Update할 것이다.

Sub Gradient 수식은 아래와 같다.

g_{j_1, f_2} \equiv \triangledown_{w_{j_1,f_2}}f(w) = \lambda\cdot w_{j_1,f_2} + \kappa \cdot w_{j_2,f_1}x_{j_1}x_{j_2}\newline g_{j_2, f_1} \equiv \triangledown_{w_{j_2,f_1}}f(w) = \lambda\cdot w_{j_2,f_1} + \kappa \cdot w_{j_1,f_2}x_{j_1}x_{j_2}\newline

$where$

\kappa = \frac{\partial log(1 + e^{-y\phi_{FFM}(w,x)})}{\partial\phi_{FFM}(w,x)} = \frac{-y}{1 + e^{y\phi_{FFM}(w,x)}}

모든 Coordinate d = 1,...,k에서 Squared Gradient의 합은 아래와 같이 계산된다.

(G_{j_1, f_2})_d \leftarrow (G_{j_1, f_2})_d + (g_{j_1,f_2})^2_d

(G_{j_2, f_1})_d \leftarrow (G_{j_2, f_1})_d + (g_{j_2,f_1})^2_d

Adagrad에서는 이전까지의 Gradient값을 제곱하여 이전 $G_t$ 에 더함으로써 Sum of Gradient Squres를 구함
https://velog.io/@idj7183/Optimizer-%EB%B0%9C%EC%A0%84-%EC%97%AD%EC%82%AC

최종적으로 이렇게 구한 $G_t$ 를 활용하여 Adagrad 방법을 통해 Update가 가능해진다.

(w_{j_1, f_2})_d \leftarrow (w_{j_1, f_2})_d - \frac{\eta}{\sqrt{(G_{j_1,f_2})_d}}(g_{j_1,f_2})_d

(w_{j_2, f_1})_d \leftarrow (w_{j_2, f_1})_d - \frac{\eta}{\sqrt{(G_{j_2,f_1})_d}}(g_{j_2,f_1})_d

$\eta$ : Learning Rate
- User-specified Parameter
초기값
- $w$ : [0, $1 /\sqrt{k}$ ]의 Uniform Distribution에서 랜덤한 값으로 초기화 됨
- $G$ : $\sqrt{(G_{j_1,f_2})_d}^{-\frac{1}{2}}$ 이 너무 커지지는 현상을 막기 위해 1로 설정

경험적으로 각 Instance를 Unit Length를 가지도록 Normalize해주는 것이 테스트 정확도를 향상시키고 매개 변수에 민감하지 않게 된다는 것을 찾았다

Algorithm 설명

2. Parallelization on Shared-Memory Systems

이 실험에서는 SG를 위한 많은 Parallelization 접근법들 중 $H_{OG-WILD!}$ 라는 Locking 없이 독립적으로 수행되는 Thread를 허락하는 기법을 활용했다.

Algorithm에서 Line3의 for문이 Parallelized됨

3. Adding Field Information

널리 활용되는 LIBSVM Data Format은 아래와 같다.
label feat1:val feat2:val2 ...

(ex) Clicked Publisher-ESPN:1 Advertiser-Nike:1 Gender-Male:1 ...
- val1 : 해당 Feture에 대한 비중이라고 생각하면 편할 것 같다.
  - Publisher, Advertiser, Gender같은 경우 One-hot Vector이므로 1 혹은 0의 값을 가짐
  - 1 ~ 5점을 준 영화의 % 등의 값을 표시할 때 0.2 등으로 설정 가능
  - LIBVSM 포맷에서 val = 0인 값은 저장되지 않음

하지만 FFM에서는 우리는 이 형식을 확장하여 활용했다.
label field1:feat1:val1 field2:feat2:val2

(ex) Clicked Publisher:Publisher-ESPN:1 Advertiser:Advertiser-Nike:1 ...

즉, 각각의 Feature에 대해 일치하는 Field를 할당할 것이다.
하지만 이 작업은 특정 Feature에 대해선 쉬운 작업이지만 아닐 수도 있다.
따라서 3가지 종류의 Feature 관점에서 논의해보겠다.

Categorical Features

선형 모델에서는 Categorical Feature를 여러 개의 Binary Feature로 변형하는 것이 일반적이다.

위에서 설명했듯 LIBSVM 포맷에서는 0의 값은 저장되지 않으므로 모든 Categorical Feature들은 Binary Feature로 변형 가능하다.
따라서, One-hot Vector처럼 Binary Feature로 표현 가능하다.

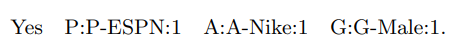
Numerical Features

Conference에서 논문이 통과될지에 대한 데이터를 예시로 들어보자.
우리는 AR(수용 확률), Hidx(저자 수), Cite(인용수) 총 3개 Feature가 존재한다.

첫번째 방법은 Dummy Field를 활용하여 아래와 같이 데이터를 만드는 것이다.

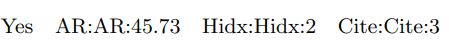
Field = Feature가 되도록 설정했음

하지만 Dummy Field는 단순한 Feature의 중복이므로 유용하지 않다.

두 번째 방법은 Feature를 Field에 넣고 기존의 실수 값(Value)을 이산화(Discretize)하여 Feature로 만들어주는 것이다.
이후, Categorical Features와 동일하게 Binary Feature로 생각하여 0 혹은 1의 값을 넣어주는 방법이다.

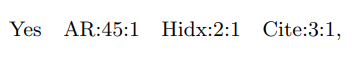
여러 가지 방법으로 이산화 할 수 있다.
하지만, 어떤 방법이든 어느 정도의 정보 손실을 감수해야 하며, Best Discretization Setting을 찾기가 어렵다는 단점이 존재한다.

Single-Field Features

어떤 Dataset에서는 모든 Feature가 Single Field를 가지고 Feature에 대해 Field를 지정해주는 것이 무의미한 경우도 있다.
특히 NLP 같은 분야에서 이런 현상이 두드러진다.

위 예시를 보면 Sentence라는 Field로 밖에 묶을 수 없음을 알 수 있다.
Reader들은 Numerical Feature에서 수행했던 것처럼 Dummy Field를 할당하는 것을 생각할 수 있으나 이 경우 f(feature 개수)가 너무 커져 굉장히 비실용적이다.

FFM의 모델 크기는 $O(nfk)$ 이고, 만약 dummy field를 활용하면 f=n이므로 n이 대부분의 경우 매우 크다는 것을 고려할 때 f도 매우 커지게 된다.

Experiments

0. Section 설명

Section 4.1 : 실험 Setting에 대한 상세 설명
Section 4.2 : Parameter 영향
- LM과 Poly2와는 다르게 FFM은 Epoch의 영향을 크게 받음
Section 4.3 : Early Stopping Trick
Section 4.4 : Parallelization 활용을 통한 Speedup
- 같은 SG Method로 수행함
- Accuracy와 Training Time을 공정히 비교할 수 있게 됨
Section 4.5, 4.6 : 여러 가지 Data에 대하여 성능 비교

1. Experiment Settings

Datasets

먼저 Kaggle 대회의 Criterio와 Avazu 2개의 CTR Dataset으로 실험하였다
(4.6에서 더 많은 데이터로 실험해 봄)

Hash Trick이 $10^6$ Features를 형성하도록 적용했다.

Test set의 Label들이 공적으로 사용 불가하여 우리는 활용 가능한 Data를 Train/Validation으로 나누어서 활용했다.

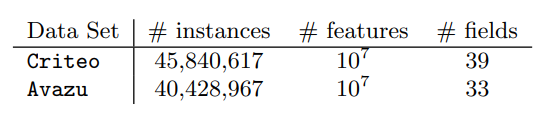
용어 설명
- Va : Validation set
- Tr : 새로운 Training Set
  - Original Training Set에서 Validation Set을 제외한 것
- TrVa : Original Training Set
- Te : Original Test set
  - Label은 발표되지 않음
  - Test set으로 Overfitting되는 것을 막기 위해 Public Set과 Private Set으로 나눠져있다.
- 활용 예시 : CriteoVa - Criteo의 Validation Set

Platform

Linux Workstation
12개의 Physical Core
- 2개의 Intel Xeon E5-2620GHz Processor
- 128GB Memory

Evaluation

Evaluation Criterion을 위해 Logistic Loss를 아래와 같이 지정했다.

logloss = \frac{1}{m}\sum_{i=1}^mlog(1+e^{-y_i\phi(w,x_i)})

m : Instance 숫자
$\phi$ : Model에 대응되는 함수

Implementation

LM, Poly2, FM, FFM 모두 C++로 코드를 짰다.
FM과 FFM은 내적 계산을 빠르게 하기 위해 SSE instruction을 활용했다.

실험 시 몇몇 Dataset에 대한 성능을 올리기 위하여 Linear Term과 Bias Term이 포함했다.
이 Term들은 Harmful하지는 않다고 생각하므로 일반적으로 많이 활용하는 것이 좋을 것 같다.

2. Impact of Parameters

k에 대한 비교

k : Latent Factor 개수
- Logloss에 큰 영향을 끼치지는 않음

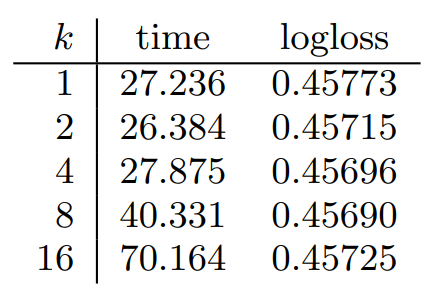
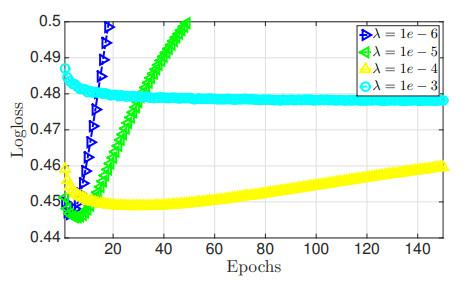
$\lambda$ 에 대한 비교

$\lambda$ : Regularization Parameter
- 매우 컸을 때 좋은 성능을 내지 못함
- 매우 작았을 때 좋은 결과는 냈지만 쉽게 Overfitting됨
  - Training Logloss는 지속적으로 감소하는 것을 볼 때 Overfitting이라고 인지 가능

$\eta$ 에 대한 비교

$\eta$ : Learning Rate
- 작을 경우 FFM Model은 최고 성능을 천천히 냄
- 커질 경우 빠르게 Logloss를 감소시키지만 Overfitting이 발생한다.

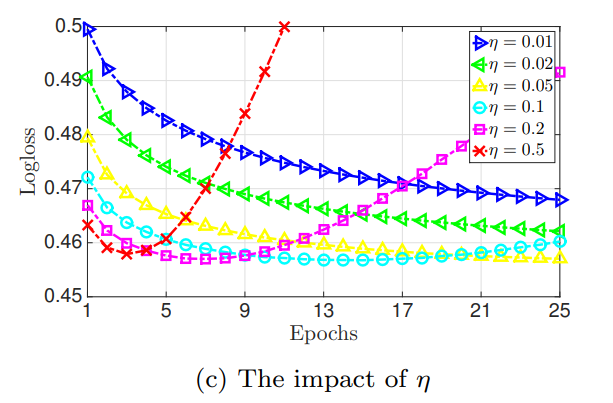
$\lambda$ 와 $\eta$ 실험 그래프를 보았을 때 Early Stopping의 필요성이 존재했다.

3. Early Stopping

논문 실험에서 활용한 Early Stopping 전략은 아래와 같다.

Data를 Train / Validation Set으로 나눈다.
Epoch이 끝날 때마다 Validation Set을 활용하여 Loss를 계산한다.
Loss가 위로 가면(Overfitting이 된다고 판단되면) Epoch 숫자를 기록하고 멈추거나 4번으로 간다
필요하면 Full Dataset과 3번에서 기록한 Epoch으로 모델을 재학습한다.

Logloss는 Epoch 숫자에 민감하기 떄문에 Early Stopping을 적용하기 어려웠다.
특히 Best Epoch이 Test set에서의 최고 Epoch이 아닐 수도 있다는 특징도 존재한다.

Lazy Update나 ALS-based Optiization method같은 Overfitting 방지 기법도 활용했지만 결과가 그렇게 좋진 않았다.

4. Speedup

SG Parallelization이 유사한 Convergence Behaviour를 가진다는 것을 알 수 있었다.

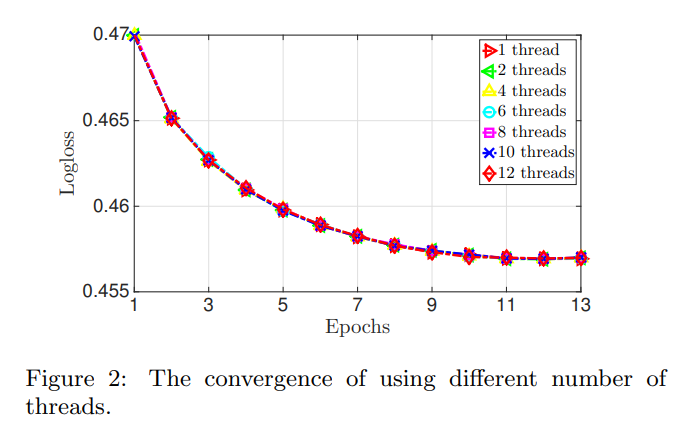
Logloss 측면에서 성능 저하가 없음을 알 수 있음

Speedup = \frac{Running time of one epoch with a singe Thread}{Running time of one epoch with multiple hreads}

하지만 많은 Thread가 활용되면 Speedup이 크게 증가하지 않음을 알 수 있었다.

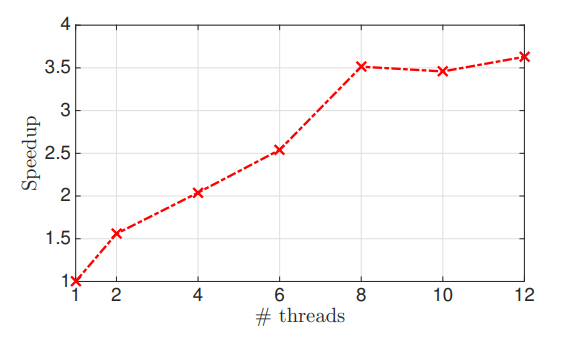
2개 이상의 Thread가 동일한 메모리 주소로 접근을 시도하면 1개의 Thread는 기다려야 하는데, 이런 종류의 충돌은 더 많은 Thread가 활용될 때 더 많이 발생하여 속도 향상을 저하한다.

5. Comparison with LMs, Poly2, and FMs on Two CTR Competition Data Sets

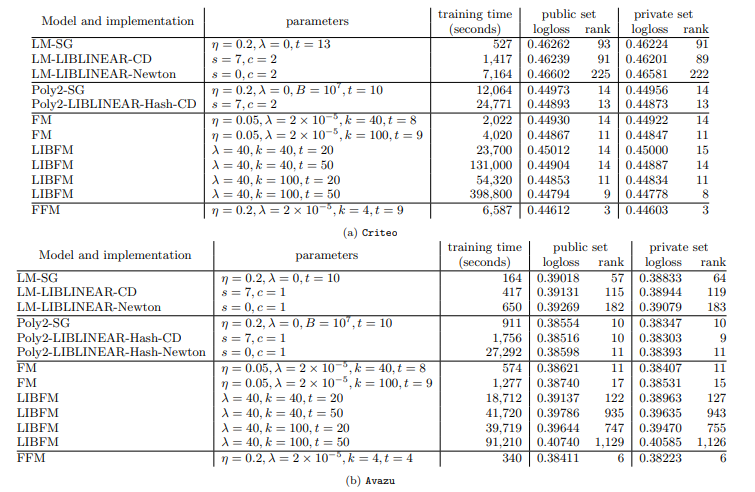
공정한 비교를 위해 동일한 SG Method를 활용했고, LIBLINEAR과 LIBFM 2개의 SOTA Package와 비교해 볼 것이다.

FFM은 다른 모델보다 Logloss 측면에서 뛰어났지만 다른 모델보다 더 긴 학습 시간이 요구되었다.
LM은 다른 모델보다 Logloss 자체는 높았으나 학습 시간은 빨랐다.
이를 통해 Logloss와 학습 시간은 반비례 관계를 가짐을 알 수 있었다.(Logloss가 높으면 학습 시간이 짧음)
Poly2는 모든 모델 중 가장 느렸고 Computation Cost도 가장 비쌌다.
FM은 Logloss와 학습 시간에 대해 좋은 Balance를 가졌다.

LIBFM의 FM은 Criteo Dataset에 대해 Logloss 측면에서 비슷한 성능을 냈다.
하지만, 우리의 Time이 더 빨랐고, 3가지 이유 중 하나라고 생각했다.
1. ALS Algorithm이 SG 보다 복잡하다.
2. Adaptive Learning Rate strategy를 활용하여 이점을 가져왔다.
3. SSE Instruction이 내적 계산을 가속시켜 속도가 빨라졌다.

Logistic Regression은 Convex Probelm이므로 LM이나 Poly2의 경우 3가지 Optimization Method(Newton, SG, CD) 중 어떤 것을 활용하더라도 정확히 동일한 모델을 생성해야 한다 생각했지만, 결과는 살짝 달랐다.

그래서 우리 실험에서 Optimization Method는 정지 조건이 (Convex Problem이라도) 결과 모델 성능에 영향이 있음을 알게 되었다.

6. Comparison on More Data Sets

다른 데이터셋에서도 FFM이 좋은 성능을 보이는지 확인하기 위하여 많은 데이터에 대해 실험해보았다.

Single-field Features Dataset에 대해서는 고려하지 않고 실험
데이터셋 설명
- KDD2010-bridge : Numercial과 Categorical Features를 동시에 포함한 데이터
- KDD2012 : Numerical과 Categorical Features를 동시에 포함한 데이터
  - Target Value인 number of clicks를 Binary Value인 "Clicked or Not"으로 변환함
- cod-rna, ijcnn : Numerical Features만 포함함
- phishing : Categorical Features만 포함함
- adult : numerical과 Categorical Feature를 동시에 포함함

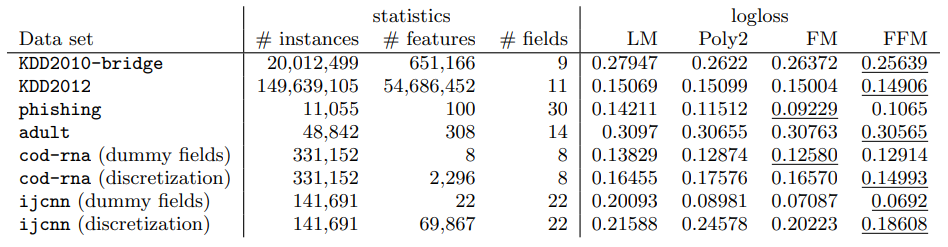
실험 Setting
- KDD2010-bridge, KDD2012, adult : 모든 Numerical Features를 29, 13, 94 bis로 Discretize
- cod-rna와 ijcn은 Dummy Field와 Discretization을 활용해 Section 3.3과 동일한 방식으로 진행
- Parameter Selection을 위해 4.5와 같은 절차를 거침

FFM은 KDD2010-bridge와 KDD2012에서 다른 모델보다 뛰어난 성능을 내었다.
Categorical Features를 Binary Features로 변환한 이후 결과가 Sparse하고 대부분 Features들이 Categorical하다는 특징을 가지고 있는 Dataset들이였다.

하지만 Phishing과 adult에서는 FFM이 좋은 성능을 보이지 못했다.
Phishing은 Data가 Sparse하지 않아 모든 모델에서 비슷한 성능을 냈고, adult에서는 모든 모델이 Linear Model과 비슷하게 동작하여 Conjunction이 유용하게 활용되지 않았다.

또한 Dataset이 오직 Numerical Features만 포함하고 있을 때 FFM은 큰 강점을 가지지 못했다.

Dummy Field를 활용할 경우 FFM은 FM보다 나쁜 성능을 냈고, Field Information을 나타내는 것은 결과에 도움을 주지 않았다.

우리는 FFM이 유용한 데이터셋들에 대한 가이드라인을 요약했다.

FFM은 Categorical Features를 포함하고, Binary Features로 전환된 Dataset에 대해 효율적
Sparse한 Data가 아니라면 이점을 지니지 못함
FFM을 Numerical Dataset에 적용하는 것은 어려움

Conclusion And Future Works

지금까지 FFMs의 효율성에 대해 논의함
- 특정 Dataset에서 FFMs는 학습 cost와 Logloss 측면에서 (원래 유명했던) Poly2, FMs, LM 모델보다 더 좋은 성능을 냄
Overfitting 문제에 조금 더 도전할 필요성이 존재함
쉬운 구현을 위해 SG를 활용했지만, 다른 Optimization Method(ex. Newton Method)는 FFMs에서 어떻게 동작하는지 관찰할 필요성이 존재함
- Gradient Method : f'(x) = 0이 되는 지점을 찾는 방법
  - 지점에서 Gradient를 구하고, Gradient의 반대 방향으로 x를 조금씩 이동시켜 극소점을 찾음
  - 모든 차원 및 공간에서 적용 가능하지만, Local Minima 문제에 빠질 수 있음
- Newton's Method : f(x) = 0의 해를 근사적으로 찾을 때 활용하는 방법
  - 점 x에서 접선을 긋고, 접선과 x축이 만나는 지점을 새로운 x로 지정하여 새로운 x에서 다시 접선을 그어 해를 찾아가는 방법
  - 초기값을 잘 주면 금방 해를 찾지만, 잘못 주면 시간이 더 오래 걸리거나 아예 해를 찾지 못할 수 있음
  - Gradient Method와는 달리 해에 근접할수록 수렴속도가 느려지는 문제점이 없음

DONGJIN IM

개념부터 확실히!

이전 포스트