Abstract

• CTR Prediction : Computational Advertising에서 중요한 역할을 수행

• 2개 모델이 이 Task에서 널리 활용됨

  • degree-2 Polynomial Mappings models : Poly2
  • Factorization Machines : FMs

• 논문에서 소개하는 모델 : Field-aware Factorization Machiens(FFMs)

  • FM의 변형
  • Large Sparse Data를 분류하는 가장 좋은 모델

• 논문에서 하고자 하는 것

  • FFMs 학습을 위해 실행한 효율적인 방법 설명
  • FFMs를 폭넓게 분석하여 다른 경쟁 모델과 비교

  ---

  Keywords

  Machine Learning

• 데이터를 통해 기계가 스스로 학습하게 하는 방법

  Click-through rate Prediction

• Click-through rate : 추천된 아이템을 유저가 클릭할 확률

• CTR Prediction

  • 추천 시스템에서 매우 중요한 요소 중 하나
  • 대부분의 추천 시스템에서 최대화하기 위해 노력하는 Task
  • CTR을 예측하기 위해 사용자의 Implicit Feature를 학습해야 함
  • Implicit Feature : User에 대한 정보
    • (ex) 성별, 나이대, 시간 등
    • (ex) 20대 남자는 6시 정도에 배달 앱을 많이 선택한다
      $\rightarrow$ Gender & 시간 2 Interaction으로 CTR Prediction을 수행

• Computational Advertising

  • 직역 : 컴퓨터 광고
  • 핵심 : 유저에게 맥락에 적합한 광고를 어떻게 제시할 것인가?
  • 즉, 컴퓨터를 통한 광고를 맥락에 맞게 하는 방법을 찾는 것이 Computational Advertising의 효과를 높이는 첫번째 방법인 것이며, 이를 위해 가장 많이 활용되는 Task가 CTR Prediction Task이다.

Factorization Machines(FMs)

• 사실상 이 논문보다 핵심인 것 같은 Model
• FFMs도 FMs의 변형이므로, 결국 FMs를 잘 알아야 FFMs도 잘 알 수 있음
• 따라서 원래 존재하지 않는 Section이지만 FMs에 대한 Section을 새로 만들겠다
  • 검색 등을 통해 이해한 내용을 바탕으로 정리한 것
  • 나중에 FMs에 대한 논문 정리를 하는 것을 추천함

---

Factorization Machines(FMs)

공부를 위해 많이 읽은 사이트

• https://supkoon.tistory.com/31
  • 정말 좋은 블로그 같아서 꼭 읽어보기를 추천

추천 시스템

추천 시스템을 배워본 적이 없으니 먼저 추천 시스템이 뭔지, 어떤 종류가 있는지부터 이해해야 이 논문을 이해할 수 있을 것이라고 생각한다.

추천 시스템은 위에서 말했듯 Computational Advertising의 효과를 높이는 분야라고 생각하면 편할 것 같다.
최근 너무 많은 빈도의 광고 때문에 사람들은 피로감을 크게 느낀다. 실제로 나도 페이스북 광고가 너무 많아지면서 페이스북의 사용 빈도가 떨어졌다.

하지만, 때론 적절한 광고는 도움이 되기도 한다.

예를 들어, 예전에 내가 다이어트를 하고 있을 때 닭가슴살 사이트가 광고가 나온적이 있었는데, 해당 앱을 다운 받고 거기에서만 닭가슴살을 주문하지 않는다.
즉, 이런 효율적인 광고를 더 많이 보여주기 위한 Task라고 보면 된다.

이런 문맥에 맞는 광고는 해당 사이트에 대한 신뢰감을 높이고, 광고사 또한 충성스러운 고객을 얻게 할 수 있는 장점을 가진다.

추천 시스템의 전략

Content-Based 전략

• User, Item에 대한 Profile을 생성하여 과거에 user가 접한 Item과 유사한 Item을 추천해주는 것

• 예시 : Netflix에서 User A가 본 영화에 대한 정보(장르, 배우, 별점 등)을 종합하여 이와 유사한 영화를 추천하는 전략

• 장점

  • 다른 유저에 대한 데이터가 필요하지 않음
  • 추천에 대한 근거를 어느 정도 증명할 수 있음

• 단점

  • Profile에서 필요한 Feature가 무엇인지 명확히 하는 과정이 어려움
  • Profile을 작성하지 못할 경우 새로운 User에 대한 추천이 어려움

Collaborative Filtering 전략

• Profile없이 과거 Interaction에 기반하여 추천을 제공해주는 것

• 예시 : 홈쇼핑에서 User A와 User B가 동일한 품목을 샀다. 이 때 User A가 C라는 물건을 샀고 User B가 C라는 물건을 사지 않았을 경우, User B 또한 C를 마음에 들어하지 않을까?

• 장점

  • Profile를 생성할 필요가 없음
  • 일반적으로 Content-based보다 좋음

• 단점

  • Interaction에 대한 데이터가 부족할 경우 추천 시스템이 제대로 동작하지 않음
  • 'Cold-start' : 서비스를 처음 참여한 유저는 유저에 대한 데이터가 부족하므로 추천 시스템이 제대로 작동하지 않음
    • 이 문제를 해결하기 위해 처음에 user에 대한 질문을 하는 경우도 있고, 그냥 처음에는 막 추천하다가 점차 성능을 높이는 경우도 존재함

• Neighborhood method

  • Item 혹은 User 사이 관계를 계산하는데 초점을 맞추는 방식
  • item-oriented : 동일한 유저에게 비슷한 평가를 받아 item을 이웃하다고 설정하는 것
    user-oriented : 동일한 아이템에게 비슷한 평가를 내린 유저를 이웃하다고 설정하는 것

• Latent Factor Model

  • 이번 논문을 이해하기 위해 잘 알아야 하는 개념
  • User가 Item을 평가하는 과정에서 추출된 Latent Factor를 이용하여 user와 item을 함께 특성화 하는 방법
    • (ex) Factor : Gender, 나이, 성별 등

Latent Vector라는 말이 논문에 많이 나와 이 말의 의미가 신경 쓰였는데, 그냥 "특징"이라고만 생각하면 된다.
Latent가 앞에 붙은 것은, 결국 이 특징들은 서비스 겉으로 드러나지 않는, Model의 Input으로만 주어지는 특징들이기 때문에 앞에 "잠재"라는 뜻인 Latent를 붙인 것 같다.
즉, User는 해당 Data를 활용해 추천 시스템이 동작하는지 모르지만, 실제로는 활용하는 Vector라는 것이다

Matrix Factorization

User와 Item 간의 평가 정보를 나타내는 Rating Matrix를 User Latent Matrix와 Item Latent Matrix로 분해하는 기법이다.

이를 풀어 말해보자.
먼저, User가 Item에 대해 직접적으로 평가한 자료가 있을 것이다. 이를 2차원 Matrix로 만든다.
이후 이 Matrix를 User Latent Vector와 Item Latent Vector로 쪼개는 것이다.

문제는 Rating Matrix는 (대부분) Sparse Matrix가 된다는 것이다.
실제로 특정 물건을 사거나 선호도가 있더라도, 평점을 달지 않는 경우도 많기 때문이다.

Matrix Factorization은 위와 같은 행렬 분해 과정에서 Spare Matrix의 빈칸을 채울만한 평점을 예측하는 과정이라고 생각하면 된다.

기존 시스템은 이런 결측치를 채우는 과정에 신경썼지만, Sparse한 데이터의 차원이 커질수록 계산 부담이 커지고 데이터가 왜곡될 가능성이 높아졌다.

따라서, 최근에는 존재하는 데이터만을 이용하는 방법을 많이 활용한다.

맨처음 User Latent Matrix와 Item Latent Matrix을 임의의 값으로 채워넣는다.
이후 User와 Item Latent Matrix의 Weight값을 변경하여 최소한 기존 Rating Matrix와 유사하도록 학습이 진행되는 것이다.
이를 Gradient Descent라고 한다.

아 이제 내가 공부한 내용이 나왔다. GD!
즉, 이제 나는 Gradient Descent 기법을 활용하여 User Latenet Matrix와 Item Latent Matrix곱을 통해 얻어진 Matrix를 Prediction, 기존 Rating Matrix를 Label값으로 생각하여 둘 사이의 오차값이 최소화하는 방향으로 학습이 진행되면 되는 것이다.

• Reguarized Squared Error 수식
  $min_{q,p}\sum_{(u,i)\in K}(r_{ui} - p_uq_i^T)^2 + \lambda(||q_i||^2 + ||p_u||^2)$
  • $r$ : Rating Matrix
  • $p$ : User Matrix
  • $q$ : Item Matrix
  • $\lambda$ : Overfitting 방지용 Regularization

K에 대한 설명

Rating Matrix의 Size는 (User 수 X Item 수)이다.

이를 2개의 Matrix로 쪼개는데, 이 때 2개의 Matrix Size도 결정되어 있어야 한다.

이 때 User Matrix의 Size는 (User 수 X K), Item Matrix의 Size는 (Item 수 X K)로 지정한다.
이 때 K는 user가 지정해주는 Parameter이다.

그리고, 위 식에서 활용하는 K 또한 Matrix Size를 위해 user가 지정한 Parameter값이다.

MF에서 Gradient Descent를 활용한 학습 기법

SGD

논문에서는 SG라고 말한 기법이다.

이전에 공부했던 대로, 단순히 Gradient를 계산한 이후 Gloabl Minmize를 찾을 수 있는 방향으로 학습이 진행되는 것이다.

구현이 쉽고 빠르다는 장점이 있다.

ALS(Alternating Least Squres)

User와 Item의 Latent Vector는 모두 미지의 값이므로, Regularized Squared Error가 Convex하다는 보장이 없다.

즉, Global Minmum이 존재한다는 보장이 없는 것이다.

하지만, 두개 벡터 중 한 개를 곶어시키면 Convex한 2차식이 되어 최적화가 가능해진다.

따라서, $q_i$와 $p_u$를 번갈아가며 고정시키면서 최적화를 하는 방식이다.
ALS는 Implicit Data에 집중된 Data이거나 병렬화가 가능할 경우 효과적인 학습 방법이다.

FMs

Matrix Factorization의 단점

• 일반적인 데이터에 바로 적용할 수가 없음

• 대부분의 경우 Task Specific한 모델

• 이러한 단점을 해결하기 위해 SVM과 MF의 장점을 동시에 가지고 있는 FMs Model이 발표됨

  • SVM의 장점 : 데이터 형태에 규제받지 않고 분류, 회귀 등 다양한 작업을 수행할 수 있음

FMs의 장점

• Sparse Data에도 활용 가능

  • SVM에서는 Sparse Data일 경우에 Parameter 추정이 어려웠음
  • FMs에서는 Sparse Data에서도 학습이 가능함

• Linear Complexity

• General Predictor

  • 실수 벡터를 활용하더라도 잘 작동함

FMs 동작 과정

FMs Input

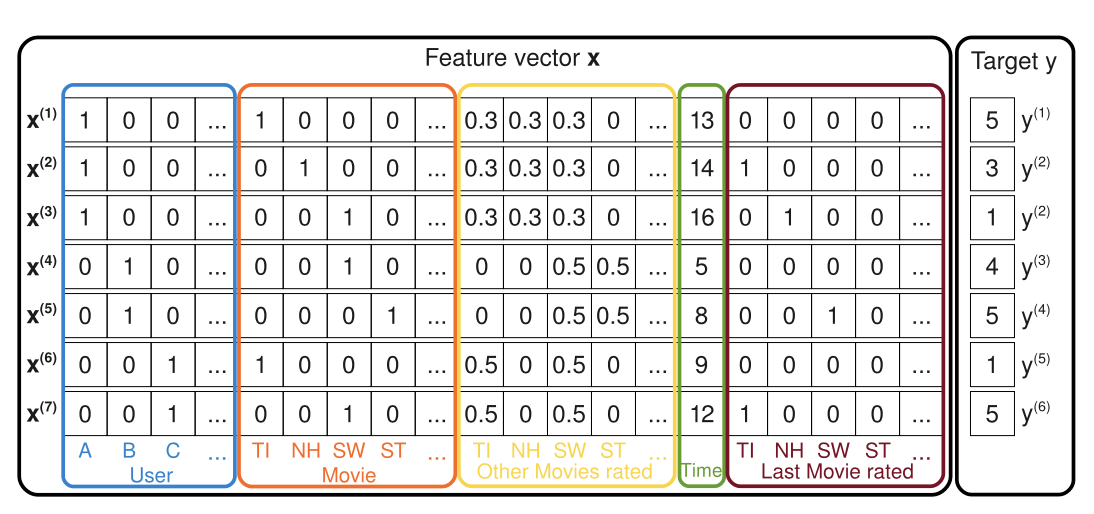
• 출처 : Factorization Machines(paper)
• $v_i$ : 각 Feature의 잠재벡터

MF에서는 User, Item, Rating만을 활용했지만 FM은 다양한 Feature를 Concat하여 1개의 Feature Vector를 만들고, 이를 Input으로 넣어준다.
즉, Explicit 뿐만이 아닌 Implicit한 특성이라도 실수 형태로 x Vector에 추가시킬 수 있다.

FMs에서는 User, Item과 같은 Categorical Feature를 One-hot 형태로 표현하여 x에 추가하기 때문에 일반적으로 Input Data x는 Sparse한 Vector가 된다.

이처럼 Feature Vector를 형성한 뒤, 바로 가중치 행렬 W에 x를 곱하여 W를 구하는 방식으로 학습하지 않는다.
대신 V라는 Matrix를 활용하여 W를 분해한 뒤 (Factorize) V를 학습하는 방향으로 진행된다.
(여기는 MF와 비슷한 형식)

일반족으로 Positive definite matrix W에 대해서는 충분히 큰 k에 대해 $W = V \dot V^T$를 만족하는 V가 존재한다고 알려져있고, 이는 W를 V안에 포함된 잠재벡터 $v_i$의 내적으로 표현할 수 있다는 의미이다.
(Sparse Data를 많이 활용하므로 좋은 일반화를 위해 k를 어느정도 작게 잡는다)

즉, f개 Latent Vector로 표현된 $v_i$ 간의 2-way Interaction의 내적값과 $v_i$와 대응하는 $x_i$ 곱을 활용하여 최적화를 진행하는 것이다.

FM의 가장 큰 특징은 특성마다 Latent Space로의 Mapping을 진행하고, Latent Space에서의 내적을 계산한다는 것이다. 이를 Factorized Parametrization이라고 한다.

이를 수식으로 나타내면 아래와 같다