Numpy란?

numpy는 C언어로 구현된 Python Library로써 고성능 과학 계산을 위해 만들어졌다.

Numerical Python의 줄임말로써, Python Array 연산의 표준이 되는 ndarray를 기본으로 활용하고 있다.

Numpy의 장점은?

1. 일반 Python List보다 빠르고 메모리 효율이 좋아 많이 활용된다.

Python List는 리스트 공간 하나에 메모리를 한 개씩 공유하게 된다. 즉, arr[1]과 arr[2]의 주솟값에는 서로 연관성이 없는 것이다.
하지만, ndarray는 리스트 하나를 메모리 하나에 넣어주기 때문에 훨씬 빠르고 메모리 효율이 좋아지는 것이다. 즉, 공간 Locality를 가지게 되는 것이다.
왜냐하면 arr[2]를 접근하려면 arr[1]에서 원소 크기만큼의 주솟값만 더해주면 바로 arr[2]로 갈 수 있기 때문이다.
이런 차이가 나타나는 이유는 Python List는 여러 type 원소들이 한번에 저장될 수 있지만, ndarray는 1개 type 원소로만 구성될 수 있기 때문일 것이다. 즉, Python List는 arr[1]에서 String만큼 공간을 할당해야할지, int만큼 할당해야할지 모르기 때문에 Memory를 따로 할당하지만, ndarray는 C언어와 마찬가지로 1개 Type으로만 구성되어 있으므로 메모리를 한꺼번에 할당해도 별 문제가 존재하지 않는다.
JAVA나 C언어도 공부했던 사람으로써 과연 여러 type 원소들을 한번에 저장할 수 있는 것에 대한 메리트가 있을지 의문이였는데, ndarray를 따로 생성한 것을 보니 메리트보다는 디메리트가 더 큰 것이 아닐까 싶다.

2. 반복문 없는 배열 처리를 지원한다.

예시로 보는 것이 가장 빠르다

# Case1 : Python List끼리의 합
arr1 = [1,2,3]
arr2 = [3,4,5]
arr1 + arr2 # 답 : [1,2,3,3,4,5]


# Case2 : ndarray끼리의 합
nd_arr1 = np.array(arr1, int)
nd_arr2 = np.array(arr2, int)
nd_arr1 + nd_arr2 # 답 : array([4,6,8])

위 예시를 보자. Case1에서는 arr1 + arr2를 수행하였을 때 List끼리 Concat되는 것을 알 수 있다. 하지만, 덧셈 연산을 할 때 Concat이 아닌 "같은 위치의 원소끼리의 합"을 구하고 싶은 경우가 더 많다.
Case2를 보면, (4,6,8) = (1+3, 2+4, 3+5)로 연산이 수행됨을 알 수 있다. 즉, "같은 위치에 존재하는 원소끼리의 합"연산이 수행되었음을 알 수 있다.
이런 연산은 과학적인 연산을 수행할 때 큰 도움이 된다.

3. 선형 대수와 관련된 다양한 기능 제공

알다시피 AI 기술에는 선형 대수 관련 수학 공식들이 많이 들어간다. 그리고, Numpy는 이를 위한 기능을 제공해주기에 매우 큰 도움이 된다.
예를 들어 Matrix Determinant를 구하다고 가정해보자. 원래라면 Python에서는 수학과에서 배운 연산을 활용하여 함수 하나를 정의해야 할 것이다.
하지만, Numpy는 np.linalg.det({ndarray})메서드를 활용하면 ndarray에서 바로 Determinant를 구할 수 있다.

---

Numpy 중요 개념

ndim

Numpy 배열의 차원 수 혹은 축의 수를 말하는 용어이다.
즉, Numpy 배열이 몇 차원 배열인지를 의미하는 단어이다.
(ex) np.array([[1,2,3],[4,5,6]]) : 2차원 Matrix이므로 ndim = 2이다.

Shape

Numpy 배열 차원 크기를 Tuple 형태로 표현한다.
n행과 m일 경우 (n,m)으로 표시하며, 만약 1행만 존재할 경우 (m,)를 출력한다.
(ex) np.array([1,2,3,4,5]) : (5,)로 출력한다(즉, 1은 생략한다)
(ex) np.array([[1,2,3],[4,5,6]]) : (2,3)으로 출력한다.

dtype

Numpy Matrix의 Element Data Type을 의미한다.

Axis

Numpy 뿐만이 아니라 AI에서는 매우 중요한 개념이다. 나중에 dim이라는 Parameter로 전달할 때도 있지만, 결국 dim도 axis와 같은 개념을 공유하고 있고, 실제로 두 Parameter 모두 활용할 수 있는 메서드들도 많다.

먼저 개념적으로 따지면, Operation 때 기준이 되는 축이 Axis라고 말하면 될 것이다.
(A, B, C)가 존재할 때, axis = 0은 A, axis = 1은 B, axis = 2일 때는 C에 존재하는 원소들을 연산 기준으로 삼은 것이다.

그런데 나는 이 말을 도대체가 이해할 수 없어서, 직접 axis에 대한 여러 실험을 해보며 내 방식대로 이해했다.

나는 Axis를 따라 Operation을 수행할 원소를 뽑는 거름망이 움직인다고 생각하였다.

예를 들어, axis = 0으로 설정한 이후 합 연산이 수행된다고 생각하자.
그렇다면, 합을 시킬 원소들은 axis = 0 방향으로 거름망이 움직이며 원소를 선택한다고 생각하였다. 즉, 다른 axis에 해당하는 거름망은 다 막혀있고 오직 axis=0인 부분의 거름망만 뚤려있는 것이다.
거름망은 A = 0인 구간에서 답을 하나 고르고, A = 1인 구간에서 답을 하나 고르는 방식으로 움직이는 방향으로 1개씩 답을 고르는 것이다.
이에 따라, axis = 0인 경우 우리가 고르는 원소는 arr[0,B,C], arr[1,B,C],..., arr[N,B,C]이 될 것이며, 이 모든 원소의 합을 구하는 것이 axis = 0일 때의 result[B,C]의 값을 구하는 방법이 될 것이다.

Broadcasting

Numpy에서 Shape가 다른 배열 간 연산을 지원하는 기능이다.

아래 그림은 Broadcasting을 가장 잘 설명한 그림이다.

• 출처 : http://www.astroml.org/book_figures/appendix/fig_broadcast_visual.html

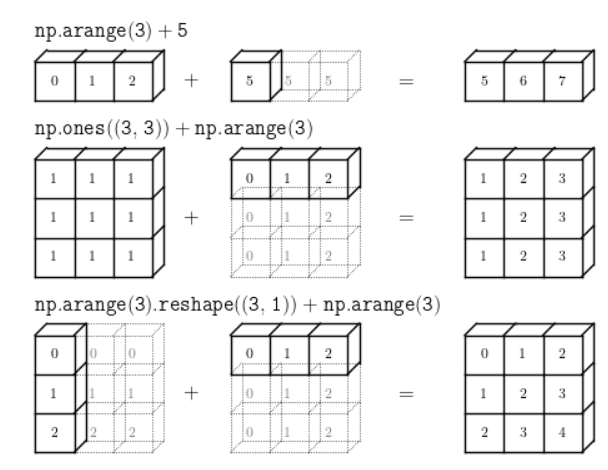
그림에서 보다시피, 작은 Matrix나 Scalar를 복제하여 큰 Matrix 형태로 만든 뒤, 연산을 수행하는 방식을 채택하고 있다.

위 사진에서는 사칙연산에 대한 Broadcasting을 표현했지만, ">", "<" 같은 비교 연산을 수행할 때도 Broadcasting을 활용할 수 있다.

Matrix와 Sclar 사이에는 무조건 Broadcasting 연산을 수행할 수 있으며, Matrix와 Matrix 사이 Broadcasting이 수행되기 위해서는 몇 가지 조건이 필요하다.
이는 Scalar는 자신의 값을 복제하여 어떤 형태의 Matrix도 형성할 수 있지만, Matrix와 Matrix 사이에 Broadcasting이 수행되기 위해서는 Matrix값이 그대로 복사되어야 하고 손실이 없어야 하기 때문에, 특정 Matrix Shape를 만들 수 없기 때문이다.
(ex) "4"라는 Scalar 값을 복사하면 (A,B)에서 A, B 값과 관계 없이 Matrix를 형성할 수 있다.
하지만, [1,2]라는 Matrix가 존재할 경우, (1,2) 형태를 지님을 알 수 있다. 이 때, (3,3) Matrix 연산과 수행한다고 가정하자.
이 때 [[1,2],[1,2],[1,2]]로 (3,2) Matrix까지는 만들 수 있을 것이다. 하지만, (3,3)은 손실 없이는 만들 수 없는 Matrix Shape가 될 것이다. 따라서, 몇 가지 조건이 필요한 것이다.

조건은 아래와 같다.
1. 두 배열이 뒤에서부터 대응하는 축의 크기가 동일해야 함
2. 대응하는 축 중 어느 한 쪽의 축 크기가 1이여야 함

(ex1) Shape가 (3,7,5)인 Matrix가 존재하고, (7,5)인 Matrix가 존재한다고 가정하자.
이 경우, 뒤에서부터 축의 크기를 비교하면 5, 7로 동일하기 때문에 Broadcasting이 수행될 수 있는 Matrix 쌍이다.
결과 Matrix는 (3,7,5) Shape를 가질 것이다.
(ex2) Shape가 (4,1,5)인 Matrix와 (3,5)인 Matrix가 존재한다고 가정하자. 이 경우, 1과 3으로 축의 크기가 다르긴 하지만, 조건 중 2번을 만족시키므로 Broadcasting이 수행될 수 있다.
결과 Matrix는 (4,3,5) Shape를 가질 것이다.
(ex3) Shape가 (3,2,5)인 Matrix와 (3,5)인 Matrix는 1,2 조건 모두 만족시키지 않으므로 Broadcasting 연산이 불가하다.
(ex4) (1,3)과 (3,1) Matrix가 존재할 때,축의 크기가 모두 다르지만 한 쪽이 1의 크기를 가지기 때문에 Broadcasting이 수행될 수 있다.
결과 Matrix는 (3,3) Shape를 가질 것이다.

---

Numpy 사용법

• numpy의 모든 API : https://numpy.org/doc/stable/reference/index.html

numpy 호출

• 일반적으로 np라는 alias를 이용하여 호출

import numpy as np

ndarray

• Numpy를 통해 만들어진 Array
• 1개의 데이터 Type으로만 이루어질 수 있음
• 생성 방법 : np.array({Python List}, dtype})

ndarray = np.array(["1", 3.5, 1], float)
# "1", 3.5, 1 모두 float형으로 변환되어 ndarray를 생성

ndarray의 dtype 및 Shape 알아내기

# dtype 알아내기
ndarray.dtype

# shape 알아내기
ndarray.shape

ndarray의 원소 접근

• 행과 열을 각각 Slicing하여 접근 가능
  • ndarray[:3, 2:4]로 Slicing 가능
• Index를 1개 List에 담아 접근 가능
  • Python List는 a[0][0] 방법으로만 접근 가능하지만, ndarray에서는 a[0,0]으로 접근 가능

Numpy 비교 연산(모든 원소에 대해)

• all : "모든" 원소가 비교 연산에서 True를 반환해야지만 True
• any : 한 개의 원소라도 비교 연산에서 True를 반환한다면 True

np.all(matrix>5) # matrix 모든 원소가 5보다 커야 True
np.any(matrix>5) # matrix 원소 중 하나라도 5보다 크면 True

유용한 행렬 만들기

np.ones(shape=(a,b)) # shape에 따라 Matrix를 생성 후 1로 값 초기화
np.zeros(shape=(a,b)) # shape에 따라 Matrix를 생성 후 0으로 값 초기화

np.ones_like(matrix) # matrix의 Shape와 동일한 Shape로 Matrix 생성
# ones_like : 1로 값 초기화, zeros_like : 0으로 값 초기화

np.identity(k) # k*k 단위 행렬 생성

np.eye(N,M,k)
# Default k = 0
# N*M 행렬에서 arr[0,k] 부터 대각선(오른쪽 아래) 모든 공간을 1로 채움

np.diag(matrix,k) 
# matrix[0,k]부터 대각선(오른쪽 아래) 모든 원소를 ndarray 형태로 반환

ndarray 2개 통합

np.vstack((a,b)) # a matrix "아래로" b matrix 합침
np.hstack((a,b)) # a matrix "오른쪽으로" b matrix 합침

np.concatenate((a,b), axis = 1)
# axis = 1 방향으로 a matrix에 b matrix를 붙임
# 거름망은 왼쪽 -> 오른쪽으로 이동하므로, 오른쪽에 b matrix 붙임

최대, 최솟값 확인

• 매우 많이 활용되기 때문에 꼭 잘 알아두기
• argmax : 최댓값이 존재하는 Index 반환
• max : 최대값 반환
  • 나중에 배울 torch.max는 Index와 최댓값을 동시에 반환함

np.argmax(matrix) # matrix 최댓값 "index" 반환
np.argmin(matrix) # matrix 최솟값 "index" 반환

np.argmax(matrix, axis = 1) 
# axis = 1방향으로 최댓값 index 반환
# 거름망은 왼쪽 -> 오른쪽으로 이동하므로, Row마다의 최댓값 index를 반환

arrange

• a 이상 b 미만 수를 c만큼 증가시켜 ndarray 원소로 담아 반환
  • Default c : 1, Default a : 0
  • a를 생략하고 싶을 경우, c는 무조건 생략되어 있어야 함

np.arrange(a, b, c)

ndarray간 연산

• 사칙 연산을 지원함
  • 이 때, 사칙 연산은 Element-wise operations
  • Element-wise operations : 같은 위치에 존재하는 원소끼리 연산 수행
• Dot Product

matrix_a.dot(matrix_b)

행렬 Transpose($A^T$)

matrix.transpose()
matrix.T

Numpy 비교 연산(각 원소에 대해)

• Broadcasting을 통해 연산 수행
• 1개 비교 연산 수행

a = np.arrange(5)
a > 2
# 결과 : [False, False, False, True, True]

• 2개 비교 연산 동시 수행
  • logical_and : 2개 비교 연산을 모두 만족하는지 확인하여 Boolean형 ndarray 반환
  • logical_or : 2개 비교 연산 중 하나 이상을 만족하는지 확인하여 Boolean형 ndarray반환

np.logical_and(a > 0, a<3)

np.logical_or(a > 0, a < -1)

np.where

• np.where({조건문}, A, B) : True인 index에는 A를, False인 index에는 B를 넣어 Array 형성
• np.where({조건문}) : True인 index를 ndarray 형태로 반환

Boolean Index

• Shape가 같은 2 Matrix 사이에서 수행되어야 함
  • 1개 Matrix는 무조건 Boolean형 ndarray
• Boolean형 Index 중 True인 곳에 존재하는 Data만 추출

A = [True, True, False]
test_array[A]

"""
Shape이 같다면, A 중 True 값을 가진 index에 저장된 "test_array값"만 반환 됨
test_array = [1,2,3]일 경우, 답은 [1,2]가 될 것이다.
"""

Fancy Index

• int형 Array를 통해 Matrix 원소 접근 가능
• Shape가 같지 않아도 됨
  • 단, Dimension이 다를 경우, 차이 나는 Dimension 만큼의 Vector가 준비되어야 함

A = np.array([2,4,6], int)
B = np.array([0,1,2,1,0], int)

A[B]

"""
우리가 출력하고 싶은 것은 "A의 원소"이다.
따라서, A[B[0]], A[B[1]], A[B[2]] 순으로 접근하는 것이다.
즉, A[B] = [A[0],A[1],A[2],A[1],A[0]] = [2,4,6,4,2]가 될 것이다.
"""

Numpy I/O

• Numpy I/O보다는 Pickle이나 DataFrame으로 변환한 뒤 Pickle을 활용하는 경우가 많은 것 같은데, 일단 알아는 두자.
• np.loadtxt("파일 경로") : 경로에 존재하는 파일 Data 불러옴
• np.savetxt("파일 경로", Data, delimiter=",") # Data를 파일 경로에 저장
• np.load(), np.save()로도 수행 가능

---

Reshape와 Resize

개념적 설명

Reshape와 Resize는 매우 중요한 내용이기 때문에 아예 따로 Section을 만들었다.

Reshape와 Resize는 Ndarray의 Shape를 변경하는 API라는 공통점을 가지고 있다.

하지만 두 API 사이에는 큰 차이점이 존재한다.

1. API를 통해 만들어진 배열과 원본 배열의 관계
Reshape는 얕은 복사와 비슷하게 연산이 수행된다.
원본 Array 값이 변경된다면 Reshape를 통해 만들어진 배열 값도 동시에 변경된다.
하지만 Resize는 깊은 복사처럼 연산이 수행된다.
즉, Resize를 통해 배열을 만들었다면 원본 배열과는 아예 무관한 배열이 되는 것이다.

2. 연산에 필요한 원소 개수
Reshape는 원본 배열 원소 개수와 Reshape 이후 배열 원소 개수는 무조건 동일해야 한다.
즉, 원본 Matrix가 (A, B) Shape를 가졌다면, Reshape 이후 배열은 형태가 어떻게 되었든 Shape 축의 값을 모두 곱했을 때 A * B값을 가지고 있어야 하는 것이다.
하지만 Resize는 굳이 동일할 필요는 없다.

Resize 시킨 배열 원소 개수와 원본 배열 개수가 다르다면 어떻게 될까?

Resize 또한 원본 배열을 변형시키는 것인데, 개수가 다르다면 부족한 값은 어떻게 가져올지 궁금할 수 있다.
아래 코드를 통해 확인하자.

X = np.array([[10,20,30],[40,50,60]])
np.resize(X, (1,8))

• 답 : array([[10, 20, 30, 40, 50, 60, 10, 20]])

X의 원소 개수는 6이지만, resize 이후 원소 개수는 8개이다. 즉, 2개원소가 더 필요한 것이다.
추가로 필요한 2개 원소는 X[0,0]부터 X[0,1]까지 총 2개 원소를 복사하여 Resize시킨다

Reshape와 Resize의 활용법

# Reshape
ndarray.reshape(x,y,...) # ndarray를 (x,y,...) 꼴의 Shape로 변경

# Resize
ndarray.resize(x,y,...) # ndarray를 (x,y,...) 꼴의 Shape로 변경

-1의 활용

이 때 Reshape의 가장 큰 특징은 "-1"을 Parameter로 전달 할 수 있다는 점에 있을 것이다. np.array(matrix).reshape(-1,4)와 같이 설정할 경우, Matrix의 원소 개수에 맞춰 자동으로 축 크기를 설정해 줄 것이다.
예를 들어, Matrix가 8개 원소를 가지고 있다면 -1 대신 2라는 값이 들어가 Reshape 메서드가 수행될 것이다
하지만 Resize에는 -1을 절대로 넣을 수 없다. 왜 이런 차이가 생길까?

Reshape의 -1에 대한 개인적 이해

위에서 말했듯, reshape 시킨 배열 원소 개수와 원본 배열 원소 개수는 무조건 같다. 이를 조금 더 생각해보자면, 만약 1개 dimension을 제외하고 모든 dimension이 정해졌다면, 마지막 dimension은 자동으로 결정된다는 의미이다.

예를 들어, matrix가 총 8개 원소를 가지고 있고, axis = 1 방향으로 4의 dimension을 가진다고 가정하자. 그렇다면, axis = 0 방향으로는 2의 dimension을 가져야만 원소 개수가 일치할 것이다.
즉, 이렇게 (다른 원소에 의해) 자동으로 결정되는 dimension 공간에 -1을 입력하면 해당 dimension을 python에서 자동으로 계산해준 이후 Reshape 시킨다.

Resize는 원본 배열 원소 개수와 Resize 시킨 배열 원소 개수가 같지 않아도 되기 때문에 -1을 활용하지는 못한다.

---

• 사진출처
  http://www.astroml.org/book_figures/appendix/fig_broadcast_visual.html