PyTorch와 TensorFlow

• PyTorch와 TensorFlow를 잘 비교해 놓은 사이트 : https://data-newbie.tistory.com/425

TensorFlow

장점

1. 압도적으로 쉬운 배포(Production)
PyTorch와는 다르게 TensorFlow로 만든 모델은 REST Client API를 활용한 Tensorflow Serving이 가능하여 바로 모델 배포가 가능하다.
또한 Tensorflow 자체가 산업에서 요구하는 요구사항을 중심으로 만들어진 것이기 때문에 산업 요구사항을 잘 만족시킨다는 장점이 있다.

2. Scalability
Scalability(범위성)은 제품이 사융자의 요구에 맞추기 위해 크기나 용량을 변경해도 기능이 변경 없이 잘 동작할 수 있는 능력을 의미한다.

3. Mobile 지원

4. 로그를 그래프로 편리하게 확인할 수 있는 툴 제공

구현 패러다임 : Define-and-Run

간단히 말하자면 Static Graph를 활용한다고 말할 수 있다.
먼저 모델을 형성한 뒤, 데이터를 입력시켜 학습을 진행시키는 방식으로 진행이 된다.
값을 담을 공간(Function)을 미리 정의하고, 함수가 돌아갈 때 값을 넣어주는 방식을 활용한다.

PyTorch

장점

1. Simplicity
Numpy와 매우 유사한 특성을 가진다. 또한 Pythonic하게 코드를 짤 수 있어 입문자에게는 매우 쉽다는 특성을 가진다.

2. Great API
TensorFlow는 변경이 너무 잦아 Update 때마다 힘들어질 수 있다. 하지만 Pytorch는 변경이 잦지 않으므로 대부분의 API는 PyTorch를 지원하도록 만든다

3. Multi-GPU 지원

구현 패러다임 : Define-by-Run

Dynamic Computation Graph를 활용하는 방식이라고 할 수 있다.
실행하면서 그래프를 생성하는 방식으로, 중간 중간 그래프 확인이 가능하다는 특징이 있다.
중간 값 확인이 가능하기 때문에 Debug가 쉽다는 장점이 있다.

Define-by-run VS Define-and-run

• 그림으로 보는 차이 : https://medium.com/@zzemb6/define-and-run-vs-define-by-run-b527d127e13a

Define-by-run은 함수를 만들고 Data를 Feeding만 하면 결과를 도출하는 방식을 활용하고 있다. 즉, 함수를 돌리는 코더는 중간 과정을 몰라도 된다는 것이다
(어차피 함수를 한 번 만들어지기만 하면 알아서 돌릴 것이다)

Define-and-run은 함수를 만듦과 동시에 Data를 같이 먹여주어 특정 Layer 값을 Output으로 뽑을 수도 있다.
즉, 중간 과정도 코더가 알 수 있고, 따라서 어떤 부분에서 에러가 발생하는지 등의 Debug가 쉬워진다는 장점이 있다.
데이터를 첫번째 Layer에 먹여주고, 마지막 Layer까지 형성되는 방식을 학습이 진행될 때마다 수행된다고 생각하면 될 것 같다.

이를 잘 비유한 것은 "리모컨"과 "기판"인 것 같다.
Tensorflow는 리모컨이고, Pytorch는 기판의 역할이다.

Tensorflow는 리모컨을 클릭하면 미리 정해져 있는 함수(ex. 전원 버튼을 누르면 TV가 켜진다)가 수행되는 형식이다.
따라서 리모컨의 사용법을 알아야 하지만, 한 번 알고 나면 편하게 쓸 수 있다. 또한 어떤 형식으로 그 로직이 수행되는지는 몰라도 되지만, 대신 고장이 났을 경우 어떤 중간 과정에서 고장이 난지는 잘 모를 것이다.

PyTorch는 기판이다. 기판을 통해 전원을 키려면 해당 기판이 어떤 역할을 수행하고, 어떤 Output 신호를 보내는지 정확히 알아야 한다.
따라서 코드를 실행하기에는 Tensorflow보다 어려울 수 있다. 하지만, 기판의 종류를 내가 이었기 때문에 어떤 기판이 어떤 역할을 하는지 잘 알 수 있으며, 신호를 반환하는 기기를 달면 중간 출력 결과도 알 수 있을 것이다. 또한, 중간 과정을 모두 볼 수 있으므로 고장이 났을 때 어떤 부분에서 고장이 났는지 쉽게 알 수 있다.

---

PyTorch

PyTorch란?

Torch를 기반으로 하는 오픈 소스 머신 러닝 라이브러리이다.
참고로 Torch는 Facebook에서 제공하는 딥러닝 도구로써 Numpy와 효율적인 연동을 지원하는 편리한 도구이다.

PyTorch의 기본 Data Structure는 Tensor이다.
Tensor는 Numpy 배열과 매우 유사한데 CUDA를 지원하는 GPU에서도 사용할 수 있다는 특징을 가지고 있다.
그래서 코드를 짜다보면 가끔 Numpy는 CUDA로 옮길 수 없다는 경고문이 뜰 때가 있는데, Tensor가 CUDA를 지원하는 것이기 때문에 Tensor객체로 형태를 변형시켜줘야 한다.

PyTorch에서 지원하는 모듈은 매우 다양하다.
먼저 자동 미분 모듈(Autograd)가 존재한다.
간단히 "Backpropagation"을 자동으로 수행해주는 모듈이다 라는 정도만 알고 있어도 충분할 것이다.

또한 최적화 모듈이 존재한다.
이는 torch.optim으로 호출할 수 있는데, optimizer나 Loss Function 등 최적화를 위해 필요한 도구들이 저장되어 있다.
Loss Function이나 Optimizer는 nn 모듈로 구현하는 경우도 있지만, 많은 Case에서 최적화 모듈에 존재하고 있는 함수를 활용한다
(매우 많은 도구들이 저장되어 있으니, 먼저 존재 여부를 확인 후 없을 때만 구현하도록 하자)

마지막으로 nn 모듈이 존재한다.
Autograd 모듈은 Backpropagation을 쉽게 해주지만, Network를 구현할 때는 너무 고수준의 모듈이 된다.
따라서, Network를 정의하는 낮은 수준의 작업을 위해서 구현된 모듈이다.

즉 PyTorch는 Tensor(Numpy) + Autograd(자동 미분) + Function(Module)로 구성되어 있다고 말할 수 있다.

Tensor

GPU에 Tensor 객체 저장

• 1번 방법 : Tensor 객체를 생성할 때 바로 지정

torch.cuda.FloatTensor({Python List})

• 2번 방법 : Device 객체를 선언 후, 해당 객체 설정을 Tensor에 입혀줌
  • 자주 활용하는 방법
  • torch.cuda.is_available()을 통해 GPU 연결 여부를 확인 할 수도 있음

device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
# GPU와 연결되어 있으면 cuda:0 GPU와 연결시키고, 아닐 경우 CPU와 연결시켜라
  
y = x.to(device)

Tensor 객체 생성 방법

import torch

# 방법 1
torch.tensor({Python_List or ndarray})

# 방법 2
torch.from_numpy(ndarray)
# torch.to_numpy({Tensor 객체})로 tensor객체를 ndarray로 변경 가능

# 방법 3
torch.FloatTensor({Python_List or ndarray})
# torch.tensor로 Torch 객체를 생성할 경우 자동으로 FloatTensor로 생성됨

Tensor operation

Numpy와 매우 유사하다.

단지, 행렬 곱을 수행할 때 Numpy는 .dot을 활용하지만 PyTorch에서는 torch.mm 혹은 torch.matmul을 활용한다.

Tensor 객체 Dimension 조정

• view : 내가 원하는 Dimension 형식으로 변경
  • Numpy의 Reshape와 동일한 메서드
  • PyTorch에서도 Reshape() 메서드가 존재하며 Reshape()와 수행 결과는 비슷해보이지만, 엄연한 차이가 존재한다. 이는 아래에서 Contiguous를 설명하며 자세히 설명하겠다.
• squeeze : 차원 size가 1인 Dimension 삭제
• unsqueeze(n) : Axis = n인 공간에 차원 Size가 1인 Dimension 생성

torch.nn.functional 모듈

torch.nn.functional 모듈이란?

위에서 말했듯, torch.nn은 Autograd보다 저레벨에서 구현되어야 하는 객체를 위한 모듈이다.
torch.nn.functional은 이 중 다양한 수식 변환을 지원하는 모듈이다.

대표적 함수

• softmax({Tensor 객체}) : softmax 함수 수행
• one_hot({Tensor 객체}) : one-hot 함수 수행

언더바(_)

• 언더바가 없는 메서드의 경우 메서드를 수행한 뒤의 결과를 "새로운 객체"로 반환함.
  • 원래 객체는 변경되지 않음
• 언더바가 있는 메서드의 경우 메서드를 수행한 뒤의 결과를 해당 메서드를 수행시킨 객체(기존 tensor)에 적용시킴
  • 원래 객체 값이 변경됨
• 코드를 통하 ㄴ이해

B = torch.FloatTensor([[1,2,3],[4,5,6]])

print(B.mul(2.))
print(B)
print(B.mul_(2.))
print(B)
  
""" 
결과
  
tensor([[ 2.,  4.,  6.],
        [ 8., 10., 12.]])
tensor([[1., 2., 3.],
        [4., 5., 6.]])
tensor([[ 2.,  4.,  6.],
        [ 8., 10., 12.]])
tensor([[ 2.,  4.,  6.],
        [ 8., 10., 12.]])
"""

• 위 예시를 보면, B.mul(2.)을 수행했을 때는 B값이 바뀌지 않지만, B.mul_(2.)을 수행하면 (언더바가 있는 메서드이므로) inplace=True로 고려되어 B값 자체가 변화하는 것을 볼 수 있다.

• PyTorch의 메서드를 외우는 것보다는, 필요할 때 마다 검색을 통해 찾아 활용하는 것이 좋음

• PyTorch 공식 Documentation : https://pytorch.org/docs/stable/index.html

Autograd(자동 미분 지원)

• 신경망 학습을 지원하는 PyTorch 자동 미분 엔진
• .backward() 메서드를 활용하여 BackwardPropagation을 수행하게 함

a = torch.tensor([2., 3.], requires_grad=True)
b = torch.tensor([6., 4.], requires_grad=True)
# requrires_grad : function에 대해 추적해야 할 변수라는 것을 알려줌
# True로 설정되었을 경우, gradient를 구할 때 편미분 해줘야 하는 변수임을 알림

Q = 3*a**3 - b**2

external_grad = torch.tensor([1., 1.])
Q.backward(gradient=external_grad)
# gradient : 벡터-야코비안 곱을 위한 스칼라 함수의 변화값

x.grad # x에 대한 편미분 값(함수)이 저장되어 있음
y.gard # y에 대한 편미분 값(함수)이 저장되어 있음

• Function이 Vector일 경우, Autograd의 미분은 벡터-야코비안 곱을 구하여 미분 값을 구하는 알고리즘이기 때문에 곱해줄 벡터(Gradient)를 설정해줘야 함
  • 하지만, 이를 설정하는 경우는 매우 드물기 때문에 아래 참고 사이트만 담
  • 참고 사이트 : https://tutorials.pytorch.kr/beginner/blitz/autograd_tutorial.html

알아두면 좋거나, 이해하기 어려웠던 개념

torch.matmul

• matmul Documentation : https://pytorch.org/docs/stable/generated/torch.matmul.html

두 Tensor간 행렬 연산을 수행하는 메서드로, Tensor의 Dimension에 따라 연산이 달라지는 특징을 가지고 있다.

이는 Batch Matrix Multiply를 수행하기 때문이다.

• Batch Matrix Multiply란? : https://baekyeongmin.github.io/dev/einsum/

간단히 말하자면, Shape가 (n,i,j)와 (n,j,k)인 Matrix 간 연산이 수행될 때, 수학적으로 따지면 두 행렬의 곱은 수행 될 수 없다
하지만, Batch Matrix Multiply가 적용되면 $A_{nij} * B_{njk}$ 연산을 통해 matmul 연산이 수행되는 것이다.

또한 matmul은 Broadcasting을 통해 행렬의 곱 연산을 수행하기도 한다.

위 모든 내용을 정리하여 Tensor 2개의 Dimension에 따른 matmul 연산을 확인해보자.

1. 두 Tensor가 모두 1 dimension
Dot Product를 수행한다

2. 두 Tensor가 모두 2 dimension
Matrix Product를 수행한다.

3. A * B를 수행할 때, A가 1 dimension이고 B가 2 dimension
Matrix Product를 수행해야 한다.
따라서, A의 앞 dimension에 1을 추가해 준 뒤, Matrix Product를 수행하고 다시 더해준 차원을 제거하는 방식으로 연산을 수행해준다.

4. A * B를 수행할 때, A가 2 dimension이고 B가 1 dimension
Matrix-Vector Product를 수행해야 한다.

5. 두 Tensor가 1 dimension 이상이고 1개 Tensor가 3 이상의 N dimension
Batched Matrix Multiply를 수행해야 한다.
(위 설명 참조)

예를 들어, 각각 (j,1,n,m), (k,m,p) Shape를 가지고 있다고 가정하자. 이 경우, 먼저 작은 Dimension을 지닌 Tensor에 차원을 추가한다. 즉, (k,m,p)를 (1,k,m,p)로 설정하는 것이다.
이후, Batch Matrix Multiply를 수행한다. 즉, $A_{j1nm} * B_{1kmp}$가 수행 될 것이며, 이는 결국 $C_{jknp}$의 결과가 도출될 것이다.
즉, (j,1,n,m)과 (k,m,p) Tensor의 Matmul 연산 이후의 Shape는 (j,k,n,p)가 될 것이다.

torch.gather

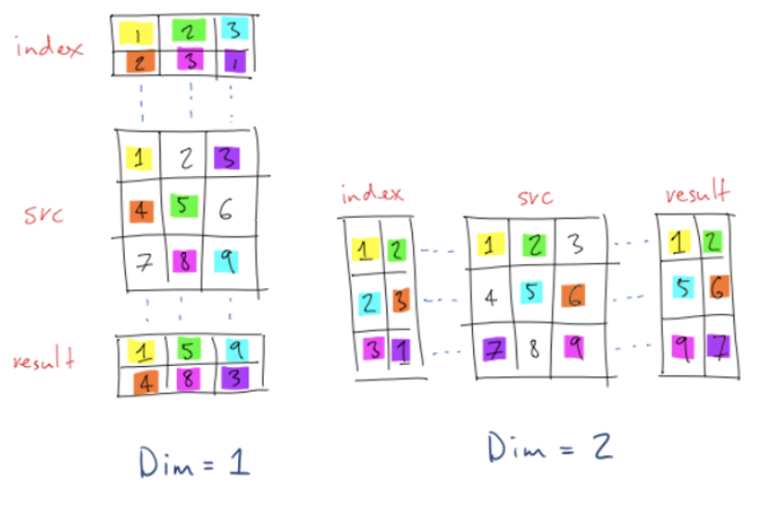
• 사진 출처 및 설명 : https://stackoverflow.com/questions/50999977/what-does-the-gather-function-do-in-pytorch-in-layman-terms

Indexing 방법 중 하나이다.
Axis와 Matrix를 지정해주어 지정해 준 Index에 존재하는 값만을 따로 빼오는 함수이다.

내가 이해한 torch.gather은 아래와 같다.

내가 설정해주는 것은 Index, 즉 거름망에 걸러지는 선택 기준이다.
또한 dim을 axis라고 생각하면 된다.
사진은 dim을 1부터 시작해서 조금 헷갈릴 수도 있지만, Axis라고 생각해도 된다.
(아마 3차원 Data에 대한 Gather를 보여주기 위해 1,2로 dim을 지정해줬던 것 같다.)
편의상 dim = 1을 axis = 0인 Case로, dim = 2를 axis = 1인 Case로 생각하자
(즉, 2차원 Data라 생각하고 gather를 이해해보자)
또한, 그림은 편의를 위해 index를 1부터 시작했지만, torch.gather의 index는 0부터 시작한다.

dim = 1인 경우를 살펴보자. Axis = 0 Case로 생각하자고 했으니, 우리가 지정한 Index(거름망)은 위 아래로 움직이게 될 것이다.
이 때 거름망이 위 아래로 움직이면서 해당하는 Index를 선택하게 되는 것이다.
예를 들어, index[0,0]에 1이 저장되어 있을 것이다.
이 때는 거름망은 위아래로 움직이므로, 해당 거름망은 (1, 4, 7) 중
1개 Data를 걸러 해당 영역에 저장시킬 것이다. 그리고, 해당 영역 중 "첫번째 Data"를 뽑는 것이므로, 1이 뽑히는 것이다

dim = 2인 경우 또한 Axis = 1 Case로 생각하여 거름망이 좌우로 움직인다 생각하면 이해하기 쉬울 것이다.

• 코드를 통한 torch.gather 이해

import torch

def get_diag_element_3D(A):
    x = A[0].shape[0]
    y = A[0].shape[1]
    
    if(x<y):
        index = torch.arange(x).expand(A.shape[0],x).unsqueeze(2)
        output = torch.gather(A,2,index).squeeze()
    else:
        index = torch.arange(y).expand(A.shape[0],y).unsqueeze(1)
        output = torch.gather(A,1,index).squeeze()

    return output

먼저, 위 코드를 설명하기 전에 미리 설명해야할 것이 있다.
주로 Data Input을 받을 때, (A,B,C)일 경우 (B,C)의 Data가 A개 존재한다의 형식으로 많이 주어진다.
(이 경우, 대부분 A가 Batch Size를 의미한다)
따라서, 우리가 실제로 Gather를 사용할 때는 A = 1인 Case, 즉 1개 층에 대해서만 Gather 함수 적용을 어떻게 할지 고민한 이후 이렇게 구한 거름망을 A 개수만큼 만들어 gather를 수행하면 될 것이다.
(B, C에 대해서만 적용하고, Batch Size만큼 해당 연산을 복사해준다고 생각하면 편하다)

위 코드는 대각 요소를 가지고 오는 코드이다.
나는 A[0,0], A[1,1], ..., A[N,N]을 가지고 오고 싶다.
A의 shape가 (x,y)일 때, x < y인 Case만 고려해보자.

A[0,0], A[1,1], ..., A[x,x] 까지의 Data가 대각행렬이 될 것이다
그렇다면 x축 방향으로 움직이는게 편할까, y축 방향으로 움직이는게 편할까?

사실 그렇게 큰 차이는 없을 것이다. x축 방향으로 움직이든 y축 방향으로 움직이든 x 크기로 거름망을 만들면 자동으로 Index = 0부터 시작하도록 맞춰지기 때문에 문제 없다.

하지만, 이왕이면 거름망 크기와 이동하는 Axis 크기가 같은 것이 기분이 좋기 때문에, 좌우로 움직이는 걸로 해보자

좌우로 움직이므로, Axis = 2로 설정해야 할 것이다
(잊지말자. A의 한 층만 생각하여 구한 거름망을 높이만큼 복사하는 방식을 활용하여 2차원으로 생각하는 것이지만, A는 3차원이다!)

먼저, A[0,0], A[1,1]..., A[x-1,x-1] 값을 불러 내야 하므로, 거름망에는 [0,1,...,x-1] 값이 존재해야 할 것이다.
따라서, 먼저 torch.arrange(x)로 1개 층의 거름망을 만들어준다.

아까 말했듯, 이렇게 만든 거름망을 층 개수만큼 복사해야 하므로,
expand명령어를 통해 A.shape[0]만큼 거름망을 만들어준다.
(거름망 크기 : A.shape[0] * x)

마지막으로, 거름망과 데이터의 Channel 개수는 같아야 하므로 3차원으로 맞춰줘야 하고, 우리는 Axis = 2방향으로 움직이므로 unsqueeze(2)를 통해 축을 하나 추가시켜주자.

이후 gather(A,2,index)로 데이터를 모은 다음, 추가시켜줬던 축을 다시 삭제시기 위해 squeeze() 명령어를 사용하면 종료되는 것이다

Contiguous

PyTorch에는 Reshape() 메서드와 View() 메서드가 존재한다.
그리고 두 메서드가 수행하는 로직 자체는 동일하다(Dimension 변화)

교수님께서는 view() 메서드 사용을 추천했지만, 과연 어떤 차이가 존재할까?

답부터 말하면 변형시킬 Tensor객체가 "Contiguous" 하지 않을 경우 에러가 발생하는가 아닌가에 차이가 존재한다.

view() 메서드 같은 경우 Tensor객체가 Contiguous할 경우에만 코드가 수행되며, 아닐 경우 에러가 발생한다.

반대로 reshape() 메서드는 Tensor 객체가 Contiguous할 경우 input의 view를 반환하지만, 아닐 경우 Contiguous한 tensor로 Copy한 이후 view 결과값을 반환한다

Contiguous란 무엇인가? 처음 선언될 때 새로운 메모리 주소로 할당되었는지, 원래 존재하던 메모리 주소를 재활용하는지 여부를 판단해주는 개념이다

transpose() 메서드 같은 경우 Tensor객체를 변형시키지 않고, 단지 Tensor객체의 메모리 주소 접근 순서만 바꿔 출력하는 형식을 선택한다.

즉, transpose() 메서드로 만들어진 객체는 새로운 공간에 할당된 것이 아닌, 이미 할당된 tensor 객체를 재활용하는 것에 불과하다.
이런 경우를 "Contiguous 하지 않다"라고 한다.

• 코드를 통한 이해

import torch

x = torch.tensor([[1, 2, 3], [4, 5, 6]], dtype=torch.int32)

# 1번 : view() 메서드를 수행해보자
x.view(-1,6)
"""
결과 : [[1,2,3,4,5,6]]. 
x는 자신만의 메모리를 갖고 선언된 Tensor객체이므로  Contiguous하다.
즉, view 메서드 활용이 가능하다
"""

# 2번 : reshape() 메서드를 수행해보자
x.reshape(-1,6)
"""
결과 : [[1,2,3,4,5,6]]. 
x가 Contiguous할 경우, view() 메서드를 수행시킨다고 했다.
즉, 1번 과정과 "완전히 같은" 연산이 수행된다.
"""

# 3번 : 정말로 같은 연산이 일어났을까? 깊은 복사와 얕은 복사 차이가 있는지
# 확인해보자!
y = x.view(-1,6)
z = x.reshape(-1,6)
x.fill_(1) 
y==z
# 결과 : [[True, True, True, True, True, True]], 모든 원소가 같음

# 4번 : 그럼 Contiguous하지 않은 객체에 View를 수행해보자
y = x.t() # transpose()는 Contiguous하지 않는 객체를 만드는 대표적 메서드이다.
y.view(-1,6)
"""
결과 : RuntimeError. ~~~라고 나오지만, 
결국 "contiguous subspaces"부분에 집중하자
y가 contiguous하지 않으니 view() 메서드 사용이 불가하다.
Use .reshpae instead 라고 친절히 대안도 설명해준다.
"""

# 5번 : 그럼 추천대로 reshape 명령을 수행해보자.
y.reshpae(-1,6)
# 결과 : [[1, 1, 1, 1, 1, 1]]. 
# Contiguous하지 않은 객체여도 Reshape 명령은 수행됨을 알 수 있다!

"""
6번 : 마지막 수행. Reshape 명령의 경우 Contiguous하지 않은 
객체는 Contiguous 객체로 만든 이후 view() 메서드를 수행한다고 한다.
즉, 다른 공간에 메모리를 할당한 이후 Contiguous하지 않은 객체를 Copy하여 객체를 
새로 생성하는 것이다
이는 다르게 말하면, 원래 존재하는 객체를 깊은 복사한 것과 비슷한 연산으로 원래 
Tensor객체의 변동 영향을 받지 않을 것이다.
실제로 이 과정이 수행되는지 알아보자!
"""
y = x.view(-1,6)
z = x.t().reshape(-1,6)
x[0,0] = 0
y,z
"""
결과 : y - [[0, 1, 1, 1, 1, 1]], z- [[1, 1, 1, 1, 1, 1]]
y는 view() 메서드로 Contiguous한 x 형태를 바꾼 것이다.
즉, 메모리를 공유하기 때문에 x tensor값이 바뀌면 y값도 바뀌게 될 것이다.
하지만, z 같은 경우 x.t()가 UnContiguous하기 때문에 새로운 공간에 Copy한 이후
view()를 수행한다
즉, z와 x는 다른 주소값을 가지는 것이다
따라서, x.t().reshape()를 수행한 순간 z와 x는 관련 없는 행렬이므로
z의 값은 변경되지 않는 것이다
"""