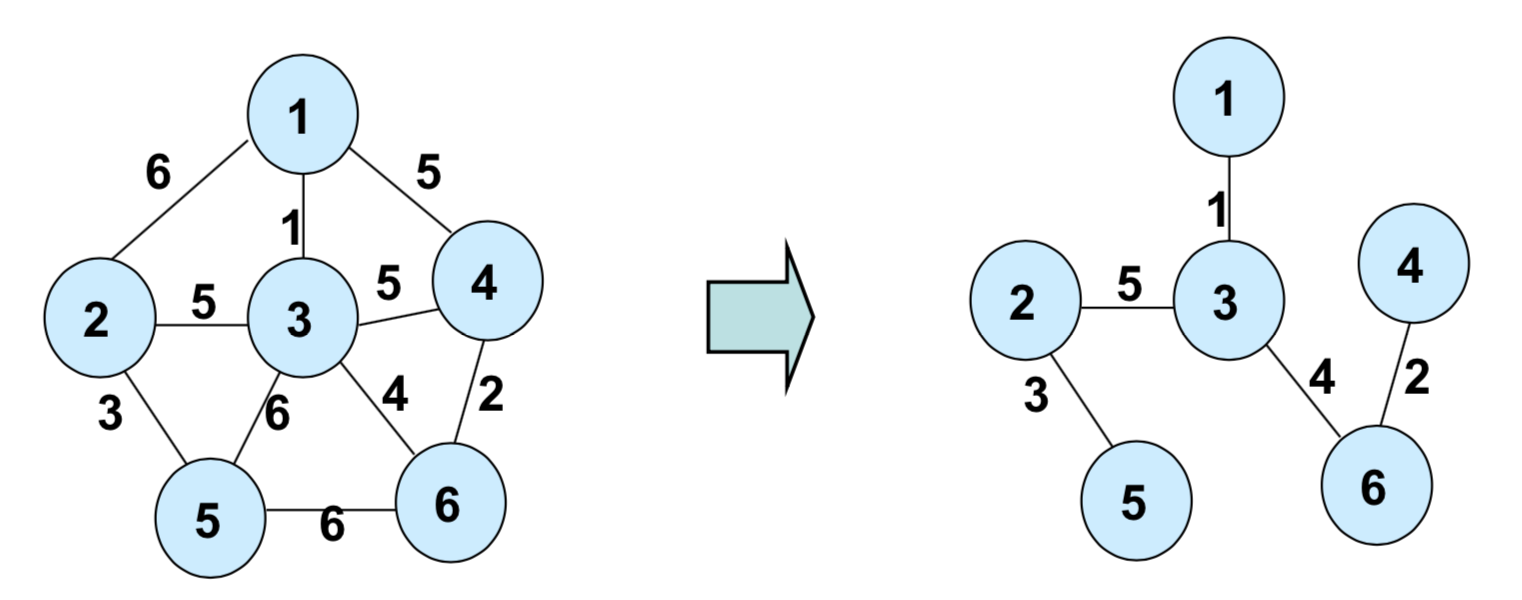
그래프

이종찬·2023년 5월 18일

알고리즘

그래프

그래프는 Node, Edge로 구성된 집합입니다. Node는 데이터를 표현하는 단위이며, Edge는 Node를 연결합니다.

구현 방법

1. Edge list

에지를 중심으로 그래프를 표현하며 배열에 출발 노드, 도착 노드를 저장하거나 가중치를 저장하여 가중치가 있는 에지를 표현할 수도 있습니다.

이미지 참조 링크

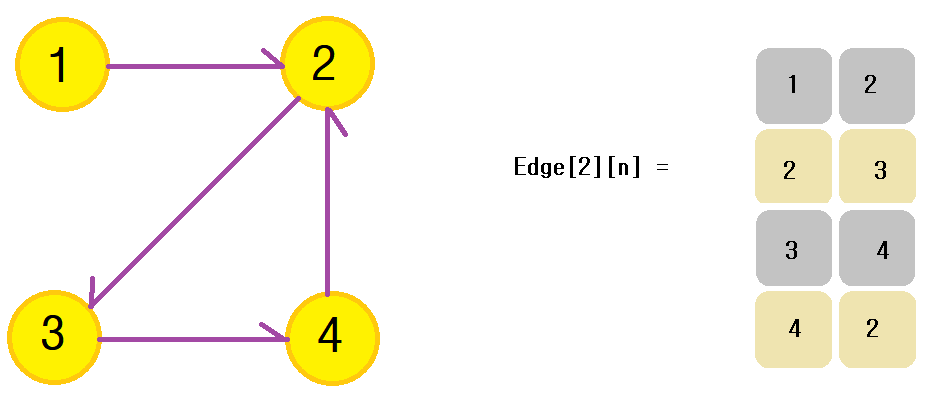
가중치가 있는 그래프는 행을 3개로 늘려 3번째에 가중치를 저장하면 됩니다.

위의 그림처럼 쉽게 구현이 가능하지만 특정 노드와 관련되어 있는 에지를 탐색하기는 쉽지 않습니다. 밸만-포드, 크루스칼과 같은 알고리즘에 사용되며 노드 중심 알고리즘에는 잘 사용되지 않는 특징을 가지고 있습니다.

2. 인접 행렬

인접 행렬은 2차원 배열을 자료구조로 이용하여 그래프를 표현하는 방식입니다. 위에서 나온 Edge list와 다르게 노드 중심으로 그래프를 표현합니다.

가중치 없는 그래프의 경우 1 -> 2 를 표현할 때 A[1][2] 부분에 true 또는 1과 같이 1에서 2로 향하는 에지가 있다는 것만 표시하면 됩니다.

가중치가 있는 그래프의 경우 1 -> 2 를 표현할 때 A[1][2] 부분에 가중치를 저장하면 됩니다.

장점

인접 행렬을 이용한 그래프 구현은 난이도가 쉬운 편이며, 노드와 노드사이를 연결하는 에지의 여부 및 가중치값을 배열에 직접 접근하여 바로 확인할 수 있는 것이 장점입니다.

단점

노드와 관련되어 있는 에지를 탐색하려면 N번 접근해야 하므로 노드 개수에 비해 에지가 적을 경우 공간 효율성이 떨어집니다. 또한 노드가 3만개가 넘으면 힙 메모리 에러가 발생하여 2차원 배열 선언 자체를 할 수 없는 결함도 존재합니다.

3. 인접 리스트

인접 리스트는 ArrayList로 그래프를 표현합니다. 노드 개수 만큼 ArrayList를 선언합니다.

가중치 없는 그래프

인접 행렬과 마찬가지로 1 -> 2 경우 List[1].add(2)를 하여 연결 할 수 있습니다. 차이점은 인접 행렬의 경우 한가지의 노드만 입력할 수 있지만 인접 리스트의 경우 하나의 노드에 여러개의 노드가 연결되는 것을 나타낼 수 있습니다.

가중치 있는 그래프

인접 리스트의 경우 class를 사용하여 나타낼 수 있습니다. ex) Node 라는 클래스에 파라미터가 node, value를 사용하여 다음과 같이 추가할 수 있습니다.

List[1].add(new Node(node,value))

장점

노드와 연결되어 있는 에지를 탐색하는 시간 및 공간 활용이 인접 행렬보다 뛰어납니다. 또한 수용할 수 있는 노드 개수도 더 많아 메모리 초과 에러도 발생하지 않습니다. 이러한 큰 장점이 있어 코딩테스트에서 가장 선호하는 그래프 구현 방식입니다.

단점

그래프를 구현하는 위와 같은 방법 중에 복잡한 편입니다.

유니온 파인드

union-find는 일반적으로 여러 노드가 있을 때 특정 2개의 노드를 연결해 1개의 집합으로 묶는 union연산과 두 노드가 같은 집합에 속해 있는지를 확인하는 find 연산으로 구성되어 있는 알고리즘입니다.

union연산은 각 노드가 속한 집합을 1개로 합치는 연산입니다. 노드 a,b가 각각 다른 집합에 속한 경우 union(a,b)를 사용하여 합칩니다. 합집합과 같은 개념입니다.

find연산은 특정 노드가 속한 집합의 대표 노드를 반환하는 연산입니다. a라는 노드가 A집합에 있는 경우 find(a)를 사용하여 a노드가 속한 집합의 대표 노드를 반환합니다.

구현 방법

이미지 참조 링크

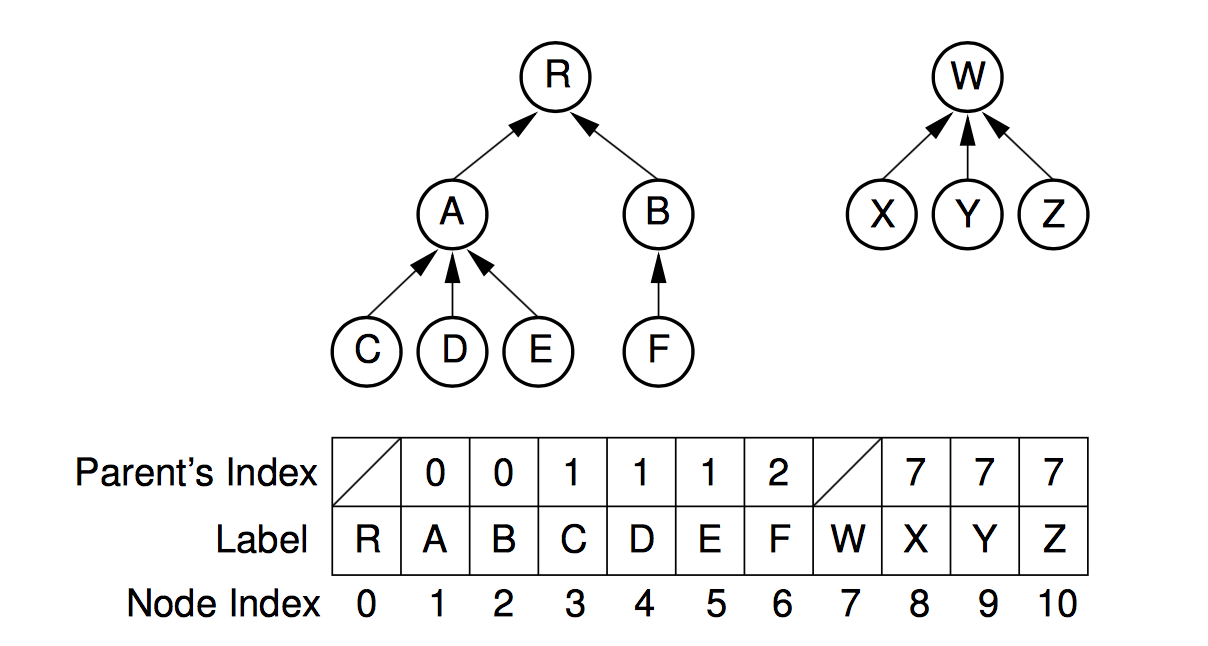
union-find를 표현하는 일반적인 방법은 1차원 배열을 사용하는 것입니다.

초기에 1차원 배열을 각 노드가 대표 노드가 되도록 인덱스값을 초기화해줍니다.
2개의 노드를 선택해 각각의 대표 노드를 찾아 연결하는 union 연산을 수행합니다. ex) union(a,b)인 경우 b의 A[b] = b -> A[b] = a가 됩니다.
find 연산으로 자신이 속한 집합의 대표 노드를 쉽게 찾을 수 있으며 시간 복잡도 향상의 효과도 있습니다.

위상 정렬

은 사이클이 없는 방향 그래프에서 노드 순서를 찾는 알고리즘입니다.

위상 정렬(topology sort)은 비순환 방향 그래프(DAG)에서 정점으로 선형으로 정렬하는 것이며 모든 간선과 노드(a,b)가 있을 때 a가 b보다 먼저 오는 순서로 정렬됩니다.

주의 할점

위상 정렬은 항상 유일한 값으로 정렬되지 않습니다. 또한 사이클이 존재하면 노드 간의 순서를 명확하게 정의할 수 없으므로 위상 정렬을 적용할 수 없습니다.

구현 방법

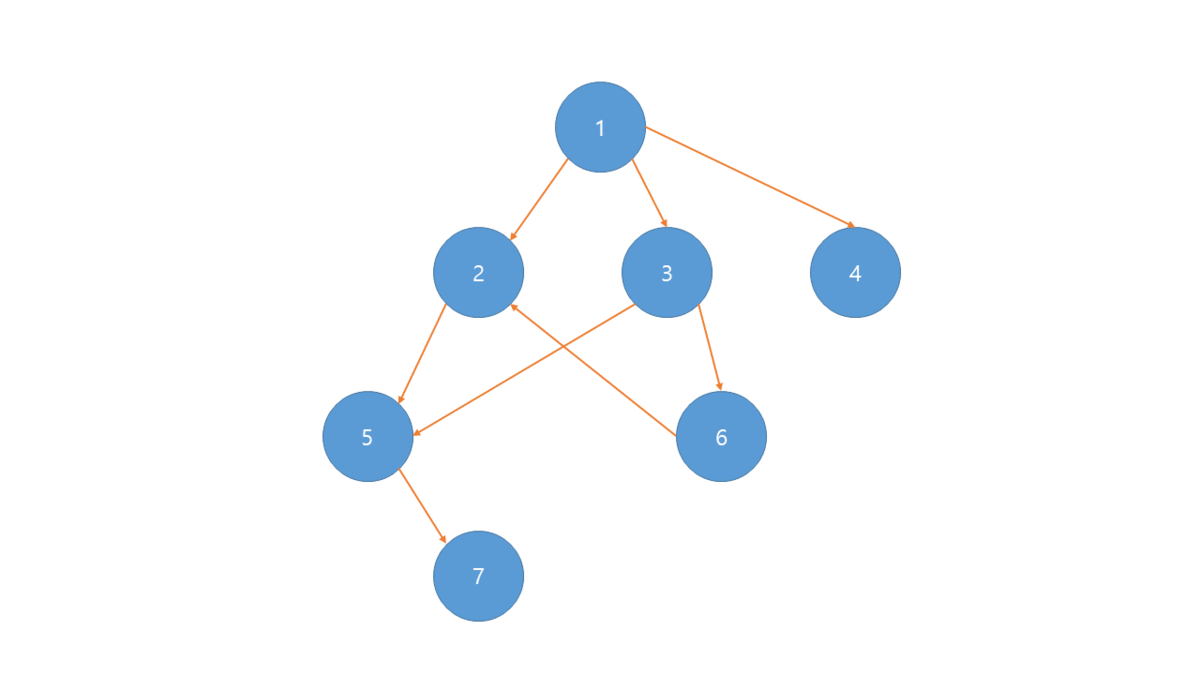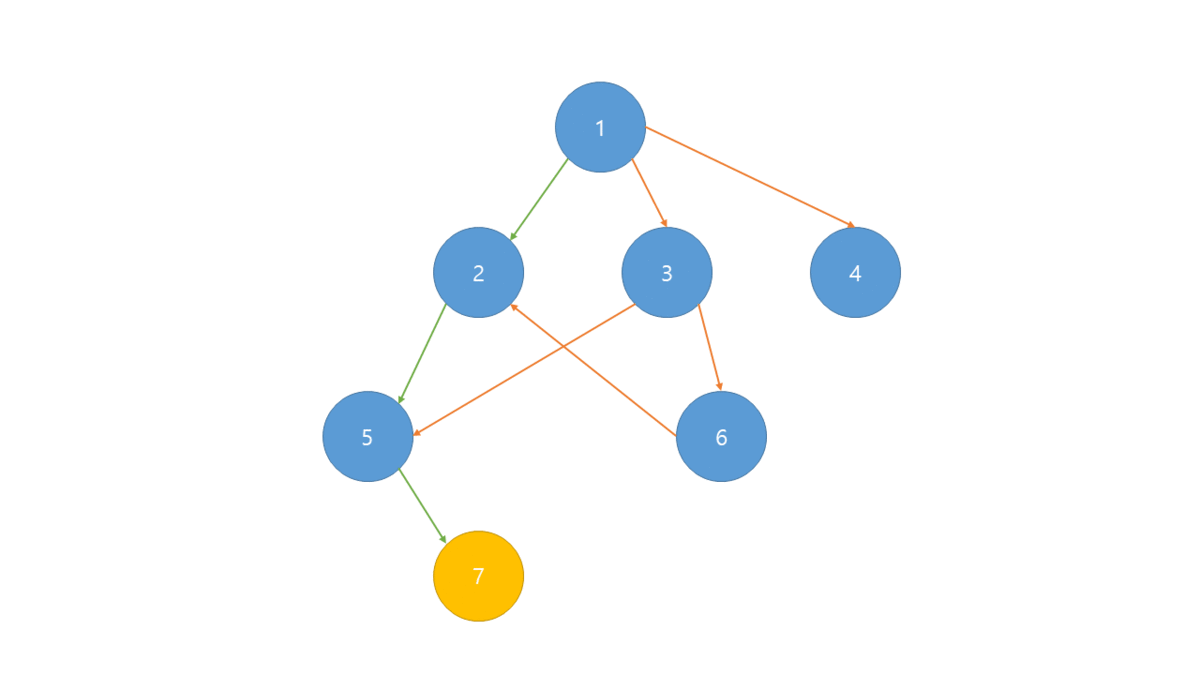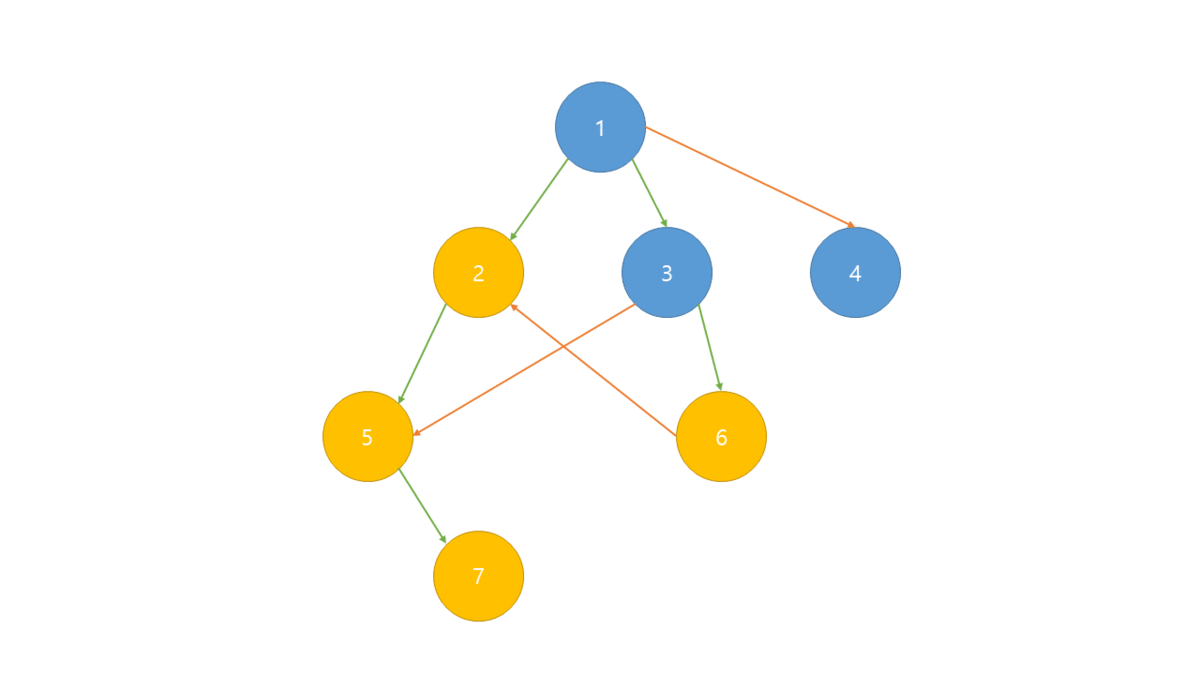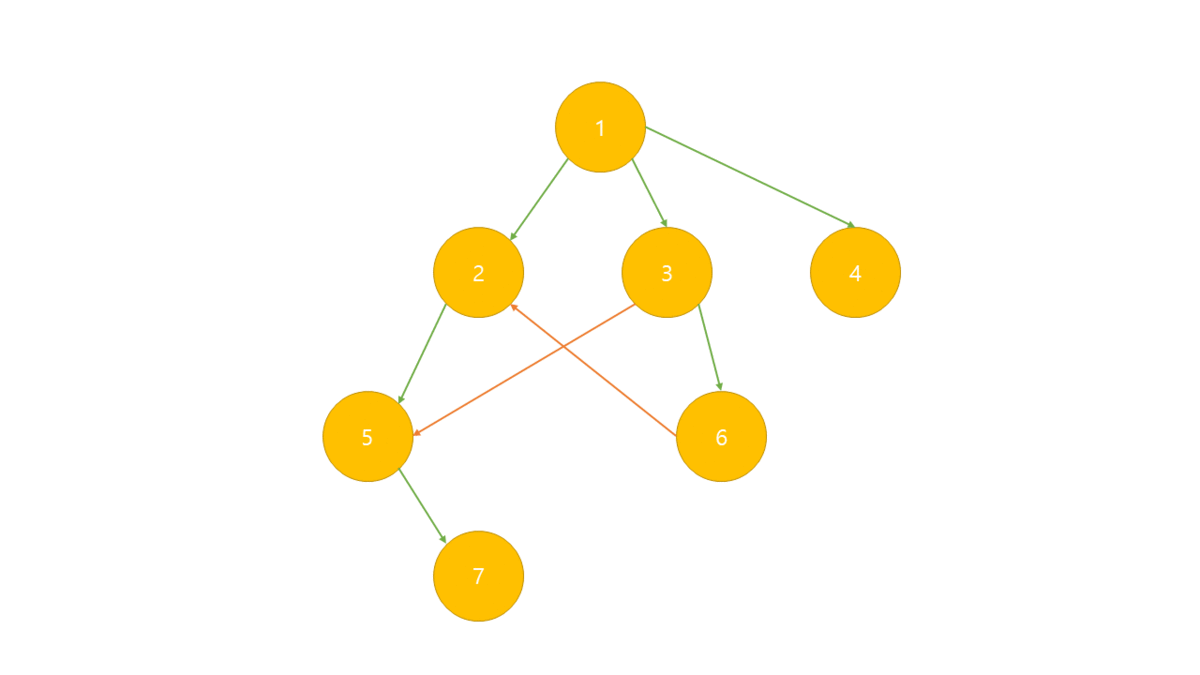
위상정렬은 각 노드별 진입차수(자기 자신을 가리키는 Edge의 개수)를 나타내는 진입 차수 배열이 필요합니다.

진입 차수 배열중 0의 값이 루트이며 진입 차수를 증가 반복하여 출력합니다.

BFS로 그래프의 진입 차수 배열 생성
진입 차수가 0인 노드를 선택하여 정렬 배열에 저장 및 큐에서 제거
인접 리스트에서 선택된 노드가 가리키는 노드들의 진입 차수 -1
위의 2,3과정을 반복 하며 더 이상 반복 할 수 없는 경우 정렬 배열 출력.

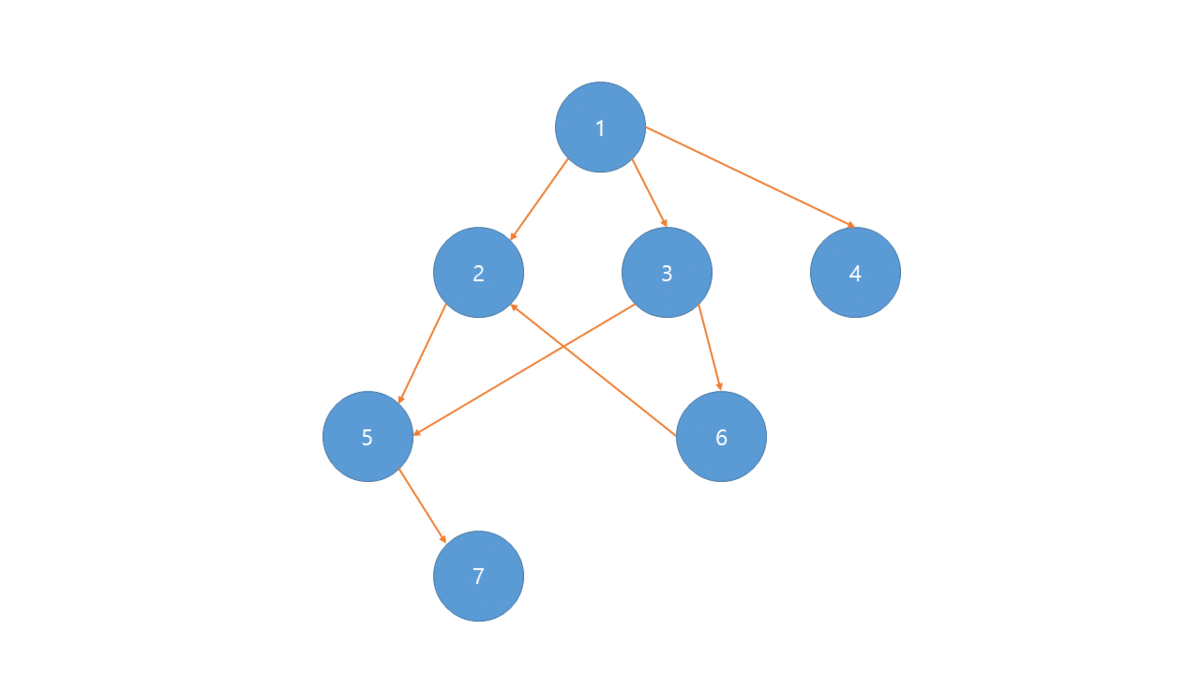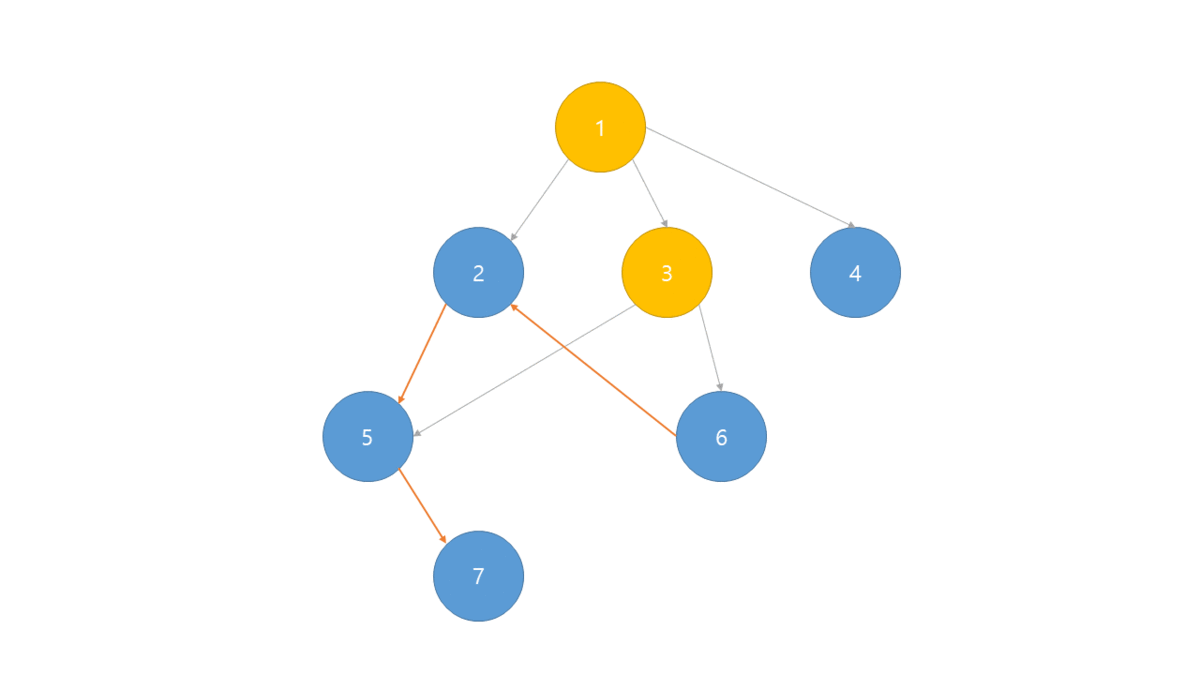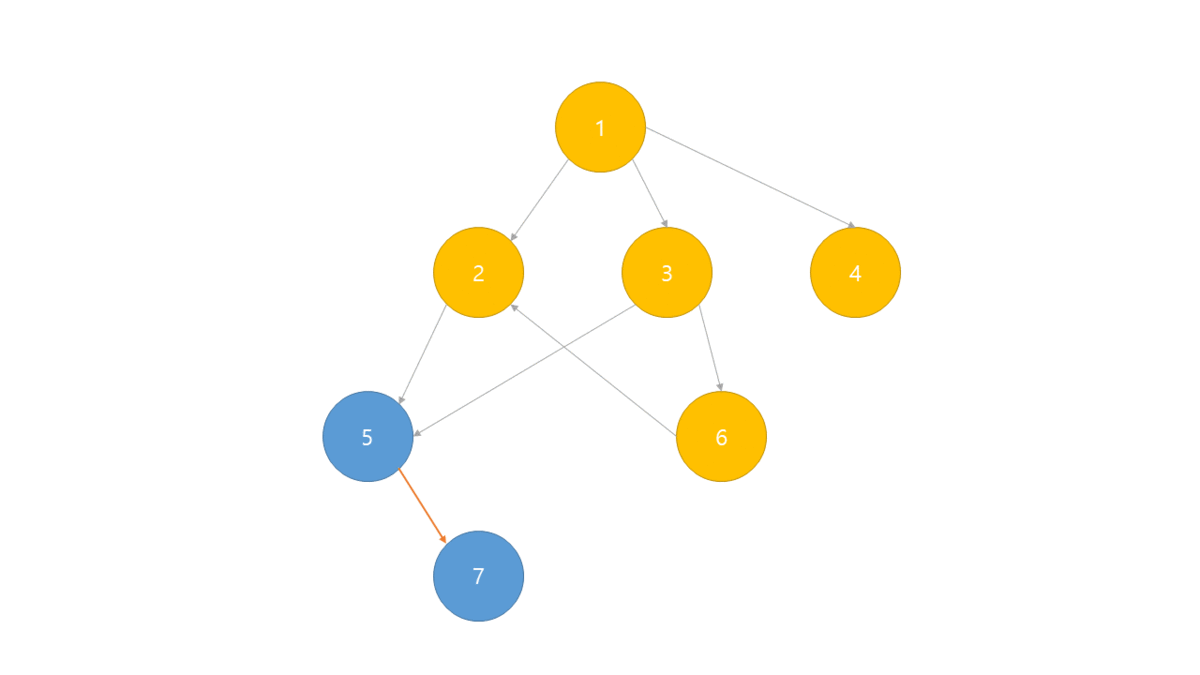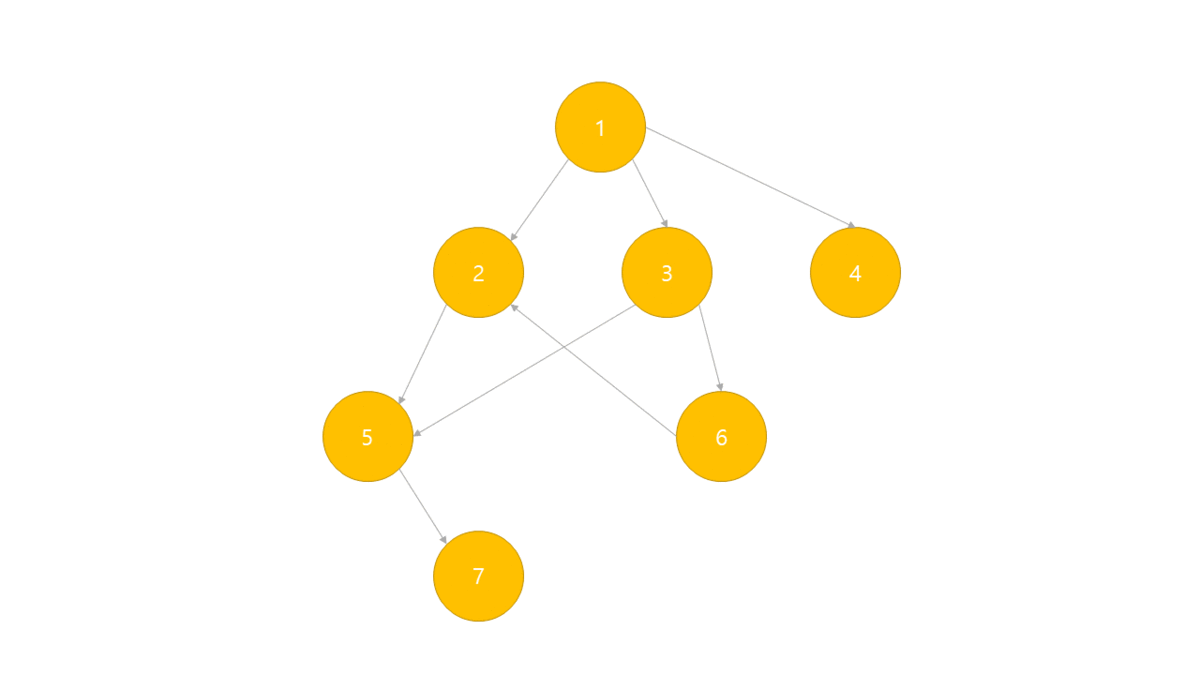
만일 DFS를 사용한다면 역순으로 정렬되게 됩니다.

이미지 참조 링크

다익스트라

다익스트라 알고리즘은 그래프에서 최단 거리를 구하는 알고리즘입니다. 특정 노드에서 다른 노드들의 최단 거리를 구하는 문제를 푸는 것에 적합한 알고리즘입니다.

구현 방법

인접 리스트를 사용하여 Node클래스에 (node, value)를 형태로 선언하여 생성해줍니다.
최단 거리 배열을 만들고 출발 노드 이외의 노드는 문제에서 나올 수 있는 최대값으로 초기화 해줍니다.
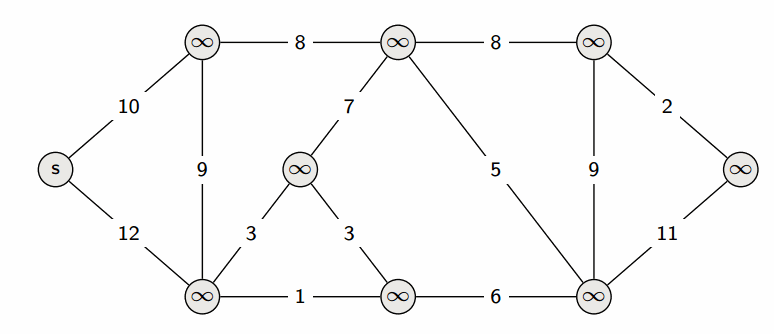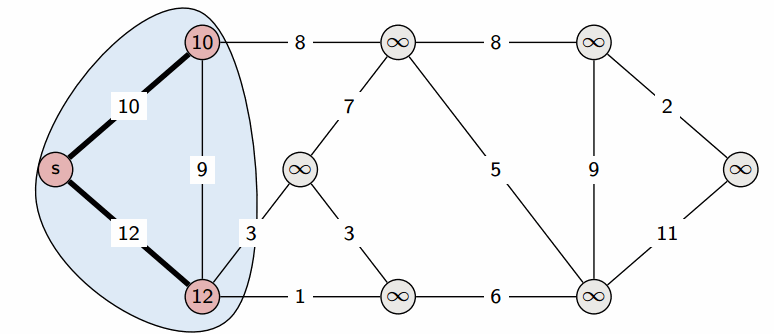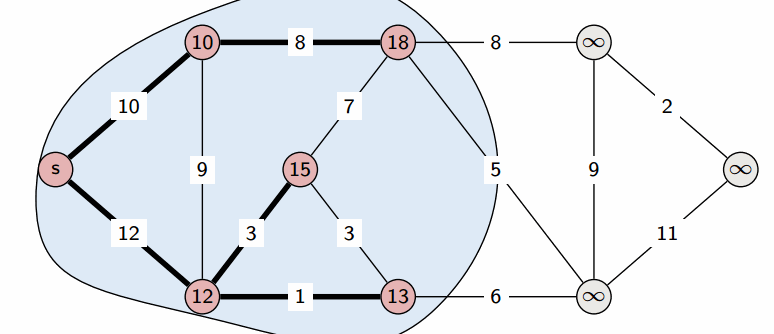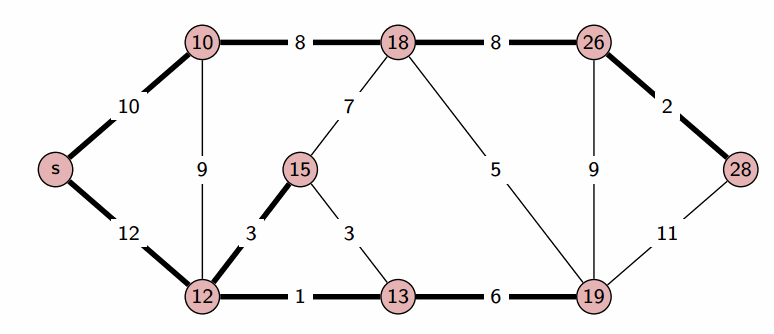
최단 거리 배열에서 현재 값이 가장 작은 노드를 선택합니다.
선택된 노드에 연결된 값을 바탕으로 다른 노드의 값을 업데이트 합니다(작은 값으로).
3,4 과정을 반복하여 최단 거리 배열을 완성시키면 됩니다.

이미지 출처 링크

플로이드-워셜

플로이드-워셜 역시 그래프에서 최단 거리를 구하는 알고리즘입니다. 가장 핵심적인 원리는 A노드에서 B노드까지 최단 경로를 구했다는 가정하에 새로운 C노드가 최단 경로 위에 있다면 해당 부분 역시 최단경로입니다.

ex) A -> B -> C 에서 A -> C가 최단 경로인 경우 A -> B라는 최단 경로와 B -> C라는 최단 경로로 이뤄진다는 의미

위와 같은 내용을 기반으로 다음과 같은 점화식이 나올 수 있습니다.

D[A][C] = Math.min(D[A][C], D[A][B] + D[B][C])

구현 과정

D[A][C]는 노드 A에서 C까지 최단 거리를 저장하는 배열이라 정의합니다. A,C는 각각 0, INF로 초기화해줍니다. (A == C는 자기 자신에게 가는데 걸리는 최단 경로값을 의미)
출발 노드 S, 도착노드 C, 가중치 W라고 했을 때 D[A][C] = W로 간선의 정보를 배열에 입력합니다. (해당 알고리즘은 그래프를 인접 행렬로 표현)
기존에 구했던 점화식을 3중 for문의 형태로 반복하면서 배열의 값을 업데이트합니다. 완성된 배열은 모든 노드 간의 최단 거리를 나타냅니다.

위와 같은 과정에 시간 복잡도는 O(V3)로 속도가 빠른 알고리즘은 아닙니다. 해당 알고리즘은 사용하는 문제는 입력값이 매우 범위가 적으며 단순 최단거리가 아닌 모든 경우를 다 확인할 때 사용됩니다.

최소 신장 트리

최소 신장 트리는 그래프에서 모든 노드를 연결할 때 사용된 간선들의 가중치의 합을 최소로 하는 트리입니다.

노드가 아닌 간선 중심으로 저장하므로 인접 리스트가 아닌 EdgeList 형태로 저장하게 됩니다. 최소 신장 트리를 구성하는 노드가 N개라면 간선의 개수는 항상 N - 1개 이며 사이클이 포함되지 않는 그래프에 사용됩니다.

구현 과정

EdgeList 형태로 그래프를 구현하고 union-find 배열을 초기화 해줍니다. 이 때 Edge 클래스에는 노드 변수 2개와 가중치 변수로 구성됩니다.
EdgeList에 담긴 데이터를 가중치 기준으로 오름차순 정렬합니다.
가중치가 낮은 Edge부터 순서대로 선택해 연결을 시도합니다. 그래프의 사이클 여부를 find 연산을 이용하여 확인한 후 사이클이 형성되지 않는 경우에만 union 연산을 사용해 두 노드를 연결합니다.
3의 과정을 전체 노드 개수(N) - 1 = E 이 될 때 까지 반복해줍니다.
완성된 최소 신장 트리의 총 가중치의 합을 출력합니다