정수론
정수론은 정수와 관련된 수학적 성질과 정리를 다루는 학문입니다. 코테에서는 주로 소수를 구하여 주어진 문제를 해결하는 방식이 많습니다.
소수
자신보다 작은 2개의 자연수를 곱해 만들 수 없는 1보다 큰 자연수를 의미합니다. (1과 자기 자신 외의 값이 존재하지 않는 수)
에라토스테네스의 체
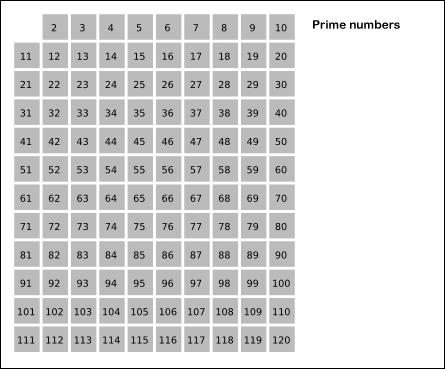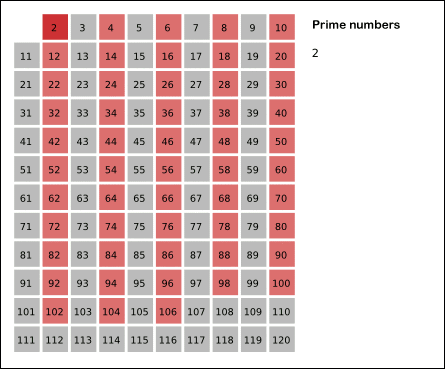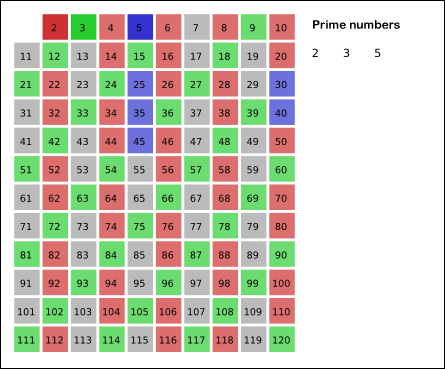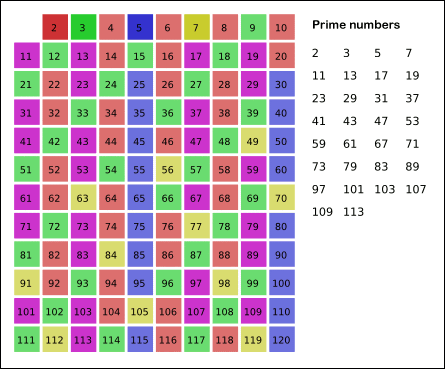
코딩테스트에서 소수를 구하는 대표적인 판별법으로 다음과 같은 과정을 반복합니다.
- 입력 받은 수의 범위 만큼 2부터 탐색합니다.
- 선택된 수의 배수를 모두 삭제합니다.
- 다음으로 지워지지 않은 수를 선택하여 2번의 과정을 N(주어진 길이)까지 반복합니다.
- 삭제되지 않은 수를 모두 출력합니다.
해당 알고리즘의 시간 복잡도는 이중 loop를 사용하여 O(N2)로 판단할 수 있지만 실제로 최적화에 따라 O(Nlog(logN))로 나올 수 있습니다. 배수를 삭제하는 연산에서 반복문을 생략하는 경우가 많기 때문입니다. 예를 들면 a * b = N 이라는 가정하에 a,b <= N의제곱근 이라는 공식이 나옵니다.
ex) N=16 -> 1 16, 2 8, 4 4, 8 2, 16 * 1
N의 제곱근을 기준으로 이전에 수식이 반복되는 것을 확인할 수 있습니다. 이로 인해 전체 탐색할 필요없이 N의 제곱근 까지만 탐색해도 전체를 탐색하는 효과를 얻을 수 있습니다.
오일러 피
코테에서 나오는 오일러 피 함수의 A[N]의 정의는 1~N까지 범위에서 N과 서로소인 자연수의 개수를 의미합니다. 세부적으로 들어가면 이해하기 어렵지만 부분적인 내용만 익힌다면 코테에서 구현할 수 있습니다.
ex) 1부터 6까지의 수 중에 6과 서로소인 수의 개수를 구해야 하는 경우
- 1~6까지 수 중에 6 % K(소수) == 0 가 되는 수를 찾습니다.
- 해당 수를 찾았으면 수의 배수인 값을 찾아 제거합니다.
- 배열의 길이만큼 1,2 과정을 반복해줍니다. (제곱근까지만 해도 됨)
위의 과정을 거치면 1,5만 남게 되며 서로소의 개수가 2개가 나오는 것을 알 수 있습니다.
이러한 과정의 공식은 A[i] = A[i] - A[i] / K로 나타낼 수 있습니다.
많은 수학적인 부분을 건너뛰었지만 서로소를 구하는 문제를 해결할 때 아주 유용하게 사용할 수 있습니다.
유클리드 호제법
두 수의 최대 공약수를 구하는 알고리즘입니다. 소인수분해를 이용하여 공통된 소수들의 곱으로 표현이 가능하지만 유클리드 호제법은 보다 더 간단한 방법으로 문제를 해결합니다.
과정
유클리드 호제법에서는 MOD(%) 나머지 연산을 사용합니다.
- 큰 수(A)를 작은 수(B)로 나누는 MOD 연산 수행 -> ex) 270 % 192 -> 78 , A MOD B -> C
- 1번 과정에서 도출된 B와 C를 가지고 나머지 연산을 수행 -> ex) 192 % 78 -> 36 , B MOD C -> D
- 위의 과정을 나머지가 0이 될 때까지 반복 -> 78 % 36 -> 6 , 36 % 6 -> 0
- 연산 결과가 0이 될 때 사용된 작은 값이 최대 공약수 결과 도출

