[PythonBasic] Stack & Queue

Stack & Queue

Stack

LIFO (Last In First Out)

• 가장 최근에 쌓인 데이터가 가장 먼저 처리된다.
• 마치 설거지를 할 때에, 완료된 그릇들을 차곡차곡 건조대에 쌓아올리고 이후에 가장 위에 쌓아진 그릇부터 사용되는 것과 같다.
• Stack에서 데이터 저장은 push, 데이터를 읽어들이는 건 pop 이라고 함. (다만 pop은 읽어들임과 동시에 stack에서 삭제)
• 장: 구조가 단순, 구현이 쉬움, 데이터 저장과 불러오기 속도가 빠름
• 단: 데이터 최대갯수 사전에 지정 필요, 저장 공간 낭비 발생 가능(리스트와 비슷)
  --> 이러한 단점 때문에 보통 리스트로 대체하여 사용, 즉 파이썬에서는 스택을 따로 구현할 필요는 없음

• When to use stack
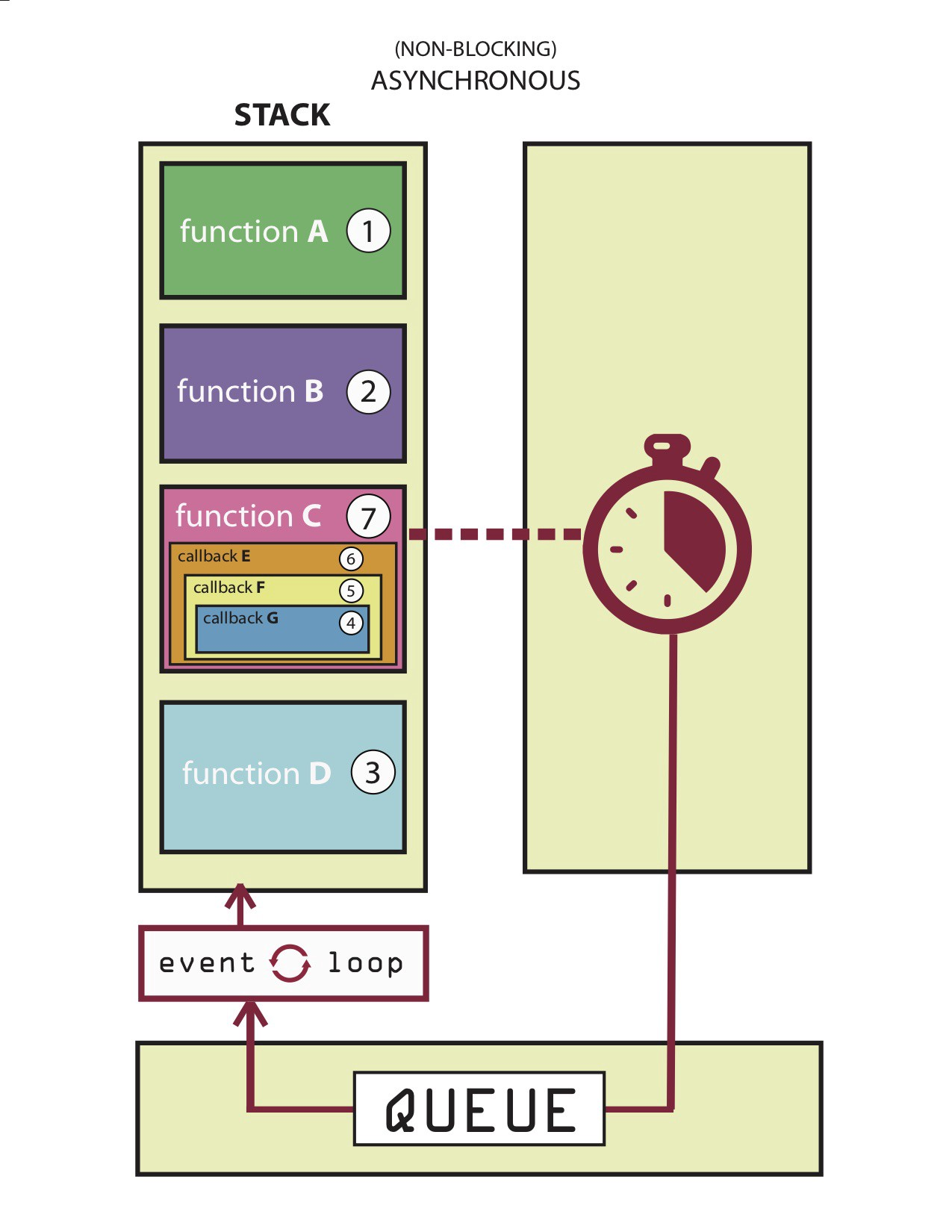
  1) 프로그램에서는 함수 호출 기록을 stack으로 저장 (그래서 StackOverflow에러 라는 것도 있는것! 프로그래밍계의 지식인 사이트 이름도 stackoverflow.)
  2) Web browser 내역 중 최신 내역이 먼저 나와야 하는 경우

Stack Code를 list로 구현해보자

 class Stack:
   def __init__(self):
     self._stack = [] # stack 인스턴스 하나를 _stack이라고 함 

   def push(self, data):
     self._stack.append(data)

   def pop(self):
     if len(self._stack) == 0:
       return None

     data = self._stack[-1]
     del self._stack[-1]

     return data

   def getPeak(self):
     if len(self._stack) == 0:
       return None

     data = self._stack[-1]

     return data

Queue

FIFO (First In First Out)

• 가장 먼저 쌓인 데이터가 가장 먼저 처리된다
• 데이터를 넣는 연산은 put, 빼는 연산은 get이라고 함
• 파이썬에서는 queue 라이브러리를 제공하나, 대부분의 큐와 관련된 자료구조는 list를 통해서 구현이 가능
• 멀티 태스킹을 위한 프로세스 스케쥴링 방식에 사용된다
• 일반적으로 FIFO 방식이나 LIFO queue도 존재한다. (LifoQueue() 사용 시)

• When to use queue
  1) 맛집 예약 시스템
  2) OS 프로세스 스케쥴링 시스템 (priority queue 사용)
  3) JavaScript 비동기 처리 (ex. DOM Event, setTimeout, HTTP 통신을 하는 fetch 함수 등..)
  

Queue Code를 list로 구현해보자

class Queue:
    def __init__(self):
        self._queue = []

    def push(self, data):
        return self._queue.append(data)

    def pop(self)
        if len(self._queue) == 0:
            return None

        return self._queue.pop()

    def getFirst(self):
        if len(self._queue) == 0:
            return None

        return self[0]

🌚 Queue는 효율성이 떨어지는 문제를 가지고 있다

stack = []
stack.append(1)
stack.append(2)
stack.append(3)
stack.pop() 	# 3
stack.pop() 	# 2
stack.pop() 	# 1 

스택은 위에서 보다시피 효율성에 큰 문제를 일으키지 않는다. 다만 문제는 큐.

queue = []
queue.append(1)
queue.append(2)
queue.append(3)
queue.pop(0) 	# 1
queue.pop(0) 	# 2
queue.pop(0) 	# 3

가볍게 보일 수도 있겠으나, 이 과정은 다음과 같은 속 사정을 가지고 있다.

0x01 0x02 0x03
[1] - [2] - [3]

0x01 0x02 0x03
[Null] - [2] - [3]

0x01 0x02 0x03
[2] - [3] - [?]

즉, 앞에서 하나를 비우고 뒤에 있는 모든 데이터들을 한 칸씩 앞으로 당기는 작업을 수반하며
가장 앞에 있는 데이터를 끄집어내는데 걸리는 시간 복잡도가 O(1)이 아니라 O(n)이 되는 현상이 벌어지는 것

빅오(Big O) 표기법이란

빅오(Big-O)는 알고리즘의 성능을 수학적으로 표시하는 대표적인 방법으로, 시간 복잡도를 표현하기 위해 사용한다. 단, 알고리즘의 실제 러닝 타임을 표시하는 것이 아니며, 인풋 데이터(혹은 사용자) 증가율에 따른 알고리즘의 성능을 예측하기 위해 사용한다. 빅오 표기법에는 다음 2가지 규칙이 있다.

1) 가장 높은 차수만 남긴다.
O(n² + n) -> O(n²)

2) 계수 및 상수는 과감하게 버린다.
O(2n + 3) -> O(n)

• O(1)의 경우 입력 데이터의 크기에 상관 없이 언제나 일정한 시간이 걸리는 알고리즘을 나타낸다. 데이터가 얼마나 증가하든 성능에 거의 영향을 주지 않는다.
• O(n)의 경우 입력 데이터의 크기에 비례해 처리 시간이 증가하는 알고리즘이다. 예를 들어 데이터가 10배가 되면, 처리 시간도 10배가 된다. 선형 탐색 알고리즘이 대표적이다.

그러니깐 결국 시간 복잡도가 O(1)이 아닌 O(n)이 되었다는 건 시간 복잡도가 증가하여 효율도가 상당히 떨어진다는 소리!

그래서 일반적으로 파이썬을 쓰는 사람들은 이와 같은 문제를 해결하기 위해
아래와 같은 코드를 선호한다.

from collections import deque 	# (*deque는 double ended queue의 약자)
queue = deque()
queue.append(1)
queue.append(2)
queue.popleft() 	# 1
queue.popleft() 	# 2

references:
https://stackoverflow.com/c/wecode/questions/212 (Eun-Woo Song)
https://davinci-ai.tistory.com/16
https://velog.io/@raram2/big-o-notation-and-time-complexity (Big O)
https://jacoblog.tistory.com/2 (Queue의 저효율 문제)