• update Feb.28.22: 오류 수정. Problems of sigmoid - Not 0 centered
• update Dec.13.22: 각 함수의 미분함수 추가

Prologue

생물이 가진 뉴런은 인공신경망보다 훨씬 복잡하게 작동한다. 그 중 '활성화'에 대한 이야기를 할 거다.

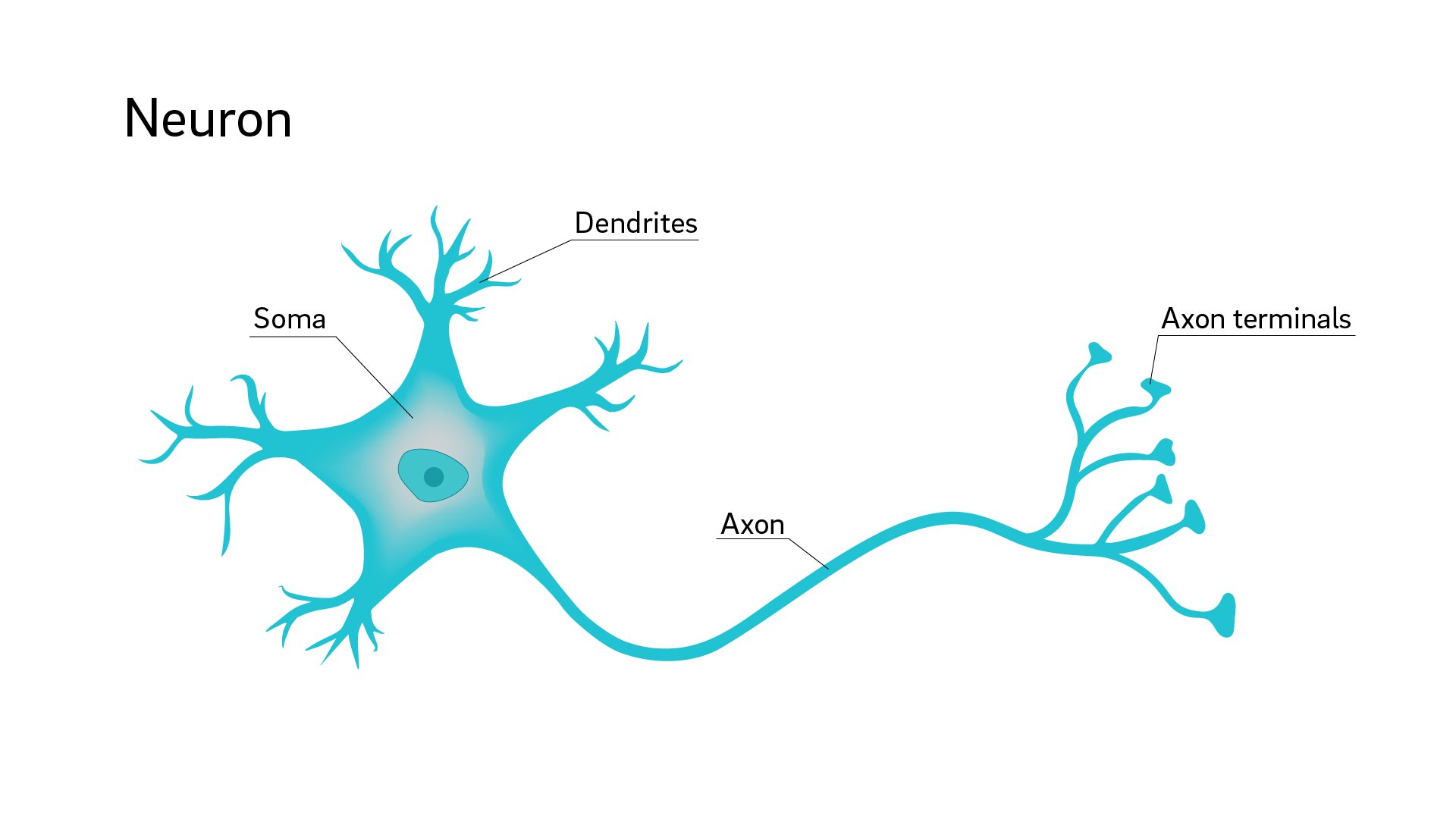
생물시간에 배웠다시피 신경세포는 이렇게 생겼다. Dendrites에서 들어온 전기신호들을 Soma에 모으고 있다가 일정강도가 되면 Axon을 통해 다른 신경세포에 전기신호를 보낸다. 이것을 신경세포의 흥분작용이라고 부른다.

이 아이디어를 인공신경망으로 가져왔다. 입력받은 신호들의 총합을 출력할지, 말지, 출력한다면 어느 정도로 출력할지 결정하는 함수를 인공신경망에서는 활성화 함수(Activation function)라고 부른다.

$g=xW+b$
$h=f(g)$

위의 식에서 입력값, 가중치와 편향의 총합을 계산한 $g$함수를 $f$함수에 넣어 $h$를 출력한다. 이때 함수 $f$가 활성화 함수다. 활성화 함수의 조건이 크게 두 가지가 있다.

1. 미분할 수 있을 것.
   이후에 최적화 기법에 쓰려면 미분할 수 있는 함수여야 한다.
2. 비선형함수일 것.
   우리가 해결해야 하는 문제는 선형함수로 분류할 수 없는 문제가 대부분이다. 만약 $f(x)=ax$모양의 함수를 써야 한다면 결과는 $axW$모양의 선형결합이라 결국 선형함수로 분류하는 과제와 같아진다.

그러면 점화식을 구현하면서 함께 알아보자.

1. Step function

모양이 계단처럼 생겼다고 해서 계단함수로 부르고 있다. 입력값이 일정 강도 이상이 되면 무조건 출력신호를 보낸다. 앞서 언급했듯 신경세포가 이런 특성을 가진다.

$step(x)=\begin{cases}1,\quad\text{for }x>0\\0,\quad\text{for }x<0\end{cases}\qquad step'(x)=\begin{cases}0,\quad\text{for }x>0\\0,\quad\text{for }x<0\end{cases}$

def step(x):
    return np.where(x >= 0, 1, 0)
    
def dstep(x):
	return 0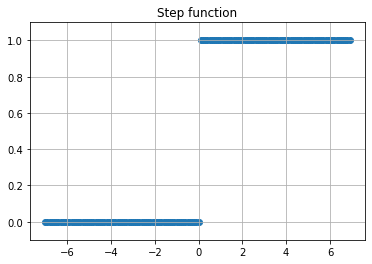

2. Sigmoid function

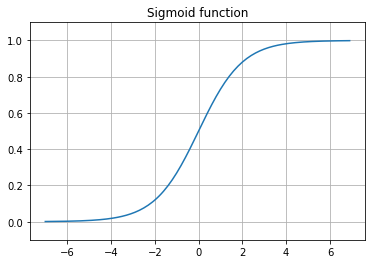
'S모양의'라는 의미를 가진 함수. S자 모양을 가진 함수는 Logistic, Sofmax, Hyperbolic Tangent 같은 함수들이 있다. 앞서 언급한 두 조건을 만족한다. 신경망이 깊어지면 학습이 일어나지 않거나 더뎌진다는 이유로 레이어를 100개 이상 쌓는 요즘은 잘 쓰이지 않고 있다. 다만 분명한 것은 당시에는 퍼셉트론에서 인공신경망으로 한 걸음 나아가게 했던 함수다.

$\sigma(x)=\cfrac{1}{1+e^{-x}}\qquad \sigma'(x)=\cfrac{e^{-x}}{(1+e^{-x})^2}$

def sigmoid(x):
    return 1 / (1 + np.exp(-x))
    
def dsigmoid(x):
	x = np.exp(-x)
    return x / np.square(1 + x)

그래프를 그려보기 전에 3가지 정도 생각해볼 수 있다.

1. $\lim_{x\to +\infty}\sigma(x)=0$
2. $\lim_{x\to0}\sigma(x)=\cfrac{1}{2}$
3. $\lim_{x\to-\infty}\sigma(x)=1$

Step and Sigmoid

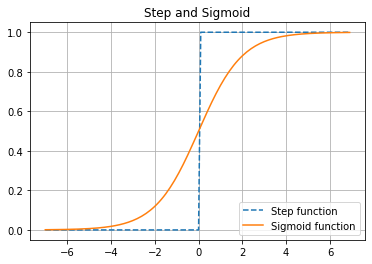
우리가 주목해야 할 것은 두 함수의 출력값인데 계단 함수는 출력값을 0 또는 1외에 다른 값을 가지는 것을 허용하지 않는다. 신경세포도 계단함수처럼 활동한다고 했으니 '신경'망 모델로 활성화 함수에 쓸 수는 있을 것 같은 느낌이 들지만 그렇지 않다. 먼저 특정 값을 경계로 출력값이 양극단으로 몰려있어 입력 레이어에서 전달받은 값을 다음 레이어로 제대로 전해줄 수 없다. $f(x)=1$같은 평행선의 미분값은 0이므로 신경망이 학습을 할 수 없게 한다.

한편 시그모이드 함수는 계단함수와 달리 0에서 1사이의 실수를 출력함수로 가진다. 경계 근처에 있는 값을 허용할뿐만 아니라 가중치를 부여하는 것처럼 정답, 혹은 오답에 가깝게 한다. 그래프도 곡선이라서 미분으로 각 구간별로 기울기를 구할 수 있고 신경망이 학습을 할 수 있게 한다.

Problems of sigmoid

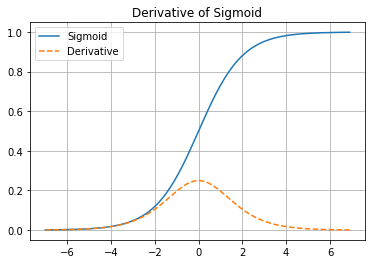
1. Gradient vanishing

Sigmoid function을 미분하면 이렇게 $\sigma(1-\sigma)$ 생겼다. 앞서 구했던 최대값, 최소값, 중간값을 이 식에 대입해보면 양 끝이 0에 가까워지고 중간값이 $\frac{1}{4}$ 을 가진 그래프가 된다. 신경망은 크게 보면 $...\sigma(\sigma(\sigma (\sigma(x))))$의 구조를 가지는데 미분값의 최대값을 이전 레이어로 전달해도 입력층에 다다르면 $\lim_{n\to k}\frac{1}{4}^n$로 소실되는 문제가 있다.

2. Not $0$ centered

$i$번째 weight를 update하는 상황을 수식으로 보자.

$\frac{\partial L}{\partial W_i}$의 부호는 $\frac{\partial L}{\partial f_i}$의 부호에 의존적이다. $x_i$는 $\sigma$의 결과값이므로 항상 양수이기 때문이다. $\frac{\partial L}{\partial f_i}$이 양수일 때 업데이트 방향도 양의 방향으로 반대일 때는 음의 방향으로 업데이트하면서 목표지점까지 바로 못 가고 지그재그로 가게 하는 원인이다. 사실 $\frac{\partial L}{\partial f_i}$은 matrix라서 원소들의 부호는 한가지만 있는 게 아니다. 그래서 1번만큼 심각한 문제는 아니다. 어쨌든 학습은 일어나니까.

3. Computing $e$

Convolution이나 dot product에 비해 연산량이 많지는 않지만 그래도 사칙연산보다 비교적으로 연산량이 많다.

3. Hyperbolic Tangent

기존의 Sigmoid 함수를 좀더 개선했다.

$tanh(x)=\cfrac{2}{1+e^{-2x}}-1\qquad tanh'(x)=\cfrac{4e^{-2x}}{(1+e^{-2x})^2}$

def tanh(x):
    return 2 / (1 + np.exp(-2*x)) - 1
    
def dtanh(x):
	x = np.exp(-2*x)
    return 4 * x / np.square(1 + x)

점화식을 보면 Sigmoid function을 스케일업했다. 위에서 처럼 그래프를 그리기 전에 최대값, 최소값, $f(0)$을 생각해보면 최대값과 최소값은 1과 -1에 각각 접근하고 $f(0)=0$이다.

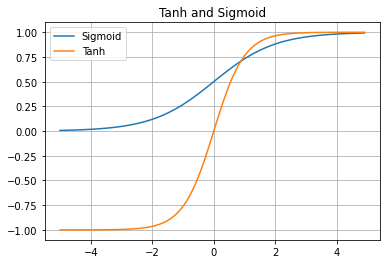
Tanh and Sigmoid

그래프의 중심을 0으로 맞춰서 Sigmoid에서 나타나는 zig-zagging 현상을 해결했지만 여전히 gradient vanishing현상이 나타난다.

4. ReLU

입력값이 0 보다 작으면 0을, 0 이상이면 입력값을 그대로 출력하는 비선형함수다. 앞의 두 함수보다 연산이 효율적이고 학습이 6배 빨라서 요즘 신경망 모델에 널리 사용하고 있다.

$relu(x)=\begin{cases}0,\quad\text{for }x\le0\\ x,\quad\text{for }x\gt0\end{cases}\qquad relu'(x)=\begin{cases}0,\quad\text{for }x\le0\\ 1,\quad\text{for }x\gt0\end{cases}$

def relu(x):
    return np.where(x >= 0, x, 0)
    
def drelu(x):
	return np.where(x >= 0, 1, 0)

식에서 보이듯이 $x>0$일때 기울기가 1인 직선이고 $x<0$일 때 출력값은 언제나 0이다.

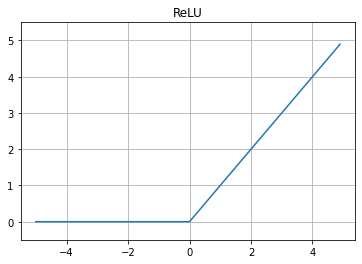
Problems of ReLU

1. Dying ReLU

입력값이 음수일 때 미분값이 0이므로 업데이트가 되지 않는다. 이것을 Dying ReLU라고 하는데 말 그대로 뉴런이 '죽는'현상이 있다. 그래서 bias를 0.01로 초기화 하기도 한다.

2. Gradient exploding

초기 weight가 너무 크거나 learning rate가 너무 높으면 일어난다.

3. Non zero centered

Sigmoid와 같은 문제가 있다.

5. Leaky ReLU

$lrelu(x)=\begin{cases}0.01x,\quad\text{for }x<0\\ x,\quad\text{for }x\ge 0\end{cases}\qquad lrelu'(x)=\begin{cases}0.01,\quad\text{for }x<0\\ 1,\quad\text{for }x\ge 0\end{cases}$

def lrelu(x):
    return np.where(x >= 0, x, 0.01*x)
    
def dlrelu(x):
	return np.where(x >= 0, 1, 0.01)

$x<0$일 때 미분값이 0이 아니라서 dying relu를 해결했다는 점을 빼면 Relu와 성질이 같다.

Epilogue

이것 말고도 활성화 함수는 많이 있다.

1. 웬만하면 Sigmoid와 Tanh는 피할 것.
2. ReLU를 가장 먼저 시도해볼 것.
3. 각 함수를 미분한 최대값, 최소값을 구해서 어떤 문제가 있는지 생각해볼 것.

이번 글을 쓰면서 수학공부를 더 해야겠다고 다시 한 번 느꼈다. 수식을 기하학으로 연결하는 감각도 필요한 것 같다.