Prologue
인공신경망 학습기법에 관한 연구가 활발해지면서 학습속도를 개선하고 100개 넘는 레이어를 쌓는 일도 쉽게 할 수 있게 되었다. 가중치를 어떻게 초기화하냐에 따라 gradient vanishing/exploding을 막으면서 학습을 진행할 수 있다.
AlexNet에서
그랬던 것처럼 평균이 0, 분산을 0.01으로 가중치를 초기화를 하고 레이어를 5보다 좀더 늘려서 한 번만 돌려보자.
dims = [4096] * 10
tanh = []
x = np.random.randn(16, dims[0])
for Din, Dout in zip(dims[:-1], dims[0:]):
W = 0.01 * np.random.randn(Din, Dout)
x = np.tanh(x.dot(W))
tanh.append(x)
plt.figure(figsize = (15, 3))
for i, H in enumerate(tanh):
plt.subplot(1, len(tanh), i+1)
plt.hist(H.ravel(), 40, (-1, 1))
if i != 0 : plt.yticks([],[])
plt.xlabel('layer ' + str(i + 1))
plt.suptitle('Tanh with AlexNet initialization')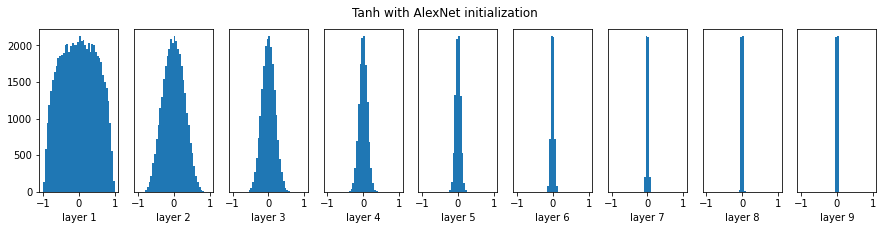
풍성하던 데이터분포가 평균 근처로 쪼그라들었다. tanh는 너무 크거나 너무 작은 값은 1과 -1에 가까운 값으로 수렴하기 때문이다.
Scale up
그래서 간단히 입력값을 스케일업하면 되지 않을까하는 아이디어에서 다시 실험을 진행해봤다.
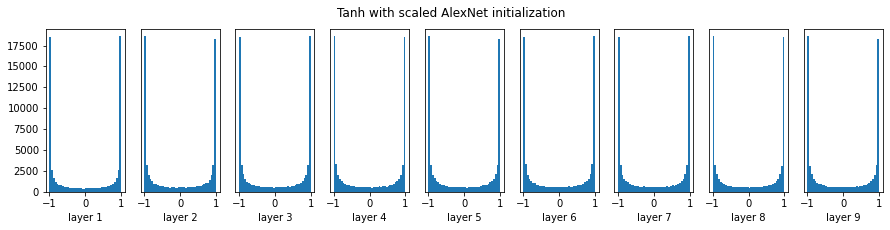
오막깟! 이러면 지난 글에서 봤듯이 가중치 초기값이 크면 일어나는 문제가 생긴다 activation function이 S자 모양이면 gradient vanishing이 학습을 방해하고, relu계열이면 gradient exploding때문에 모델이 학습을 할 수가 없다. 학습률을 낮춰서 어떻게든 되게 한다고 하더라도 학습이 느리다. 우리 시간은 한정되어 있고 그렇게 많지 않다.
Xavier initialization
복잡한 문제는 직관적으로 풀면 오히려 쉽게 풀릴 때가 있다. 레이어 중간을 똑 떼와서 라고 할 때 의 분산을 이라고 하자.
cs213n에서는 일반적으로 weight의 분산은 입력값의 갯수가 많아지면 함께 커진다는 점이 안정적인 학습을 막는다고 하고 있다.
우리가 하고 싶은 건 의 분산을 일정하게 유지하는 건데 간단히 의 분산이 이라면 의 분산을 첫번째 레이어부터 마지막 레이어까지 1로 고정할 수 있을 거다. 그러면 0.01 대신에 을 곱하면 잘 되지 않을까? 하는 직관이 논문에 녹아있고 cs231n에서 이렇게 증명하고 있는데 3번째 줄이 왜 그런지 지금은 잘 이해가 안 된다(는 여기에서 그렇게 된다고 증명했다).
scaled = []
for Din, Dout in zip(dims[:-1], dims[1:]):
Ws = np.sqrt(1/Din)* np.random.randn(Din, Dout)
x = np.tanh(x.dot(Ws))
scaled.append(x)
plt.figure(figsize = (15, 3))
for i, H1 in enumerate(scaled):
plt.subplot(1, len(scaled), i+1)
plt.hist(H1.ravel(), 40, (-1, 1))
if i != 0 : plt.yticks([],[])
plt.xlabel('layer ' + str(i + 1))
plt.suptitle('Tanh with Xavier initialization')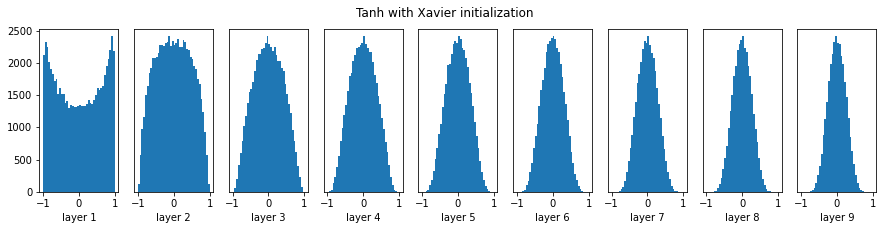
오! 아까보다 훨씬 좋다. 그러면 relu에서도 잘 될까?
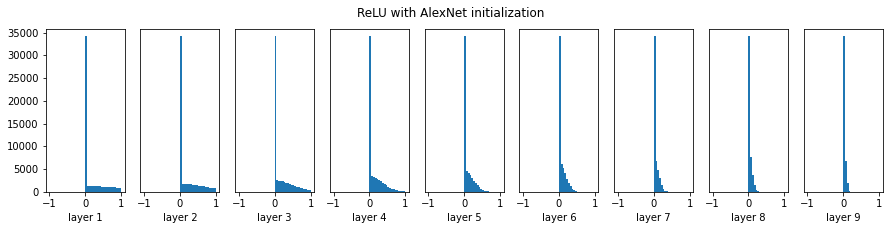
...잘 안된다. 음수는 싹 없어지고 뒤에 있던 꼬리마저 짧아진다. Xavier initialization으로 S자 함수는 잘 쓸 수 있게 됐지만 relu를 쓰려면 실험을 많이 해야 했을 거다.
He initialization
relu layer를 지나면서 원본 데이터의 절반을 잃어버리는 샘인데 그래서 분산을 Xavier initialization에서 2배 늘려보기로 한다.
he = []
x = np.random.randn(16, dims[0])
for Din, Dout in zip(dims[:-1], dims[1:]):
Wm = np.random.randn(Din, Dout) * np.sqrt(2/Din)
x = np.maximum(0, x.dot(Wm))
he.append(x)
plt.figure(figsize = (15, 3))
for i, H in enumerate(he):
plt.subplot(1, len(he), i+1)
plt.hist(H.ravel(), 40, (-1, 1))
if i != 0 : plt.yticks([],[])
plt.xlabel('layer ' + str(i + 1))
plt.suptitle('ReLU with He initialization')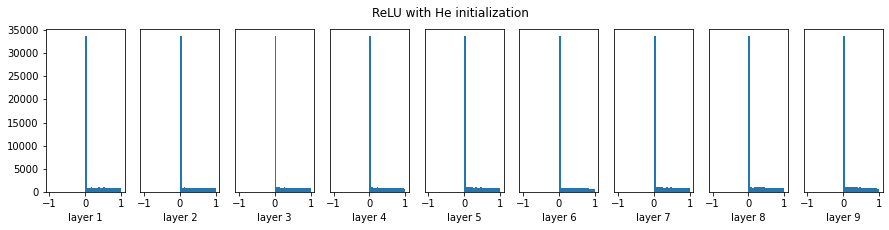
여전히 데이터의 절반은 없어지지만 양수 부분은 잘 가지고 있다.
Epilogue
학습을 잘 하기 위한 가중치 초기화 기법을 짚어봤다. 가중치 초기화를 하면 무조건 학습이 더 잘 된다고 하기는 어렵다. 레이어를 많이 쌓으면 데이터분포가 다시 쪼그라들 거라고 짐작할 수 있다. 이것이 Batch normalization 연구의 배경 중 일부지만 최근들어 Batch normalization이 잘 되는 이유에 대해서는 의견이 분분하다. 구체적인 내용은 다음에 알아보자.