Prologue

열역학에서 많이 쓰이지만 Claude Shannon의 정보이론에서는 정보량을 효율적으로 계량하는데 쓰인다. 결론부터 말하면 entropy는 자주 등장하지 않는 정보일수록, 그러니까 일어날 확률이 낮은 사건일수록 커진다.

Amount of Information

두 가지 예를 들어보자.

1. 개가 사람을 물 확률: $99\%$
2. 사람이 개를 물 확률: $1\%$

두 사건이 일어날 때마다 어디론가 정보를 보내야 할 때 같은 정보량으로 보내보자. 이를테면 0.1 같은 작은 수로 정하고 사건이 100번이 일어났다고 했을 때 총 정보량은 $10$이다.$(9.9 + 0.1)$ 여기에서 정보량을 좀더 줄일 수 있는 방법이 있나? 하고 생각해보면 사건이 일어날 확률을 그냥 뒤집어서 사용하는 거다.

1. 개가 사람을 물 확률의 정보량: $\frac{1}{99}$
2. 사람이 개를 물 확률의 정보량: $1$

이렇게 100번이 일어났다고 했을 때 총 정보량은 $2$로 확 줄어든다.$(99\cdot\frac{1}{99} + 1)$

이런 관점에서 entropy 점화식을 뜯어보자.

서로 다른 사건이 일어날 확률을 계산할 때는 각 사건이 일어날 확률을 곱셈으로 계산하고 이렇게 구한 확률들을 더해준다는 점을 알 수 있는데 정보량을 곱셈과 덧셈으로 계산하게 하는 방법이 $\log$다.

그러면 확률이 다른 사건을 다뤄보자. 서로 독립인 두 사건의 확률이 각각 $0.32$, $0.64$일 때 두 사건이 동시에 일어날 확률을 한 번 계산해보자.

곱과 합이 모두 보인다. 이 결과를 $\log$로 바꿔서 역수로 만들어 주면 두 사건의 정보량을 잴 수있는 모양으로 바뀐다.

Think visually

좀 더 쉽게는 최소 저장단위는 0, 1로 표현하는 bit다. 그래서 밑을 2로 하는 $\log$그래프를 그려준다.

$f(x)=\log_2{x}$

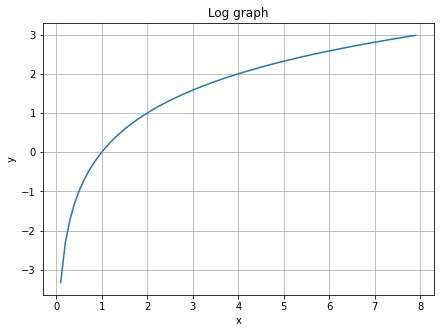
확률의 범위는 $[0,\ 1]$이므로 그래프의 범위를 좁혀준다. 참고로 정보이론에서는 $0\log0=0$으로 정의한다.

$f(x)=\log_2{x},\quad\text{where }0\le{x}\le{1}$

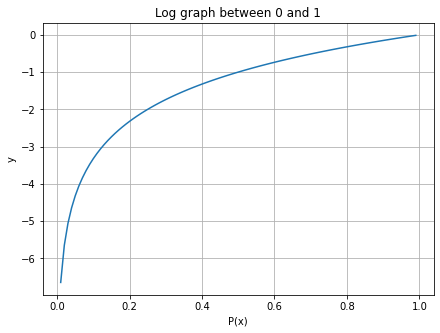
상식적으로 "컵에 물이 $-200ml$가 있다."라는 문장이 말이 안 되듯, 정보량 또한 $(0,\ \infty]$이므로 이 그래프를 뒤집어준다.

$f(x)=-\log_2{x},\quad\text{where }0\le{x}\le{1}$

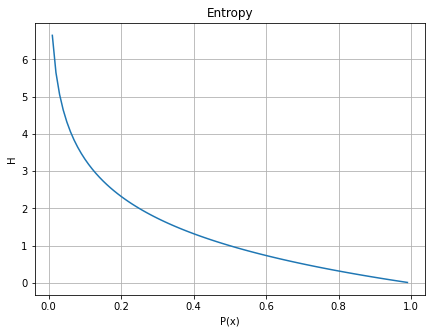
그래프를 딱 보면 어떤 사건이 일어날 확률이 낮을 수록 정보량이 크고 높을수록 정보량이 낮다는 것을 알 수 있다.

Epilogue

그러면 한 걸음 더 나아가서 언제 entropy가 높은지 생각해보자. 3가지 종류의 동전을 2번 던진다고 해보자.

1. 앞, 뒤가 나올 확률이 같은 동전
   $-\log_2{0.5}\cdot0.5\cdot2 = 2$
2. 앞이 나올 확률이 0.7, 뒤가 나올 확률이 0.3인 동전
   $-\log_2{0.7}\cdot0.7 - \log_2{0.3}\cdot0.3 = 0.881$
3. 앞이 나올 확률이 0.9, 뒤가 나올 확률이 0.1인 동전
   $-\log_2{0.9}\cdot0.9 - \log_2{0.1}\cdot0.1 = 0.468$

모든 사건이 일어날 확률이 같을 때 entorpy가 가장 높다. 이것도 썩 자연스럽다. 1번 동전을 다시 던질 때 앞면이 나올지 뒷면이 나올지 확실하게 말할 수 없지만 2번이나 3번동전을 던진다면 1번 동전에 비해 2번 동전이, 2번 동전에 비해 3번동전이 앞면이 나온다고 확실하게 말할 수 있다. 이런 측면에서 봤을 때도 entropy가 불확실성을 계량한다는 말도 된다.