Prologue

아이유 말고 아이오유. Object detection 모델 논문을 보면 AP50이나 AP75처럼 AP(Average Precision)에 옵션을 달아두는 식으로 자주 만날 수 있다. 논문 읽을 때는 소화하기에 급급해서 느낌적 느낌으로 '아, 그렇구나'하고 넘어갔다. 이번 기회에 정리를 해둬야겠다고 마음먹었다.

It's one of eveluation metrics

Intersection of union를 이렇게 줄여서 쓴다. Pascal VOC, MSCOCO 등의 데이터셋에서 모델을 평가하는 데 쓰인다. 일반적으로 분류나 회귀과제에서 MAE나 MSE를 평가지표로 삼는 반면 object detection이나 segmentation의 경우 평가하기가 애매해서 통계학으로부터 자카드 지수라는 통계값을 가져왔다.

$J(\text{A, B})=\begin{array}{c}\text{A}\cap\text{B}\\\hline\text{A}\cup\text{B}\end{array}$

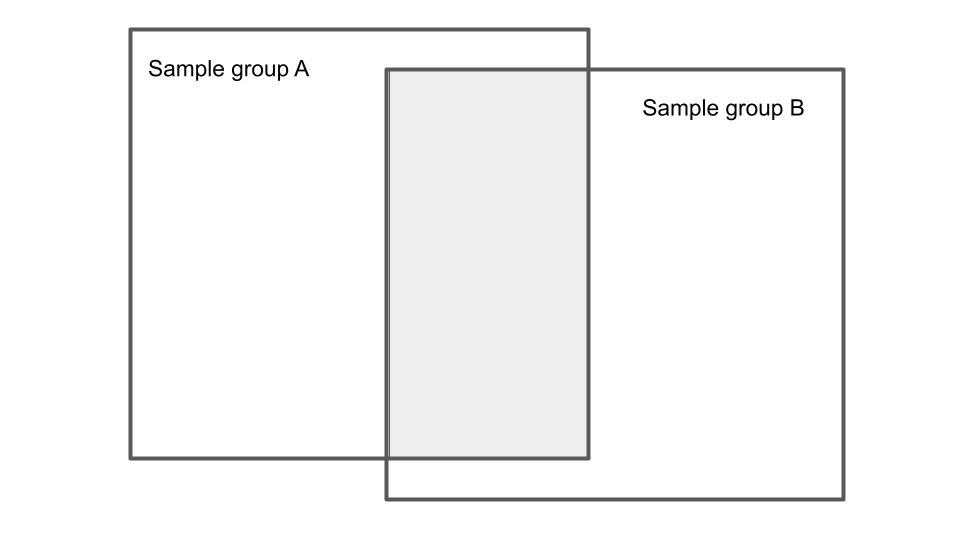
원래 자카드 지수는 두 표본집단이 얼마나 비슷한지 알아보는데 쓴다. 두 표본집단의 합집합을 1로 했을 때 교집합의 비율인데 0과 1사이의 값을 가지고 1에 가까울 수록 두 표본집단이 비슷다하고 말할 수 있다.

IoU는 이 아이디어를 가져왔다. 목표 object의 정답 bounding box(bbox)와 모델이 예측하는 bbox가 얼마나 비슷한지 자카드 지수로 평가한다. 과제마다 다르겠지만 일반적으로 0.5가 넘으면 잘 잡아냈다고 보고 threshold의 기준으로 삼곤 한다.

$\text{IoU}=\begin{array}{c}\text{Area of Intersection}\\\hline\text{Area of Union}\end{array}$

Time to implement

IoU의 개념을 알아봤다. 이제는 구현할 차례. IoU를 구하는데는 각 bbox의 두 좌표만 알면 된다. 왼쪽 상단, 오른쪽 하단. 혹은 그 반대가 되도 상관없다. 좌표평면상의 원점은 왼쪽 하단이지만 컴퓨터 입장는 이미지의 왼쪽 상단을 원점으로 생각한다. 여기서는 쉽게 편의상 좌표평면을 빌려올 거다.

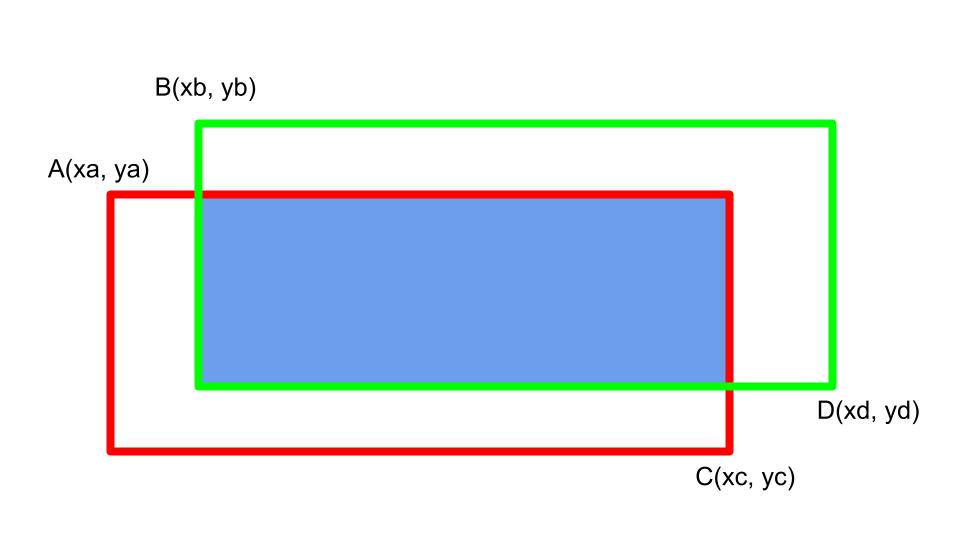
우리가 알고 싶은 것은 두 bbox가 겹치는 영역이다. 위 이미지에서 정답 bbox를 빨간색, 모델이 예측한 bbox를 초록색이라고 하자. 그리고 각 bbox의 왼쪽 상단, 오른족 하단 좌표를 알고 있다고 할 때 두 bbox가 겹치는 영역의 두 좌표를 알면 넓이를 구할 수 있다.

복잡해보이지만 각 좌표들을 크기순으로 나열했을 때 중간에 있는 좌표값들을 구하면 겹치는 영역의 좌표를 구할 수 있다.

$x_a<x_b<x_c<x_d$
$y_c<y_d<y_a<y_b$

정리해보면 왼쪽 상단 좌표 x값 중 큰 값, y값 중 작은 값을 선택해서 $(x_b,\ y_a)$, 오른쪽 하단 좌표는 x값 중 작은 값, y값 중 큰 값을 선택해서 $(x_c, \ y_d)$가 되겠다.

def get_iou(bbox_gt: list, bbox_p: list) -> float:
    '''
    Args
    	bbox_gt: List of ground truth coordinate.
        [upper left x, upper left y, bottom right x, bottom right y]
    	bbox_p: List of predicted coordinate.
        [upper left x, upper left y, bottom right x, bottom right y]
    return
    	Float Ratio of 2 bbox is overlapped
    '''
    x1 = max(bbox_gt[0], bbox_p[0])
    y1 = min(bbox_gt[1], bbox_p[1])
    x2 = min(bbox_gt[2], bbox_p[2])
    y2 = max(bbox_gt[3], bbox_p[3])
    
    intersection = (x2 - x1) * (y1 - y2)
    
    gt = (bbox_gt[2] - bbox_gt[0]) * (bbox_gt[1] - bbox_gt[3])
    p = (bbox_p[2] - bbox_p[0]) * (bbox_p[1] - bbox_p[3])
    
    union = gt + p - intersection
    
    iou = intersection / union
    
    return iou
    
bbox_gt = [250, 480, 580, 300]
bbox_p = [260, 500, 500, 320]
get_iou(bbox_gt, bbox_p)

>>> 0.5981308411214953

Epilogue

이 글로 IoU를 알았다. 앞으로 논문을 좀더 잘 이해할 수 있게 됐고 mAP를 이해할 준비가 됐다. 동시에 모델이 어떻게 bbox를 예측하는지 궁금해졌다고 생각한다. 그건 다른 글에서 알아보기로 하자.