Prologue

Gradient descent가 발전해온 방향은 크게 두 가지가 있다. 첫 번째는 물리법칙을 따르는 방법, 두 번째는 학습을 거듭할수록 일정비율로 학습률을 줄여서 global minima를 지나가지 않게 하는 방법이 그것이다. 이번에는 일정비율로 학습률을 줄이는 방법을 알아볼 거다.

import numpy as np
import matplotlib.pyplot as plt

def f(x, y):
    return 0.4*x**2*y**2 + 0.3*x**2*y + 0.3*x**2 + 0.3*y**2 - 0.25*x*y**2 + 0.31*x*y - 0.2*x + 2.1*y

def df(x, y):
    dx = 0.8*x*y**2 + 0.6*y + 0.6*x - 0.5*y + 0.31*y - 0.2
    dy = 0.8*x**2*y + 0.6*x**2 + 0.6*y - 0.5*x*y + 0.31*x + 2.1
    return dx, dy

x = np.arange(-1, 2, 0.01)
y = np.arange(-2, 1, 0.01)
X, Y = np.meshgrid(x, f(x, y))
Z = np.sqrt(X**2 + Y**2)
plt.contour(X, Y, Z, 25, colors = ['gray'])
plt.plot(x, f(x, y))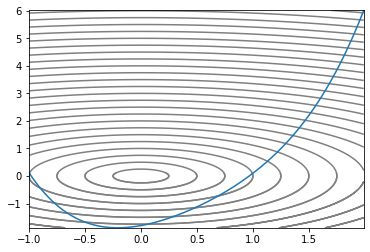

우리가 헤멜 Convex 지형이다. 2차원의 2차함수에다 z축을 하나 추가해서 입체적으로 만들고 등고선처럼 높이가 같은 지점끼리 선으로 이었다. 가장 작은 원이 최소값을 갖는 지점이므로 optimizer가 저 원을 콕 찍으면 된다.

Adagrad

"적응하는 경사하강법"

학습을 거듭하면 모델이 놓이는 환경이 달라지는데 학습률이 변하지 않으면 global minima를 휙 지나칠 수도 있으니까 학습을 거듭할 수록 학습률을 낮추면 어떨까? 하는 아이디어에서 출발했다. 이전의 알고리즘은 모든 parameter에 같은 학습율로 업데이트했다면 adagrad는 모든 parameter에 각각 다른 학습률로 업데이트한다. 업데이트 규칙을 간단히 말하면 학습을 거듭할수록 parameter가 변할텐데 변화가 클수록 작게, 작을 수록 변화를 많이 주겠다는 거다. 점화식을 뜯어보자.

$h_n = h_{n-1}+\nabla f(\theta_n)\odot \nabla f(\theta_n), \ h_1=0$
$\theta_{n+1}=\theta_n-\alpha\cfrac{1}{ \sqrt{h_n}}\nabla f(\theta_n)$

학습률 계산하는 부분을 빼면 일반적인 경사하강법과 크게 차이가 없다. 이때 눈여겨 봐야할 점이 있는데 $h_n$에는 gradient의 제곱이 누적하는데 좀 넓게 보자면

$h_n = \sum_{k=0}^n \nabla f(\theta_k)\odot\nabla f(\theta_k)$

이렇게도 볼 수 있다. 이것이 썩 자연스러운 이유가 두 가지가 있다.
1. 학습 후반으로 갈수록 $h_n$은 점점 커져서 학습률은 자연스럽게 작아진다.
2. 또 gradient 행렬의 관점에서 변화량이 클수록 제곱하면 큰 값이 쌓이고 작을 수록 작은 값이 쌓여서 역수에 루트를 씌워주면 변화량이 큰 값은 학습률의 변화를 작게, 변화량이 작은 값은 학습률의 변화를 크게 한다.

def adagrad(x, y, cache: dict, lr = 5e-1):
    dx, dy = df(x, y)
    if len(cache['x']) == 0:
        hx = np.square(dx)
        hy = np.square(dy)
    else:
        hx = cache['x'][-1] + np.square(dx)
        hy = cache['y'][-1] + np.square(dy)
    cache['x'].append(hx)
    cache['y'].append(hy)
    x = x - lr * dx/(np.sqrt(hx) - 1e-8)
    y = y - lr * dy/(np.sqrt(hy) - 1e-8)
    return x, y

cache = {'x':[], 'y':[]}
adaX, adaY = [.5], [5.8]
x, y = adagrad(*adaX, *adaY, cache)
adaX.append(x)
adaY.append(y)
for i in range(60):
    x, y = adagrad(x, y, cache)
    adaX.append(x)
    adaY.append(y)
    
plt.contour(X, Y, Z, 25, colors= ['gray'])
plt.plot(adaX, adaY)
plt.title('Adagrad')
plt.xlabel('lr=5e-1, epochs=60')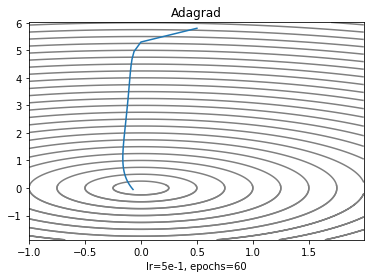

RMSProp

Adagrad와 비슷한 알고리즘인데 특이하게 논문이 없다. Geroffery Hinton 교수님이 코세라 강의에서 "이렇게 하면 더 잘 되던데?" 하면서 소개했고 논문이 없으니까 후에 연구자들이 Reference에다가 강의제목을 넣기도 했다. 앞서 살펴본 Adagrad는 학습 후반으로 갈수록 학습률이 낮아져서 더이상 metric이 개선되지 않는 지점이 온다는 문제가 있다. 이것을 보완하려고 RMSProp은 누적 gradient와 현재 gradient의 비율을 조절하기로 한다.

$h_n = \gamma h_{n-1}+(1-\gamma)\nabla f(\theta_n)\odot \nabla f(\theta_n), \ \ h_1=0$
$\theta_{n+1}=\theta_n-\alpha \nabla f(\theta_n) \cfrac{1}{\sqrt{h_n}+\epsilon}$

$\gamma$는 decay rate라고 하고 현재의 누적값과 과거의 누적값의 비율을 조절한다.

def rmsprop(x, y, cache: dict, gamma = 0.9, lr = 5e-2):
    dx, dy = df(x, y)
    if len(cache['x']) == 0:
        hx = (1-gamma) * np.square(dx)
        hy = (1-gamma) * np.square(dy)
    else:
        hx = gamma * cache['x'][-1] + (1-gamma) * np.square(dx)
        hy = gamma * cache['y'][-1] + (1-gamma) *  np.square(dy)
    cache['x'].append(hx)
    cache['y'].append(hy)
    x = x - lr * dx/(np.sqrt(hx) + 1e-8)
    y = y - lr * dy/(np.sqrt(hy) + 1e-8)
    return x, y

cache = {'x':[], 'y':[]}
rmspX, rmspY = [.5], [5.8]
x, y = rmsprop(*rmspX, *rmspY, cache)
rmspX.append(x)
rmspY.append(y)
for i in range(60):
    x, y = adagrad(x, y, cache)
    rmspX.append(x)
    rmspY.append(y)
    
plt.contour(X, Y, Z, 25, colors= ['gray'])
plt.plot(rmspX, rmspY)
plt.title('RMSProp')
plt.xlabel('gamma=0.9, lr=1e-3, epochs=60')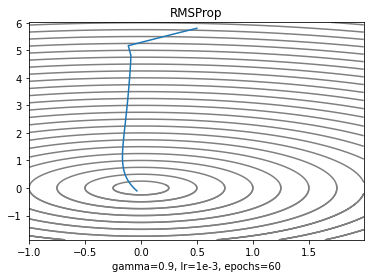

Epilogue

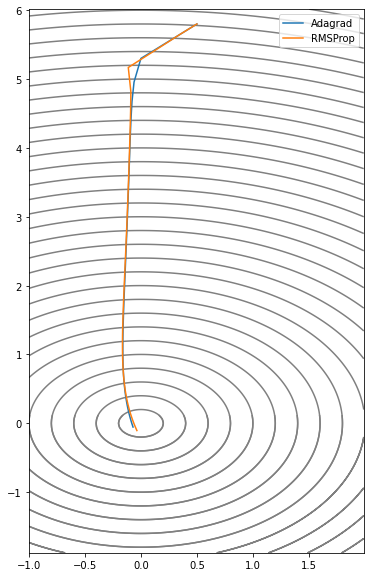
그래프 상으로 별차이가 없어보이지만 RMSProp이 $\gamma$값을 조절할 수 있어서 숨통이 트인다. $\gamma$값을 0.9로 하면 이 과제에서 60 epoch에 수렴한다. 아무래도 학습하면서 학습률을 낮춰서 그런가 Momentum 계열의 optimizer에 비해 높은 학습률을 요구하는 것 같다.