Prologue

Gradient descent가 발전해온 방향은 크게 두 가지가 있다. 첫 번째는 물리법칙을 따르는 방법, 두 번째는 학습을 거듭할수록 일정비율로 학습률을 줄여서 global minima를 지나가지 않게 하는 방법이 그것이다. 이번에는 물리법칙을 따르는 방법을 알아볼 거다.

import numpy as np
import matplotlib.pyplot as plt

def f(x, y):
    return 0.4*x**2*y**2 + 0.3*x**2*y + 0.3*x**2 + 0.3*y**2 - 0.25*x*y**2 + 0.31*x*y - 0.2*x + 2.1*y

def df(x, y):
    dx = 0.8*x*y**2 + 0.6*y + 0.6*x - 0.5*y + 0.31*y - 0.2
    dy = 0.8*x**2*y + 0.6*x**2 + 0.6*y - 0.5*x*y + 0.31*x + 2.1
    return dx, dy

x = np.arange(-1, 2, 0.01)
y = np.arange(-2, 1, 0.01)
X, Y = np.meshgrid(x, f(x, y))
Z = np.sqrt(X**2 + Y**2)
plt.contour(X, Y, Z, 25, colors = ['gray'])
plt.plot(x, f(x, y))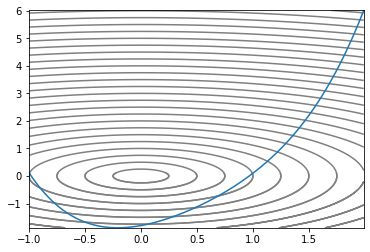

우리가 헤멜 Convex 지형이다. 2차원 2차함수에다 z축을 하나 추가해서 입체적으로 만들고 등고선처럼 높이가 같은 지점끼리 선으로 이었다. 가장 작은 원이 최소값을 갖는 지점이므로 optimizer가 저 원을 콕 찍으면 된다.

SGD

최적화 기법중에서 가장 간단해서 많은 예시와 논문에서 볼 수 있다. gradient를 기반으로 움직이는 거리가 정해지므로 산 중턱에서 바퀴를 굴릴 때 바퀴에 미치는 영향은 중력만 있는 샘이다.

$\theta_n = \theta_{n-1} - \alpha \nabla f(\theta_{n-1})$

def sgd(x, y, lr = 1e-2):
    dx, dy = df(x, y)
    x -= lr * dx
    y -= lr * dy
    return x, y
    
sgdX, sgdY = [.5], [5.8]
x, y = sgd(*sgdX, *sgdY)
sgdX.append(x)
sgdY.append(y)
for i in range(160):
    x, y = sgd(x, y)
    sgdX.append(x)
    sgdY.append(y)
    
plt.contour(X, Y, Z, 25, colors = ['gray'])
plt.plot(sgdX, sgdY)
plt.title('SGD')
plt.xlabel('lr=1e-2, epochs=160')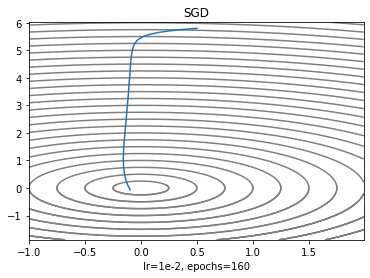

Momentum

SGD는 gradient가 0이 되면 더이상 업데이트를 하지 않으므로 local minima, plataeu, saddle point에서 벗어나기 힘들다. 그런데 관성이 충분히 크면 턱을 넘을 수 있을 거라는 아이디어에서 출발했다.

$v_{n+1} = \mu v_{n} - \alpha \nabla J(\theta_{n}), \ \ v_1=0$
$\theta_{n+1} = \theta_{n} + v_{n}$

시작점에서 관성이 0이라는 점은 감각적으로 알 수 있다. $\mu$는 momentum coefficient라고 해서 일종의 마찰이라고 생각하면 된다. 우리 바퀴는 우주공간으로 가지 않는 이상 공기저항으로부터 벗어날 수없으므로 0.5, 0.9, 0.95, 0.99 이런 식으로 바꾸면서 학습이 잘 되는 지점을 찾는다.

def momentum(x, y, cache: dict, rho = 0.9, lr=5e-3):
    dx, dy = df(x, y)
    if len(cache['x']) == 0:
        vx = -lr * dx
        vy = -lr * dy
    else:
        vx = rho * cache['x'][-1] - lr * dx
        vy = rho * cache['y'][-1] - lr * dy    
    cache['x'].append(vx)
    cache['y'].append(vy)
    x = x + vx
    y = y + vy
    return x, y

cache = {'x':[], 'y':[]}
mmtX, mmtY = [.5], [5.8]
x, y = momentum(*mmtX, *mmtY, cache)
mmtX.append(x)
mmtY.append(y)
for i in range(32):
    x, y = momentum(x, y, cache)
    mmtX.append(x)
    mmtY.append(y)
    
plt.contour(X, Y, Z, 25, colors= ['gray'])
plt.plot(mmtX, mmtY)
plt.title('Momentum')
plt.xlabel('momentum=0.9, lr=5e-3, epochs=32')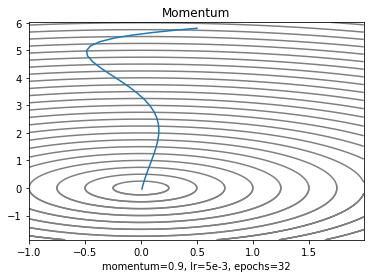

Nesterov Accelerateing Gradient descent

Momentum의 개량형이다. 관성을 가진 바퀴가 눈도 달렸다. 이제는 경사를 보고나서 더 빠르게 내려가는 방향으로 내려갈 거다.

$v_n = \rho v_{n-1} + \alpha\nabla J(\theta_n-\rho v_{n-1}), \ \ v_1=0$
$\theta_{n+1} = \theta_n - v_n$

Momentum은 일단 gradient의 반대방향으로 간 다음에 무조건 과거의 운동량에 비례해서 더 가는 반면에 NAG는 과거의 운동량만큼 가서 gradient를 계산하고 움직인다는 점이 가장 큰 차이점이다.

def nesterov(x, y, cache: dict, gamma = 0.9, lr = 5e-3):
    if len(cache['x']) == 0:
        dx, dy = df(x, y)
        vx = lr * dx
        vy = lr * dy
    else:
        dx, dy = df(x - gamma * cache['x'][-1], y - gamma * cache['y'][-1])
        vx = gamma * cache['x'][-1] + lr * dx
        vy = gamma * cache['y'][-1] + lr * dy
    cache['x'].append(vx)
    cache['y'].append(vy)
    x = x - vx
    y = y - vy
    return x, y

cache = {'x':[], 'y':[]}
nestX, nestY = [.5], [5.8]
x, y = nesterov(*nestX, *nestY, cache, 0.9)
nestX.append(x)
nestY.append(y)
for i in range(34):
    x, y  = nesterov(x, y, cache)
    nestX.append(x)
    nestY.append(y)
    
plt.contour(X, Y, Z, 25, colors= ['gray'])
plt.plot(nestX, nestY)
plt.title('Nestrov')
plt.xlabel('$\gamma=0.95$, lr=5e-3, epochs=34')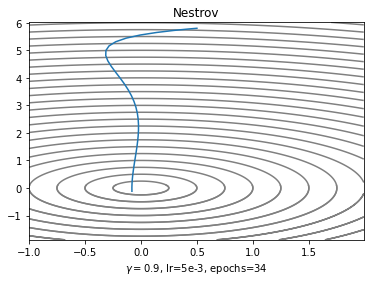

Epilogue

plt.figure(figsize = (6, 10))
plt.contour(X, Y, Z, 40, colors= ['gray'])
plt.plot(sgdX, sgdY, label = 'SGD')
plt.plot(mmtX, mmtY, label = 'Momentum')
plt.plot(nestX, nestY, label = 'Nesterov')
plt.legend()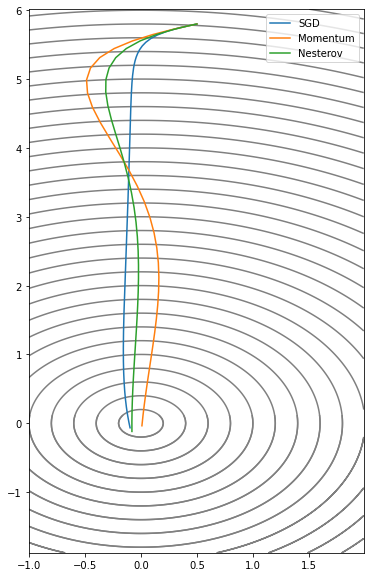

Momentum과 Nesterov의 공통점은 학습 초기에 loss의 최소값이라고 생각하는 방향으로 일단 한 걸음 크게 내딪는다는 점이다(over shooting). 그 후에 방향이 변한다면 변한 방향으로 크게 한 걸음 내딪는다는 특징이 있다. 사실 점화식으로 봐서는 Momentum이나 Nesterov나 계산하는 순서말고 차이를 잘 모르겠지만 실제로 써보면 loss가 진동하는 과제에서는 Nesterov가 성능이 더 좋다고 한다.