Prologue

CNN을 공부하다 보면 FCN, FPN 처럼 conv layer로 줄어든 spatial dimension을 다시 키우는 network와 마주한다.

FCN

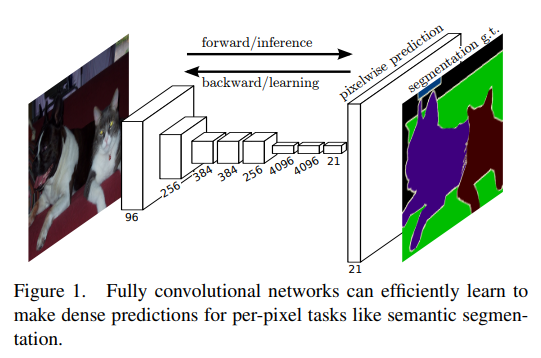
FPN

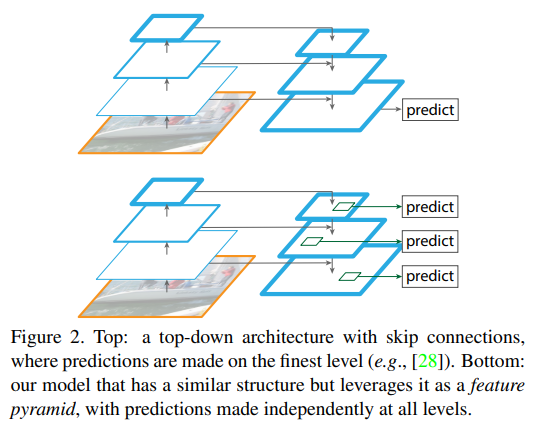
이 과정을 지칭하는 용어도 upsampling, unpooling, deconvolution, transeposed convolution이 있는데 여러 연구에서 하나로 딱 쓰고 있지 않아서 더욱 헷깔리게 한다.

Upsampling

엄밀히 말하면 작아진 spatial demension을 크게 한다고 해서 최상위 개념은 upsampling이다. 그 하위 개념으로 unpooling, deconvolution 이 있다.

Unpooling

max pooling의 반대. max pooling은 kernel 안에 있는 신호 중 가장 높은 값만을 남겨서 노이즈를 제거하고 연산량을 줄인다. classification하는데는 좋은 성능을 보이지만 물체의 정확한 위치를 알아야 하는 과제에서는 오히려 average pooling이 더 좋다고 알려져있다.

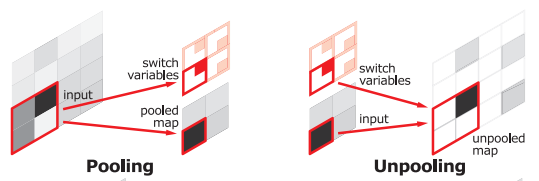
pooling을 하면서 최댓값의 위치를 기억해뒀다가 unpooling할 때 제자리로 돌려놓고 빈 공간은 최댓값으로 채우면서 spatial demension을 원래 크기로 돌려놓는다. 다른 말로 unlearnable upsampling이라고 한다.

Deconvolution

용어부터 바로 잡자. 어떤 연구에서는 tensor를 convolution 하기 전으로 돌려놓는다고 해서 deconvolution이라고 쓰는 것 같다. cs231n에서는 엄밀히 따지면 수학에서 말하는 deconvolution과는 연산이 달라서 transposed convolution이라고 부르는 게 바람직하다고 짚고 있고 tensorflow에서도 Conv2DTranspose라는 이름으로 구현하고 있다.

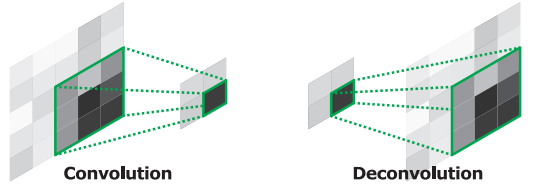
$\small\text{Figure 1}$에서 나와있다시피 transposed convolution은 backward pass에서 학습이 일어난다. 이게 unpooling과의 가장 큰 차이점이다. 그러면 왜 transposed convolution인지 알아보자.

im2col

입력 tensor와 kerenl을 각각 $X$, $W$로 하는 conv layer를 아래와 같이 정의할 수 있다. 편의를 위해 padding=0, strides=1로 한다.

이 연산의 결과는 $X\circledast W\in\mathbb{R}^{2\times2}$라고 쉽게 알 수 있다. 다시 한 번 말하지만 이건 연산량이 $O(n^4)$ 만큼 들어서 $X$와 $W$의 모양을 한 번 바꿔서 연산한다.

그러면 결과 vector $r$은 $\mathbb{R}^{1\times4}$에 속하고 다시 $\mathbb{R}^{2\times2}$에 속하는 $R$로 다시 정렬해서 쓴다.

Transposed convolution

conv layer에 의해 줄어든 tensor를 다시 원래 크기로 돌리는 방법은 im2col과 크게 다르지 않다. 간단하다.

문제를 이렇게 정의할 때 입력 vector $x^T$와 같은 모양을 같게하는 모양을 찾으면 $W_2$는 $\mathbb{R}^{4\times9}$에 속하는 matrix다. 여기에서 왜 transposed convolution이라고 부르는지 드러나는데 $W_2$의 모양은 $W_1^T$의 모양과 일치해서 transposed convolution이라고 부른다. 그래서 deconvolution보다는 transposed convolution이라고 부르는 편이 더 직관적이다.

Epilogue

transposed convolution도 conv layer처럼 연산하는 방법이 따로 있는데 이것도 한 번 알아봐야겠다.