
해시 테이블 (Hash Table)
해시 테이블 (Hash Table) 을 사용하면 자료를 쉽고 빠르게 저장할 수 있고, key - value 쌍 기반의 자료를 얻을 수 있어요. 자바스크립트의 내장 객체가 동작하는 방식과 같죠.

해시 테이블에서는 put() 과 get() 이라는 두 가지 주요 함수가 있어요. put()은 해시 테이블에 자료를 저장할 때 사용되고, get()은 반대로 해시 테이블의 정보를 얻어낼 때 사용되죠. 두 함수는 모두 시간 복잡도가 O(1)이에요.
간단히 말해서 해시 테이블은 인덱스가 해싱 함수에 의해 계산되는 배열과 유사해요. 이 때 인덱스는 메모리에서 유일한 공간을 식별하기 위한 것이죠. localStorage가 바로 이 해시 테이블에 기반한 자료 구조의 대표적인 예에요.
해싱 (Hashing)
해시 테이블에서 가장 중요한 부분은 해시 함수 에요. 해시 함수는 특정 키를 자료를 저장하는 배열의 인덱스로 변환하죠.
좋은 해시 함수의 주요 요구 사항
결정성: 동일한 키는 동일한 해시 값을 생성해야 한다ㅏ.
효율성: 시간 복잡도가 O(1)이어야 한다.
균일한 분배: 배열 전체를 최대한 활용해야 한다.
소수 해싱
해싱에서 소수 는 매우 중요해요. 소수를 사용한 모듈러 나눗셈이 균일한 방식으로 배열 인덱스를 생성하기 때문이죠. 즉, 소수에 의한 모듈러는 고정된 크기에 대해 가장 균등한 분배를 보장한다는 의미에요. 만약 4와 같이 소수가 아닌 작은 수에 의한 모듈러는 단지 0부터 3까지의 범위만을 보장하고 충돌이 자주 일어나죠.
밑의 key - value 쌍을 예로 봅시다.
{key: 7, value: 'hi'}
{key: 24, value: 'hello'}
{key: 42, value: 'sunny'}
{key: 34, value: 'weather'}
소수: 11
7 % 11 = 7
24 % 11 = 2
42 % 11 = 9
34 % 11 = 1

여기서 만약 키가 18인 자료를 해싱하게 된다면 인덱스 7에 이미 자료가 있으므로 충돌이 발생할 거에요. 충돌이 일어나지 않는 완벽한 해싱 함수가 있으면 좋겠지만, 그런 경우는 거의 불가능해요. 그래서 해시 테이블을 사용할 때는 충돌은 다루는 전략을 따로 세워야해요.
탐사 (Probling)
탐사 (Probling) 해싱 기법은 충돌이 발생하는 것을 피할 때, 배열에서 다음으로 사용 가능한 인덱스를 찾을 수 있게 해줘요. 이 중에서 선형 탐사 기법은 증분 시도를 통해 다음으로 사용 가능한 인덱스를 찾는 반면, 이차 탐사는 점진적으로 증분 시도를 생성하기 위해 이차 함수를 사용해요.
선형 탐사 (Linear Probling)
선형 탐사 는 한 번에 한 인덱스를 증가시킴으로써 사용 가능한 인덱스를 찾아요. 앞서 설명했던 것처럼 이미 인덱스 7이 차있을 때, 키 값 18이 들어오면 7 다음으로 빈 곳인 인덱스 8의 위치에 들어가게 돼요.

하지만 get() 함수를 사용할 때는 원래 해시 결과인 7부터 시작해서 18을 찾을 때까지 테이블을 순회해요. 이렇듯 선형 탐사는 군집을 쉽게 생성하는데, 이는 순회해야 할 자료를 더 만이 생성하기 때문에 단점으로 작용해요.
// Linear Probing
function HashTable(size) {
this.size = size;
this.limit = 0;
this.put = (key, value) => {
if (this.limit >= this.size) throw 'hash table is full';
let hashedIndex = this.hash(key);
while (this.keys[hashedIndex] !== null) {
hashedIndex++;
hashedIndex = hashedIndex % this.size;
}
this.keys[hashedIndex] = key;
this.values[hashedIndex] = value;
this.limit++;
}
this.get = key => {
let hashedIndex = this.hash(key);
while (this.keys[hashedIndex] !== key) {
hashedIndex++;
hashedIndex = hashedIndex % this.size;
}
return this.value[hashedIndex];
}
this.hash = key => {
// Check if the key is an integer
if (!Number.isInteger(key)) throw 'must be int';
return key % this.size;
}
this.initArray = size => {
const array = [];
for (let i = 0; i < size; i++) {
array.push(null);
}
return array;
}
this.keys = this.initArray(size);
this.values = this.initArray(size);
}// Test
const linearHash = new HashTable(13);
linearHash.put(7, 'hi');
linearHash.put(20, 'hello');
linearHash.put(33, 'sunny');
linearHash.put(46, 'weather');
linearHash.put(59, 'nice');
linearHash.put(72, 'cold');
linearHash.put(85, 'happy');
linearHash.put(98, 'sad');
console.log(linearHash.keys, linearHash.values);
이차 탐사 (Quadratic Probling)
이차 탐사 는 군집 문제를 해결하는데 좋은 기법이에요. 이차 탐사는 완전 제곱을 이용해서 사용 가능한 인덱스에 키를 균등하게 분배해요.

// Quadratic Probing
function HashTable(size) {
this.size = size;
this.limit = 0;
this.put = (key, value) => {
if (this.limit >= this.size) throw 'hash table is full';
let hashedIndex = this.hash(key), squareIndex = 1;
while (this.keys[hashedIndex] !== null) {
hashedIndex += Math.pow(squareIndex++, 2);
hashedIndex = hashedIndex % this.size;
}
this.keys[hashedIndex] = key;
this.values[hashedIndex] = value;
this.limit++;
}
this.get = key => {
let hashedIndex = this.hash(key), squareIndex = 1;
while (this.keys[hashedIndex] !== key) {
hashedIndex += Math.pow(squareIndex++, 2);
hashedIndex = hashedIndex % this.size;
}
return this.values[hashedIndex];
}
this.hash = key => {
// Check if the key is an integer
if (!Number.isInteger(key)) throw 'must be int';
return key % this.size;
}
this.initArray = size => {
const array = [];
for (let i = 0; i < size; i++) {
array.push(null);
}
return array;
}
this.keys = this.initArray(size);
this.values = this.initArray(size);
}// Test
const quadraticHash = new HashTable(13);
quadraticHash.put(7, 'hi');
quadraticHash.put(20, 'hello');
quadraticHash.put(33, 'sunny');
quadraticHash.put(46, 'weather');
quadraticHash.put(59, 'nice');
quadraticHash.put(72, 'cold');
quadraticHash.put(85, 'happy');
quadraticHash.put(98, 'sad');
console.log(quadraticHash.keys, quadraticHash.values);
결과 보시면 알겠지만, 이전 선형 탐사의 결과보다 키가 더 균등하게 분배됐을을 확인할 수 있어요. 여기서 만약 배열의 크기가 더 크고 더 많은 항목들이 있는 경우 차이는 더 극명하게 보일거에요.
재해싱 / 이중 해싱
키를 균일하게 분배하는 또 다른 좋은 방법으로는 이차 해싱 함수를 사용해서 원래 해싱 함수로부터 나온 결과를 한 번 더 해싱하는 방법이 있어요.
좋은 두번 째 해싱 함수의 요구 사항
1. 첫 번째 해싱 함수와 달라야 한다.
2. 시간 복잡도가 여전히 O(1)이어야 한다.
3. 함수의 결과가 0이 되어서는 안 된다.
일반적으로 사용되는 두 번째 해싱 함수는 hash(x) = R - (x % R) 이에요. 여기서 x 는 첫 번째 해싱 함수의 결과이고 R 은 해시 테이블의 크기보다 작은 값이에요.
아래는 이중 해싱과 선형 탐사를 조합한 코드에요.
// Double Hashing
function HashTable(size) {
this.size = size;
this.limit = 0;
this.put = (key, value) => {
if (this.limit >= this.size) throw 'hash table is full';
let hashedIndex = this.hash(key);
while (this.keys[hashedIndex] !== null) {
hashedIndex++;
hashedIndex = hashedIndex % this.size;
}
this.keys[hashedIndex] = key;
this.values[hashedIndex] = value;
this.limit++;
}
this.get = key => {
let hashedIndex = this.hash(key);
while (this.keys[hashedIndex] !== key) {
hashedIndex++;
hashedIndex = hashedIndex % this.size;
}
return this.values[hashedIndex];
}
this.hash = key => {
// Check if the key is an integer
if (!Number.isInteger(key)) throw 'must be int';
return this.secondHash(key % this.size);
}
this.secondHash = hashedKey => {
const R = this.size - 2;
return R - hashedKey % R;
}
this.initArray = size => {
const array = [];
for (let i = 0; i < size; i++) {
array.push(null);
}
return array;
}
this.keys = this.initArray(size);
this.values = this.initArray(size);
}// Test
const doubleHash = new HashTable(13);
doubleHash.put(7, 'hi');
doubleHash.put(20, 'hello');
doubleHash.put(33, 'sunny');
doubleHash.put(46, 'weather');
doubleHash.put(59, 'nice');
doubleHash.put(72, 'cold');
doubleHash.put(85, 'happy');
doubleHash.put(98, 'sad');
console.log(doubleHash.keys, doubleHash.values);캐싱 (Caching)
캐싱 (Caching) 은 자료를 임시 메모리에 저장하는 과정으로 추후에 해당 자료가 다실 필요할 때 쉽게 해당 자료를 얻을 수 있어요. 데이터베이스 시스템이 데이터를 캐싱해 하드 드라이브를 다시 읽는 작업을 피하는 것도 캐싱의 한 예에요. 또한 웹브라우저가 웹 페이지를 캐싱해 콘텐츠를 다시 다운로드하는 작업을 피하기도 해요.
간단히 얘기하자면 캐싱의 목표는 hit(필요한 항목이 캐시에 존재하는 경우)를 최대화하고 miss(필요한 항목이 캐시에 존재하지 않는 경우)를 최소화하는 것이에요. 이러한 캐싱 기법에는 LFU (Least Frequently Used) 캐싱 과 LRU (Least Recently Used) 캐싱 이 있어요.
캐시 설계는 최근에 접근한 메모리 위치를 다시 접근할 가능성인 시간적 지역성 과 최근에 접근한 메모리 위치 주변의 위치를 다시 접근할 가능성인 공간적 지역성 , 이 두가지를 주로 고려해요. 최적의 캐싱 알고리즘은 캐시에서 향후에 가장 나중에 사용될 부분을 신규로 삽입하고자 하는 항목으로 교체할 수 있어야 해요.
LFU 캐싱 (Least Frequently Used)
LFU 캐싱 은 운영체제가 메모리를 관리하기 위해 사용하는 캐싱 알고리즘이에요. 운영체제는 어떤 블록이 메모리에서 참조된 횟수를 관리하는데, 설계상 캐시가 자신의 한계를 초과하는 경우 운영체제는 가장 참조 빈도가 낮은 항목을 삭제해요.
LFU 캐시 를 가장 쉽게 구현하는 방법은 캐시에 로딩되는 모든 블록에 카운터를 할당하고 참조가 일어날 때마다 카운터를 증가시키는 것이에요. 이 처럼 LFU 캐싱은 직관적인 접근법처럼 보이겠지만, 메모리의 항목이 단시간에 반복적으로 참조된 다음 이후에 접근을 하지 않는 경우 이상적인 접근법이 아니에요. 해당 블록의 빈도가 높더라도 집중적으로 참조된 짧은 시간을 제외하면 자주 사용됐다고 보기 힘들기 때문에, 긴 시간 자주 사용된 블록들이 대신 삭제될 위험이 있어요. 게다가 신규 항목이 접근 빈도가 낮다는 이유로 삭제될 수도 있죠. 그래서 LFU를 사용할 때는 이러한 문제를 잘 고려해야 한답니다.
LFU 캐시는 이중 연결 리스트 를 사용해서 O(1) 시간에 항목을 제거해요. LFU에서 이중 연결 노드에는 freqCount 라는 속성이 있는데, 이는 해당 노드가 삽입된 다음에 해당 노드에 얼마자 자주 접근하는지를 보여줘요.
// LFU Caching
function LFUNode(key, value) {
this.prev = null;
this.next = null;
this.key = key;
this.data = value;
this.freqCount = 1;
}
function LFUDoublyLinkedList() {
this.head = new LFUNode('buffer head', null);
this.tail = new LFUNode('buffer tail', null);
this.head.next = this.tail;
this.tail.prev = this.head;
this.size = 0;
this.insertAtHead = node => {
node.next = this.head.next;
this.head.next.prev = node;
this.head.next = node;
node.prev = this.head;
this.size++;
}
this.removeAtTail = () => {
const oldTail = this.tail.prev;
const prev = this.tail.prev;
prev.prev.next = this.tail;
this.tail.prev = prev.prev;
this.size--;
return oldTail;
}
this.removeNode = node => {
node.prev.next = node.next;
node.next.prev = node.prev;
this.size--;
}
}
function LFUCache(capacity) {
this.keys = {}; // LFUNode를 저장한다.
this.freq = {}; // LFUDoubleLinkedList를 저장한다.
this.capacity = capacity;
this.minFreq = 0;
this.size = 0;
this.set = (key, value) => {
let node = this.keys[key];
if (node === undefined) {
node = new LFUNode(key, value);
this.keys[key] = node;
if (this.size !== this.capacity) {
// 삭제 없이 삽입
if (this.freq[1] === undefined) {
this.freq[1] = new LFUDoublyLinkedList();
}
this.freq[1].insertAtHead(node);
this.size++;
} else {
// 삭제 후 삽입하기
let oldTail = this.freq[this.minFreq].removeAtTail();
delete this.keys[oldTail.key];
if (this.freq[1] === undefined) {
this.freq[1] = new LFUDoublyLinkedList();
}
this.freq[1].insertAtHead(node);
}
this.minFreq = 1;
} else {
let oldFreqCount = node.freqCount;
node.data = value;
node.freqCount++;
this.freq[oldFreqCount].removeNode(node);
if (this.freq[node.ferqCount] === undefined) {
this.freq[node.ferqCount] = new LFUDoublyLinkedList();
}
this.freq[node.freqCount].insertAtHead(node);
if (oldFreqCount === this.minFreq && Object.keys(this.freq[oldFreqCount]).size === 0) {
this.minFreq++;
}
}
}
this.get = key => {
const node = this.keys[key];
if (node === undefined) {
return null;
} else {
const oldFreqCount = node.freqCount;
node.freqCount++;
this.freq[oldFreqCount].removeNode(node);
if (this.freq[node.freqCount] === undefined) {
this.freq[node.freqCount] = new LFUDoublyLinkedList();
}
this.freq[node.freqCount].insertAtHead(node);
if (oldFreqCount === this.minFreq && Object.keys(this.freq[oldFreqCount]).length === 0) {
this.minFreq++;
}
return node.data;
}
}
}// Test
const myLFU = new LFUCache(5);
myLFU.set(1, 1); // myLFU.freq 상태: {1: 1}
myLFU.set(2, 2); // myLFU.freq 상태: {1: 2 <-> 1}
myLFU.set(3, 3); // myLFU.freq 상태: {1: 3 <-> 2 <-> 1}
myLFU.set(4, 4); // myLFU.freq 상태: {1: 4 <-> 3 <-> 2 <-> 1}
myLFU.set(5, 5); // myLFU.freq 상태: {1: 5 <-> 4 <-> 3 <-> 2 <-> 1}
myLFU.get(1); // 1을 반환. myLFU.freq 상태: {1: 5 <-> 4 <-> 3 <-> 2, 2: 1}
myLFU.get(1); // 1을 반환. myLFU.freq 상태: {1: 5 <-> 4 <-> 3 <-> 2, 3: 1}
myLFU.get(1); // 1을 반환. myLFU.freq 상태: {1: 5 <-> 4 <-> 3 <-> 2, 4: 1}
myLFU.set(6, 6); // myLFU.freq 상태: {1: 6 <-> 5 <-> 4 <-> 3, 4: 1}
myLFU.get(6); // 1을 반환. myLFU.freq 상태: {1: 5 <-> 4 <-> 3, 4: 1, 2: 6}LRU 캐싱 (Least Recently Used)
LRU 캐싱 은 가장 오래된 항목을 먼저 제거하는 캐싱 알고리즘이에요. 만약 캐시의 항목에 접근하면 해당 항목은 리스트의 뒤로 이동해요. 하지만 캐시에 없는 항목에 접근한다면 가장 앞에 있는 항목이 삭제되고 새로운 항목이 리스트 뒤에 추가되죠. 즉 교체될 항목은 가장 오래전에 접근한 항목이겠죠.
LRU 알고리즘 을 구현하기 위해서는 어떤 노드가 언제 사용되었는지를 관리해야 해요. 이를 구현하기 위해 LFU 캐시는 이중 연결 리스트 와 해시 테이블 을 사용하죠.
이중 연결 리스트는 헤드(가장 오래된 항목) 를 추적할 때 필요해요. 새로운 자료가 추가될 때마다 이중 연결 리스트의 크기를 초과할 때까지 헤드를 위로 이동시키는데, 이동 중 리스트의 크기를 초과하게 되면 가장 오래된 자료가 제거되죠.
// LRU Caching
function DLLNode(key, data) {
this.key = key;
this.data = data;
this.next = null;
this.prev = null;
}
function LRUCache(capacity) {
this.keys = {};
this.capacity = capacity;
this.head = new DLLNode('', null);
this.tail = new DLLNode('', nll);
this.head.next = this.tail;
this.tail.prev = this.head;
this.removeNode = node => {
const prev = next.prev, next = node.next;
prev.next = next;
next.prev = prev;
}
this.addNode = node => {
const realTail = this.tail.prev;
realTail.next = node;
this.tail.prev = node;
node.prev = realTail;
node.next = this.tail;
}
this.get = key => {
const node = this.keys[key];
if (node === undefined) {
return null;
} else {
this.removeNode(node);
this.addNode(node);
return node.data;
}
}
this.set = (key, value) => {
const node = this.keys[key];
if (node) {
this.removeNode(node);
}
const newNode = new DLLNode(key, value);
this.addNode(newNode);
this.keys[key] = newNode;
// 노드를 제거
if (Object.keys(this.keys).length > this.capacity) {
const realHead = this.head.next;
this.removeNode(realHead);
delete this.keys[realHead.key];
}
}
}// Test
const myLRU = new LRUCache(5);
myLFU.set(1, 1); // 1 <-> 1
myLFU.set(2, 2); // 1 <-> 2
myLFU.set(3, 3); // 1 <-> 2 <-> 3
myLFU.set(4, 4); // 1 <-> 2 <-> 3 <-> 4
myLFU.set(5, 5); // 1 <-> 2 <-> 3 <-> 4 <-> 5
myLFU.get(1); // 2 <-> 3 <-> 4 <-> 5 <-> 1
myLFU.get(2); // 3 <-> 4 <-> 5 <-> 1 <-> 2
myLFU.set(6, 6); // 4 <-> 5 <-> 1 <-> 2 <-> 6
myLFU.set(7, 7); // 5 <-> 1 <-> 2 <-> 6 <-> 7
myLFU.set(8, 8); // 1 <-> 2 <-> 6 <-> 7 <-> 8이 외에도 NRU(Not Recently Used) 알고리즘 이나 선입선출 알고리즘 과 같이 다른 캐싱 알고리즘들이 있지만, 대부분의 경우 LRU보다 성능이 떨어져요. 그 만큼 LRU가 우리가 사용하는 시스템의 동작 방식과 작업량을 고려할 때 가장 효과적인 알고리즘이라는 얘기겠죠.
힙 (Heap)
힙 (Heap) 은 트리와 비슷한 자료 구조의 일종으로, 최대 힙의 경우 부모가 자식보다 크고 최소 힙의 경우 보모가 자식보다 작아요. 이러한 힙의 특성은 자료를 정렬하는데 유용하답니다. 힙은 자식에 대한 포인터를 갖는 대신에 배열 을 사용해 자료를 저장해요. 힙을 사용하면 부모와 자식 간의 관계를 쉽게 정의 할 수 있기에, 배열에서 힙 노드의 자식 위치(인덱스)를 쉽게 계산할 수 있죠.
힙 에는 다양한 수의 자식을 갖는 다양한 종류가 있어요. 힙은 배열을 사용해 자료를 저장하기 때문에 배열의 인덱스는 각 항목의 차수/높이를 정의해요. 첫번 째 배열 항목을 루트로 설정한 다음 각 왼쪽 항목과 오른쪽 항목을 순서대로 채움으로써 이진 힙 을 만들 수 있어요.
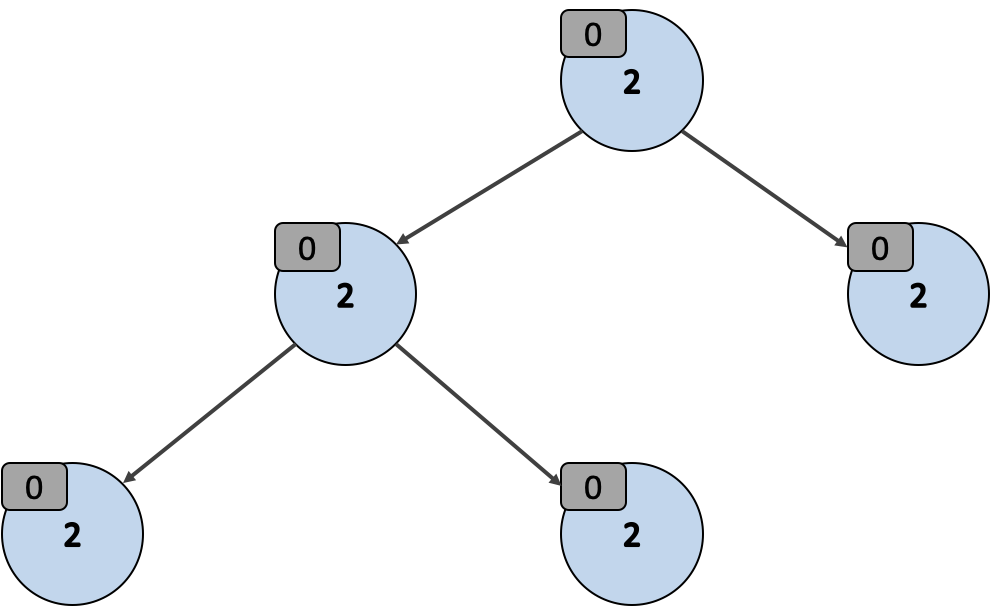
최대 힙과 최소 힙 두 종류의 이진 힙이 있을 때, 최대 힙 의 경우 루트 노드가 가장 높은 값을 갖고 각 노드의 값이 자식의 값보다 커요. 반대로 최소 힙 의 경우 루트 노드가 가장 낮은 값을 갖고 각 노드의 값이 자식의 값보다 작죠.
힙은 문자열과 정수, 심지어 사용자 정의 클래스와 같이 어떤 종류의 값이든 저장할 수 있어요. 그리고 자바스크립트는 문자열과 정수 값 비교를 기본적으로 지원하고 있죠. 하지만 사용자 정의 클래스의 경우 개발자가 두 클래스를 비교할 방법을 직접 구현해야 돼요.
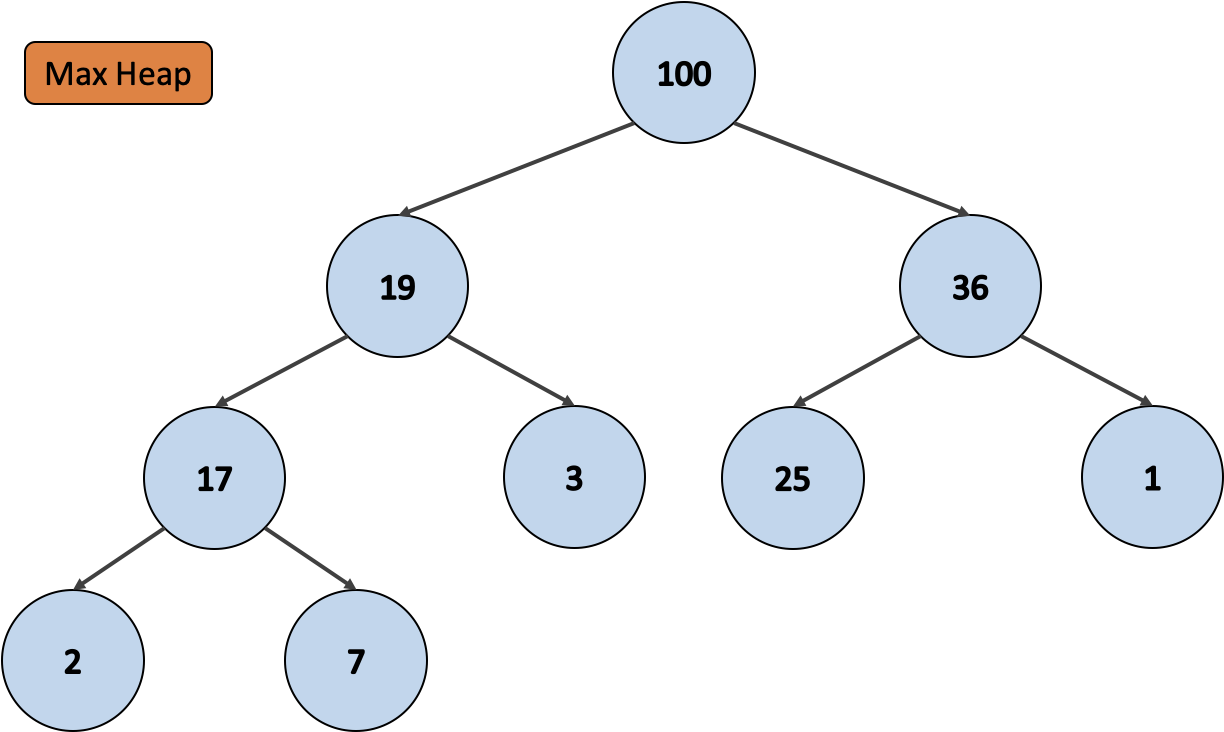
앞에서 설명했다싶이 최대 힙 은 부모가 모든 자식보다 항상 큰 힙이에요. 그림과 같은 이진 힙이 존재할 때, 최대 힙의 배열은 [100, 19, 36, 17, 3, 25, 1, 2, 7] 이에요.
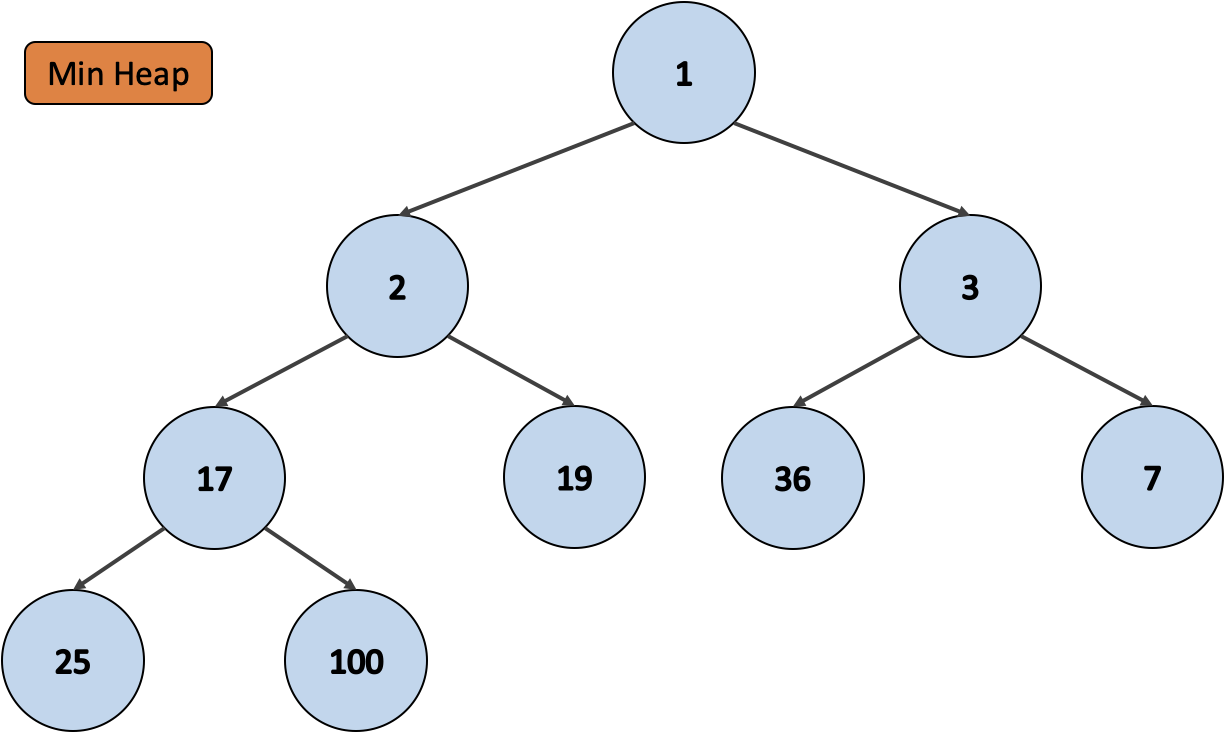
최소 힙 은 부모가 모든 자식보다 항상 작은 힙이에요. 그림과 같은 이진 힙이 존재할 때, 최소 힙의 배열은 [1, 2, 3, 17, 19, 36, 7, 25, 100] 이죠.
이진 힙 (Binary Heap)
이진 힙 (Binary Heap) 의 경우 힙을 나타내기 위해 배열이 사용되는데 다음과 같이 인덱스를 사용해요. 이 때, N은 노드의 인덱스에요.
자신 노드: N
부모 노드: (N - 1) / 2
왼쪽 자식 노드: 2 n + 1
오른쪽 자식 노드: 2 n + 2
// Binary Heap
function Heap() {
this.items = [];
this.swap = (index1, index2) => {
[this.items[index1], this.items[index2]] = [this.items[index2], this.items[index1]];
};
this.parentIndex = index => {
return Math.floor((index - 1) / 2);
};
this.leftChildIndex = index => {
return index * 2 + 1;
};
this.rightChildIndex = index => {
return index * 2 + 2;
};
this.parent = index => {
return this.items[this.parentIndex(index)];
};
this.leftChild = index => {
return this.items[this.leftChildIndex(index)];
};
this.rightChild = index => {
return this.items[this.rightChildIndex(index)];
};
this.peek = item => {
return this.items[0];
};
this.size = () => {
return this.items.length;
};
}삼투 과정
항목을 추가하거나 삭제할 때는 힙의 구조가 유지 되어야 해요. 이를 위해 항목 간에 교환이 일어나서 마치 비누 거품이 위로 올라가듯이 힙의 꼭대기로 점차 올라가야 해요. 마찬가지로 일부 항목들은 힙의 구조를 유지하기 위해 올바른 위치로 마치 비누 거품이 땅으로 내려가듯이 내려가야 해요. 이러한 노드 간 전파의 시간 복잡도는 O(log2(n))이에요
12, 2, 23, 4, 13 순으로 값을 최소 힙에 삽입해 봅시다.
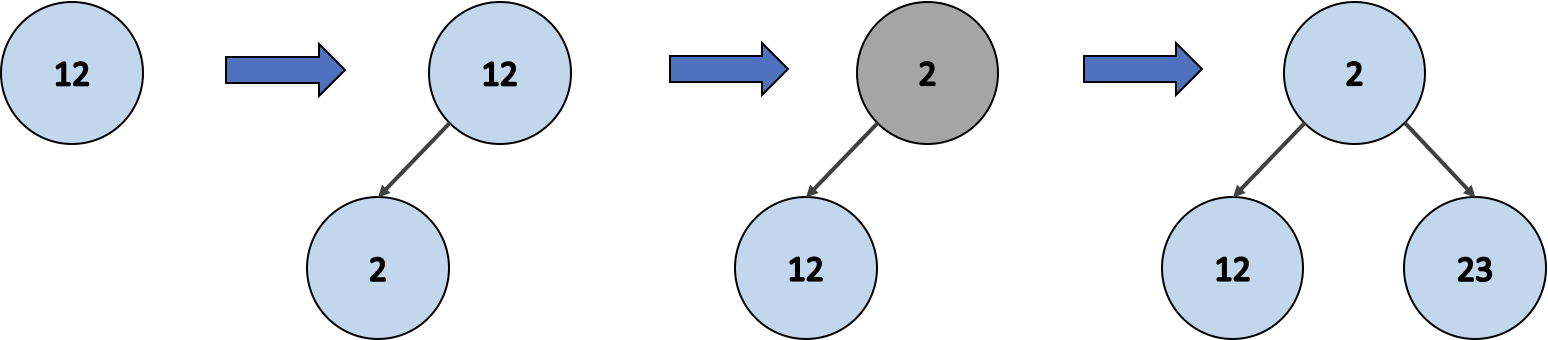
- 첫 번째 노드 12를 삽입한다.
- 새로운 노드 2를 삽입한다.
- 최소 힙 구조를 유지하기 위해 노드 2가 최상위로 올라간다.
- 새로운 노드 23을 삽입한다.
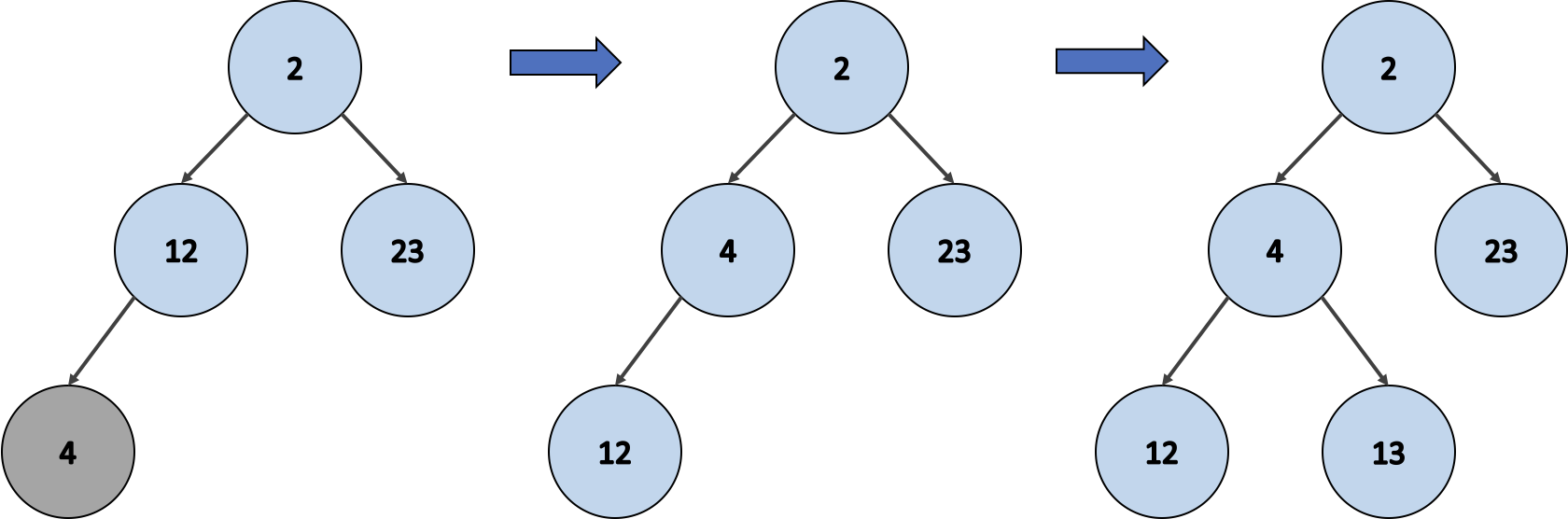
- 새로운 노드 4를 삽입한다.
- 최소 힙 구조를 유지하기 위해 노드 12와 노드 4의 위치를 교환한다.
- 새로운 노드 12를 삽입한다.
이를 통해 힙 배열 [2, 4, 23, 12, 13] 이 완성 되었어요.
삼투의 위 아래 이동을 구현하기 위해서는 취소 힙 구조의 제일 위에 최솟값 항목이 위치할 때까지 항목들을 교환해야 해요. 아래로 이동하기 위해서는 최상위 항목(배열의 첫 번째 항목)을 자식 중 하나와 교환해야 하죠. 마찬가지로 위로 이동하기 위해서는 신규 항목의 부모가 신규 항목보다 큰 경우 부모와 신규 항목이 교환 되어야 한답니다.
// Min Heap
function MinHeap() {
this.items = [];
this.bubbleDown = () => {
let index = 0;
while (this.leftChild(index) && this.leftChild(index) < this.items[index]) {
let smallerIndex = this.leftChildIndex(index);
if (this.rightChile(index) && this.rightChild(index) < this.items[smallerIndex]) {
smallerIndex = this.rightChildIndex(index);
}
this.swap(smallerIndex, index);
index = smallerIndex;
}
};
this.bubbleUp = () => {
let index = this.items.length - 1;
while (this.parent(index) && this.parent(index) > this.items[index]) {
this.swap(this.parentIndex(index), index);
index = this.parentIndex(index);
}
};
}최대 힙 구현은 최소 힙 구현과 비교자 부분만 달라요. 아래로 이동하기 위해서 최대 힙 노드는 자식이 자신보다 큰 경우에 교환하죠. 마찬가지로 위로 이동하기 위해서 가장 최근에 삽입된 노드는 부모 노드가 자신보다 작은 경우에 부모 노드와 교환돼요.
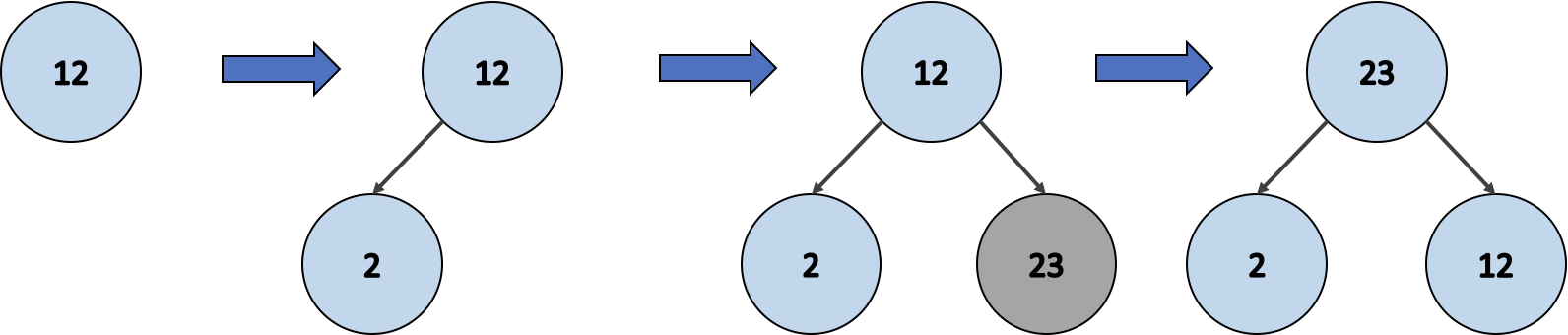
- 첫 번째 노드 12를 삽입한다.
- 새로운 노드 2를 삽입한다.
- 새로운 노드 23을 삽입한다.
- 최대 힙 구조를 유지하기 위해 노드 23이 최상위로 올라간다.
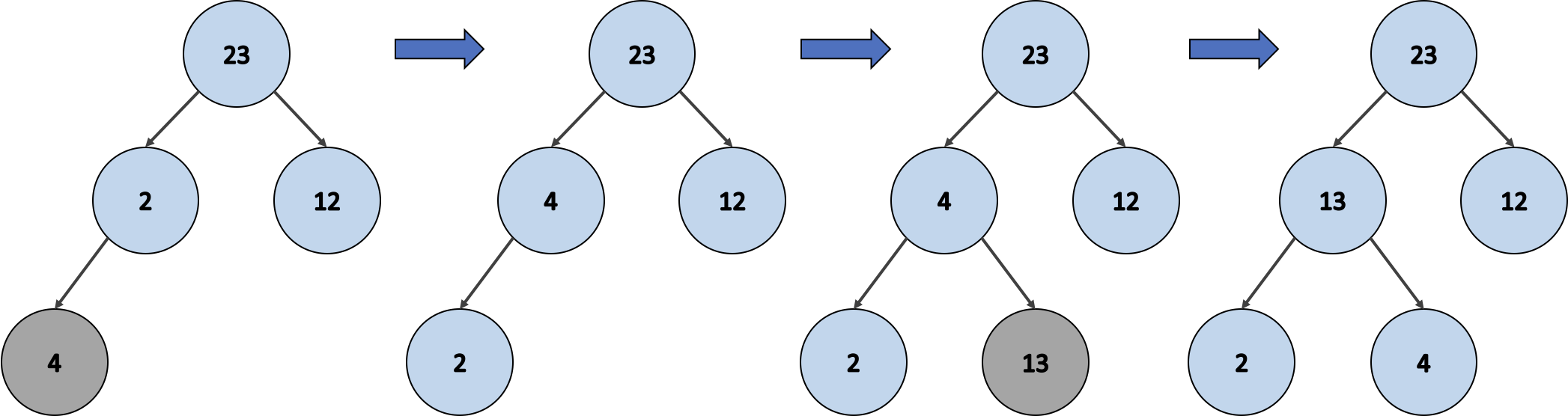
- 새로운 노드 4를 삽입한다.
- 최대 힙 구조를 유지하기 위해 노드 4와 노드 2의 위치를 교환한다.
- 새로운 노드 13을 삽입한다.
- 최대 힙 구조를 유지 하기 위해 노드 13과 노드 4의 위치를 교환한다.
위의 힙의 배열 내용으로 배열 [23, 13, 12, 2, 4] 이 생성 되었어요.
힙 정렬
힙 클래스를 생성한 뒤엔 힙을 사용해 정렬 하는 것이 꽤 간단해요. 힙이 빈 상태가 될 때까지 힙 배열을 pop() 하여 꺼낸 객체를 저장하면 정렬된 배열을 얻을 수 있죠. 이를 힙 정렬이라 한답니다. 힙 정렬의 시간 복잡도는 빠른 정렬이나 병합 정렬과 같은 O(log2(n))이에요.
오름차순 정렬 (최소 힙)
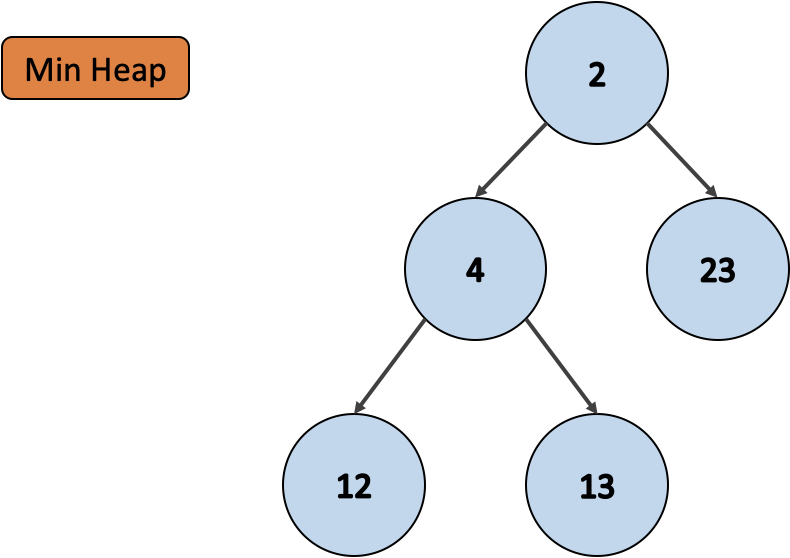
const myMinHeap = new MinHeap();
myMinHeap.add(12);
myMinHeap.add(2);
myMinHeap.add(23);
myMinHeap.add(4);
myMinHeap.add(13);
myMinHeap.items; // [2, 4, 23, 12, 13]위는 최소 힙 클래스를 통해 만들어진 배열이에요. 이제 이 최소 힙 배열을 pop() 을 통해 항목들을 꺼내어 힙을 재구성할거에요. 최종적으로 힙이 빈 상태가 되면 정렬 이 완료된 것입니다.
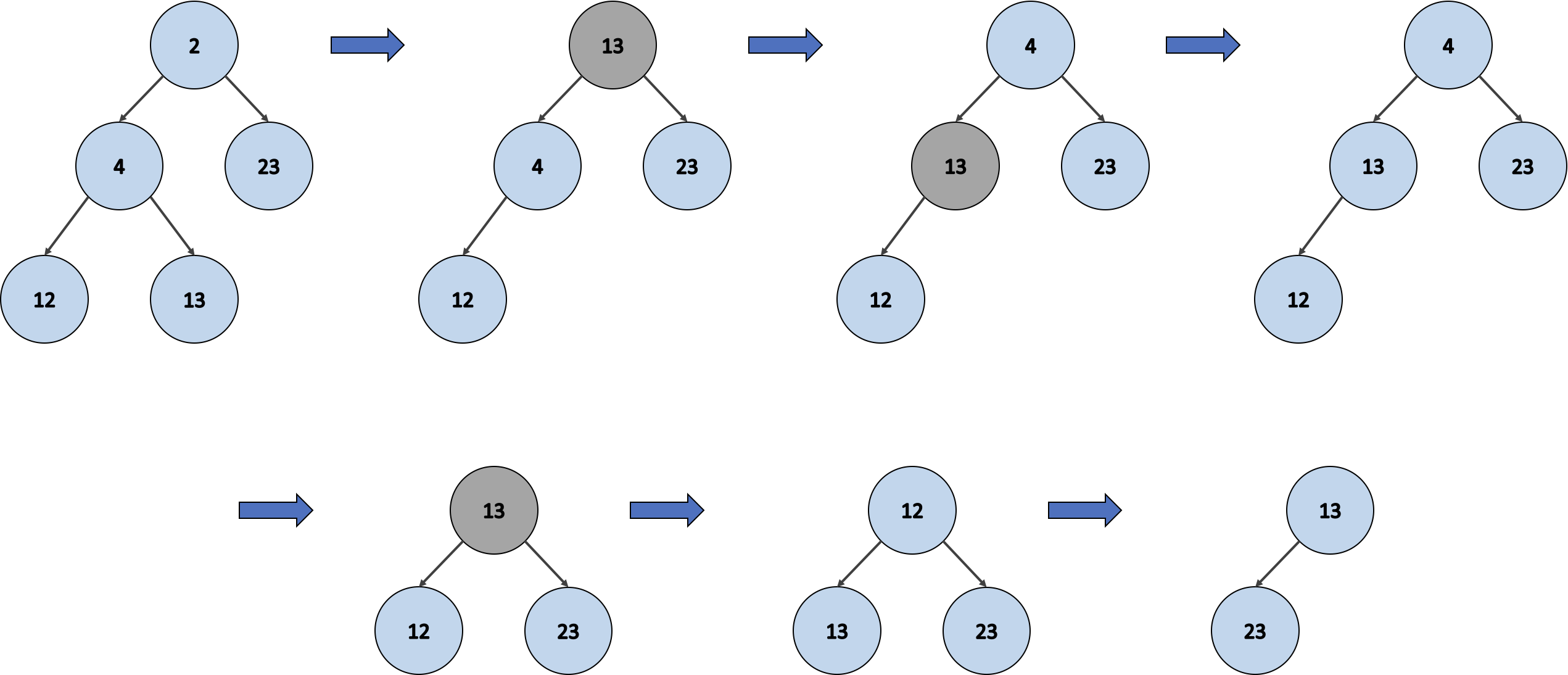
console.log(myMinHeap.poll()); // 2
console.log(myMinHeap.poll()); // 4
console.log(myMinHeap.poll()); // 12
console.log(myMinHeap.poll()); // 13
console.log(myMinHeap.poll()); // 23위에서 보듯이 항목을 꺼내는 과정에서 삼투도 같이 일어나고 마침내 정렬이 끝납니다.
내림차순 정렬 (최대 힙)
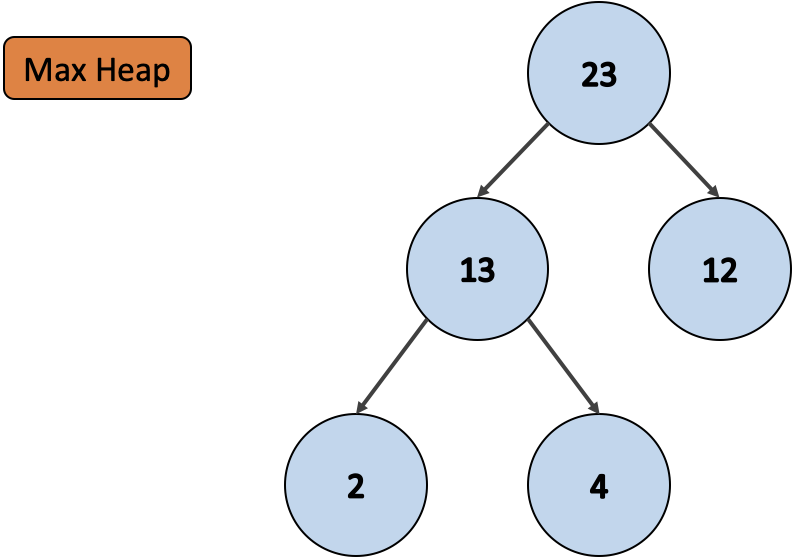
const myMaxHeap = new MaxHeap();
myMaxHeap.add(12);
myMaxHeap.add(2);
myMaxHeap.add(23);
myMaxHeap.add(4);
myMaxHeap.add(13);
myMaxHeap.items; // [23, 13, 12, 2, 4]최소 힙과 마찬가지로 위는 최대 힙 클래스를 통해 만들어진 배열이에요. 이 최대 힙 배열도 항목들을 꺼냄에 따라 최대 힙이 재구성돼요. 그리고 최종적으로 최대 힙이 빈 경우 정렬 이 완료됩니다.
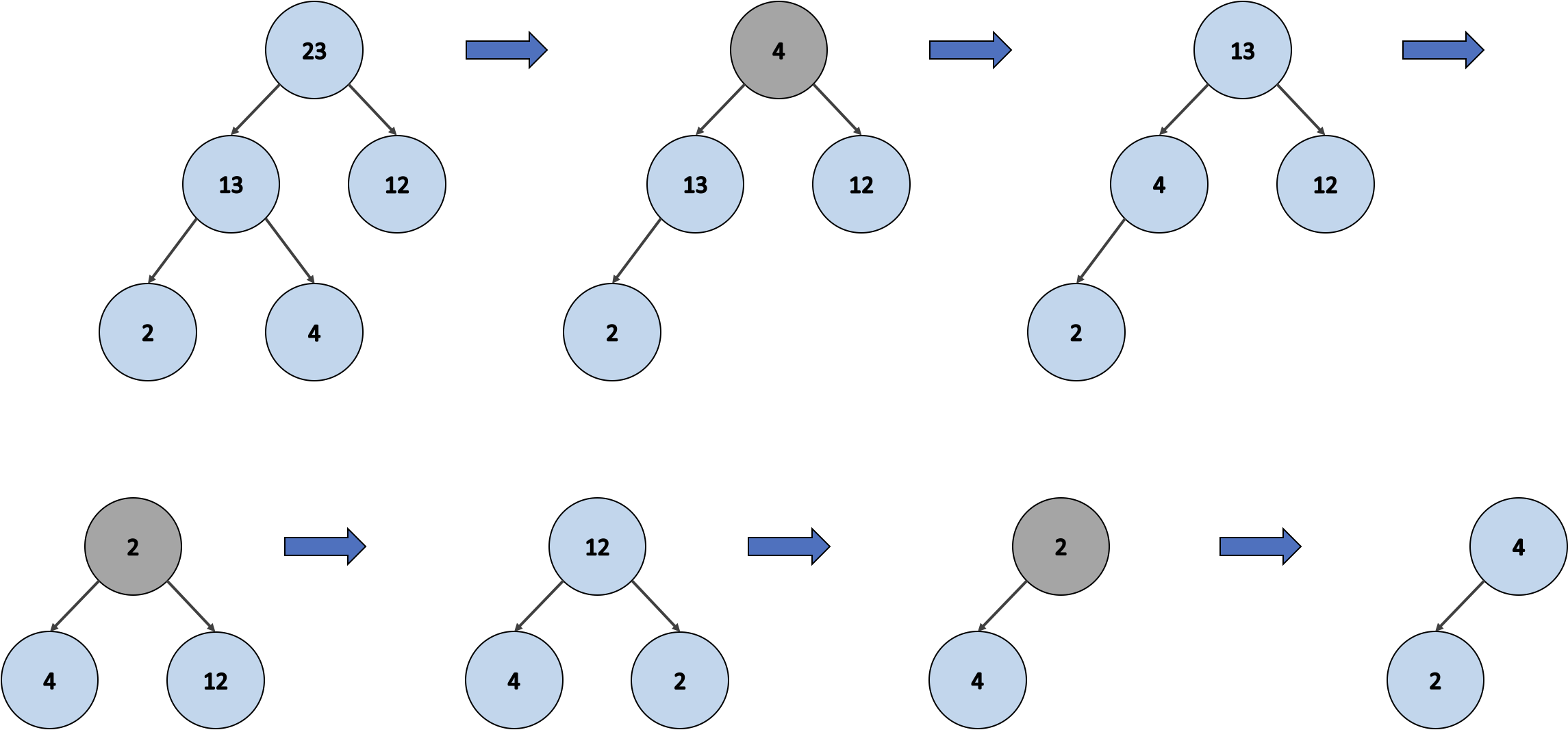
console.log(myMaxHeap.poll()); // 23
console.log(myMaxHeap.poll()); // 13
console.log(myMaxHeap.poll()); // 12
console.log(myMaxHeap.poll()); // 2
console.log(myMaxHeap.poll()); // 4이 처럼 최대 힙 정렬도 완료되었습니다.
참고 자료
- 오주영, 『(Javascript로 배우는) 자료구조』, 에듀컨텐츠휴피아(2019)
- 배세민, 『자바스크립트로 하는 자료 구조와 알고리즘 : 핵심 자료구조 및 알고리즘을 이해하고 구현하기 위한 입문서』, 에이콘(2019)
