---

트리 (Tree)

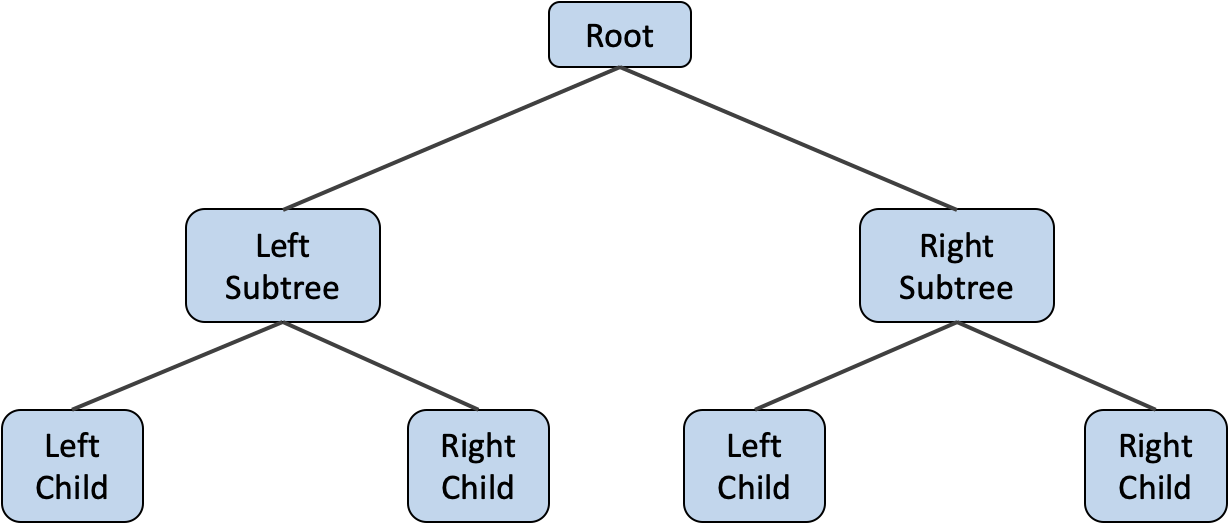
트리 (Tree) 는 하나의 루트 노드를 가지며, 자료들을 이루는 자료 객체들 사이의 계급적 구조를 간선에 의해 표현하는 비선형 자료구조에요. 트리 구조에서 만약 루트 노드를 제거한다면, 루트 노드로부터 파생되는 트리군이 형성돼요. 이 때 생성된 트리군을 루트 노드의 부트리(subtree)라고 해요. 트리는 노드간의 사이클이 존재하지 않는 그래프의 부분집합이랍니다.

트리의 종류

순서 트리

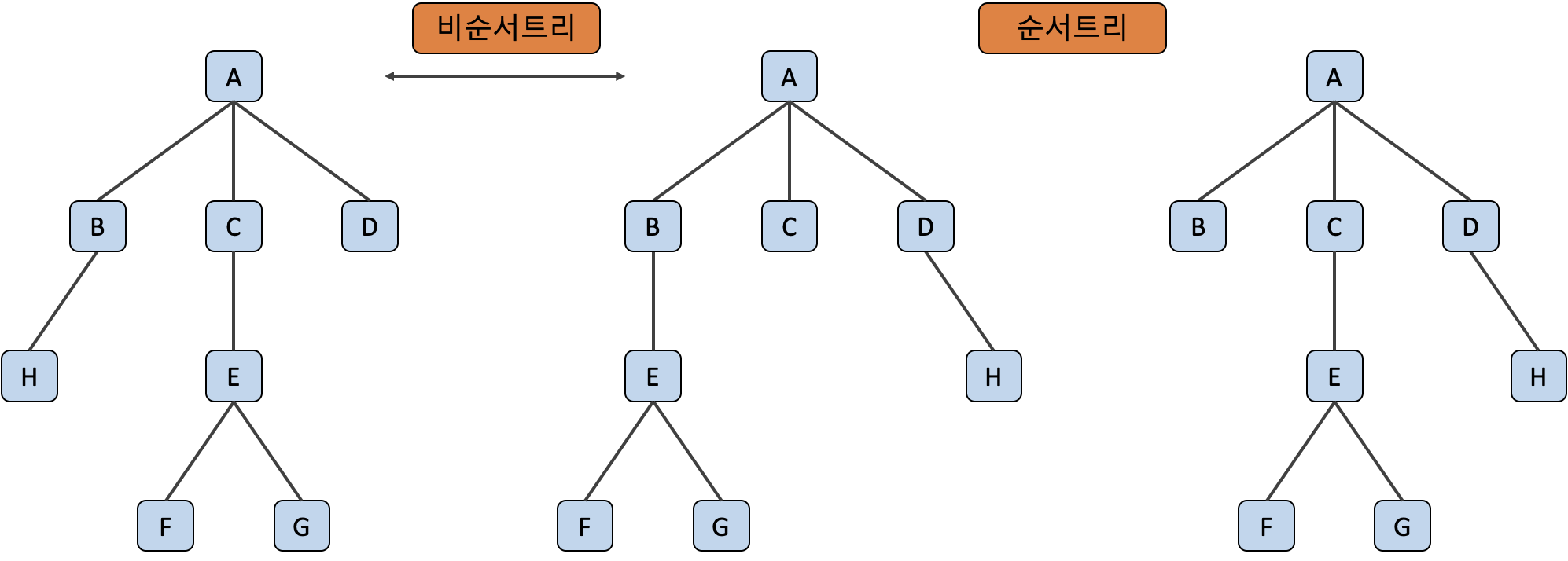
순서 트리 는 레벨이 같은 노드들의 좌우 배열 순서의 위치가 고정되어 위치상 의미가 중요한 트리에요.

닮은 트리와 대등한 트리

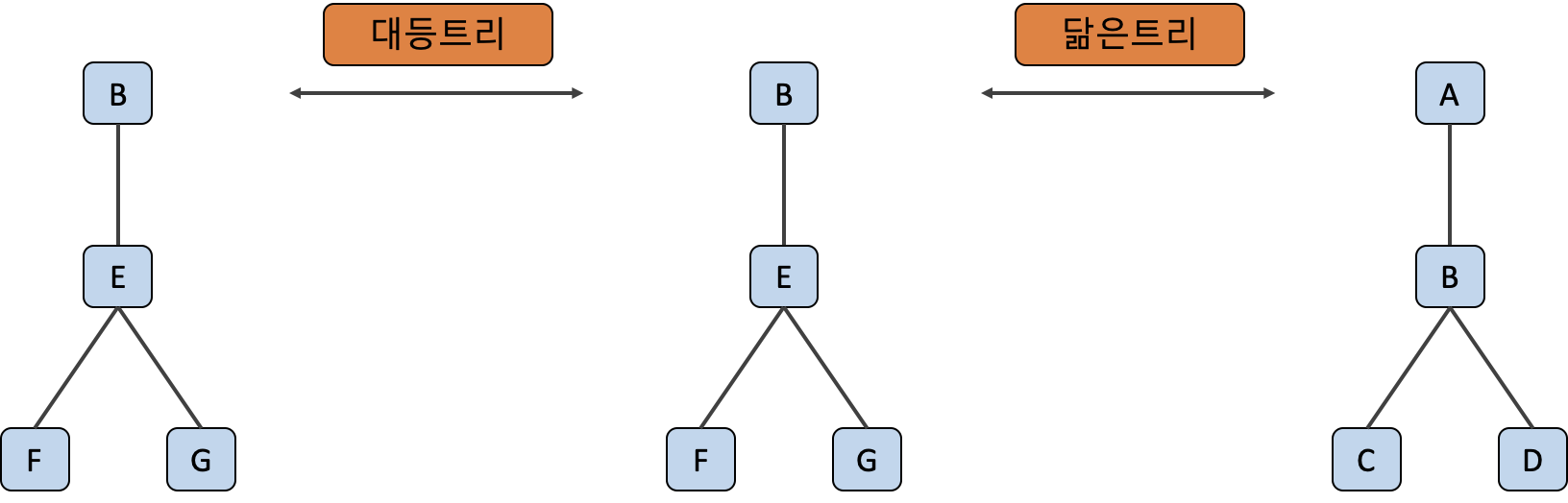
닮은 트리 는 트리의 노드수와 위치 등 구조는 같고 노드의 자료부분만 다른 트리를 말합니다. 이와 달리 대등한 트리 는 트리의 구조와 위치, 자료들이 모두 동일한 트리에요.

오리엔티드 트리

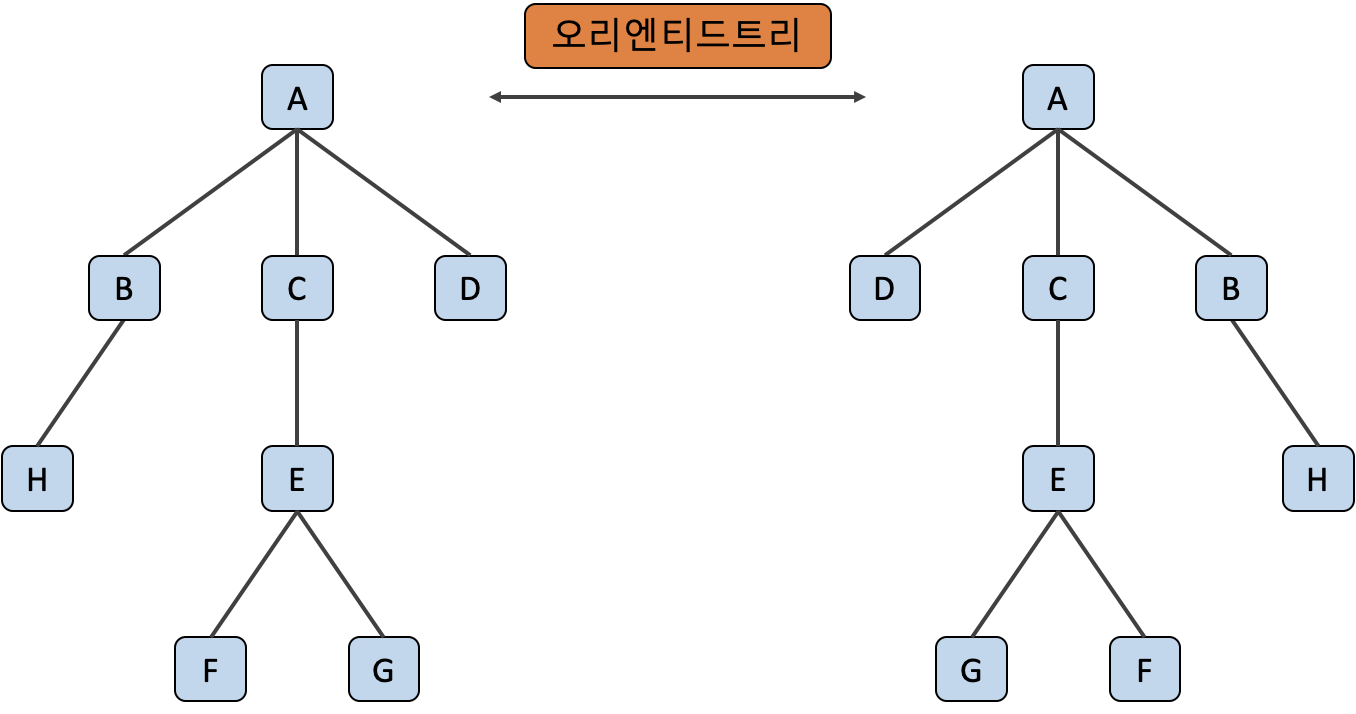
오리엔티드 트리 는 각 노드의 순서가 고정되어 있지 않고, 위치상의 의미가 중요하지 않은 트리에요. 각 트리의 깊이가 동일하고, 선행 노드와 후행 노드간의 관계만 동일하면 오리엔티드 트리 관계가 됩니다.

트리의 저장법

배열을 이용한 저장

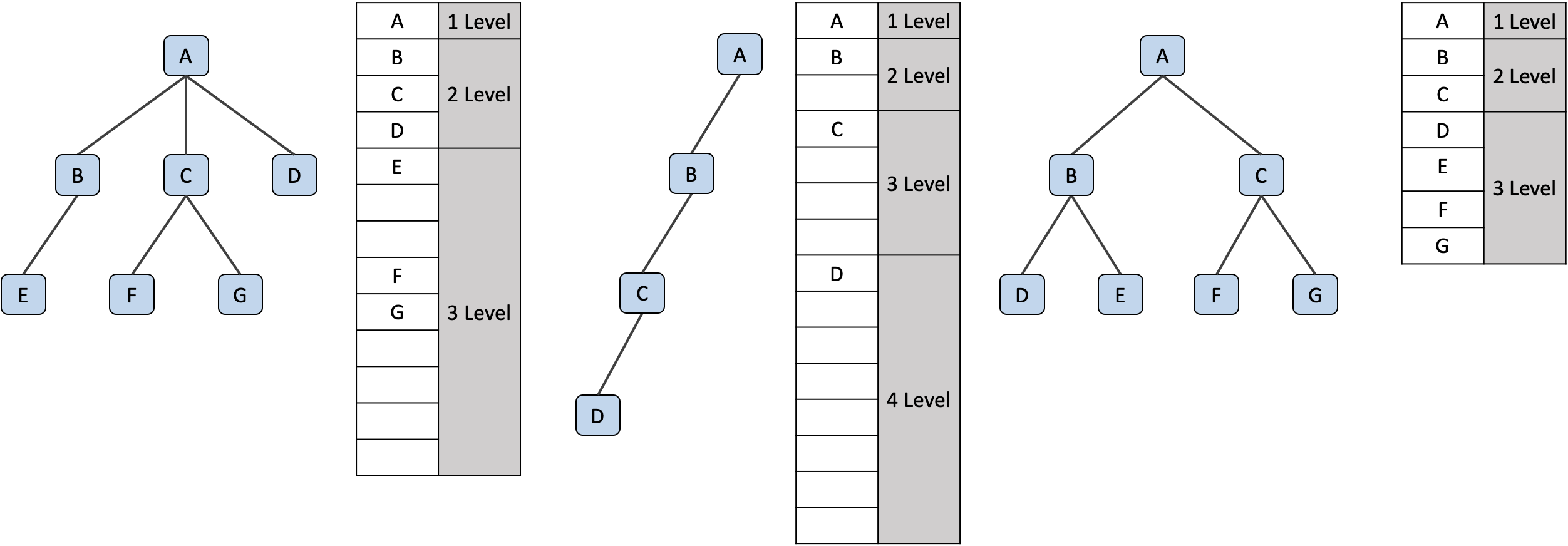
트리구조를 배열 을 통해 저장할 때는 루트 노드부터 레벨과 좌우 순서에 따라 저장해요. 때문에 공간 낭비가 생기지 않도록 자식 노드들을 잘 배분해야겠죠.

연결 리스트를 이용한 저장

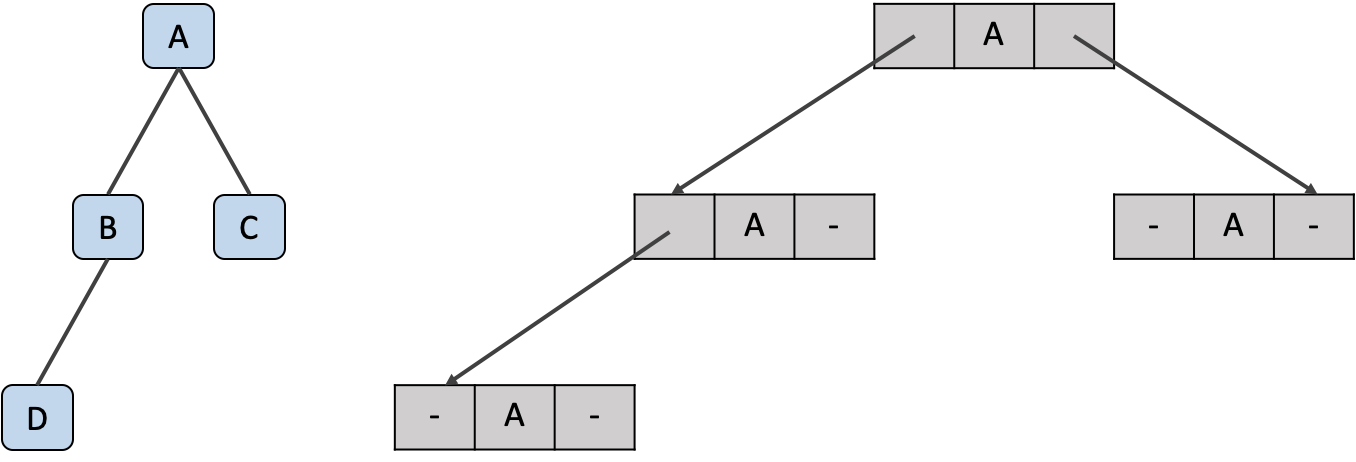
이진 트리의 노드와 가지들을 연결 리스트 의 노드와 포인터로 대응하여 저장하는 방법도 있어요. 이 때 리스트는 자료 필드와 두 개의 링크 필드로 구성됩니다.

이진 트리 (Binary Tree)

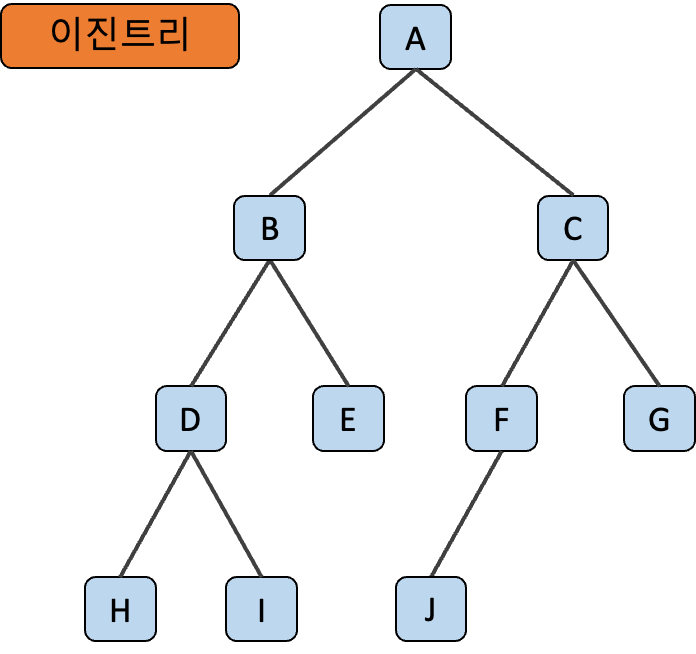
이진 트리 (Binary Tree) 는 트리를 구성하는 모든 노드의 가지수가 2 이하로 구성된 트리에요. 그리고 이진 트리는 각 노드들의 좌우 순서가 중요한 의미를 지니기 때문에 순서 트리라고 할 수 있습니다.

이진 트리는 검색 시간과 링크에 의해 낭비되는 공간을 최소화하기 쉽기 때문에 일반 트리를 이진 트리로 변환하기도 해요.

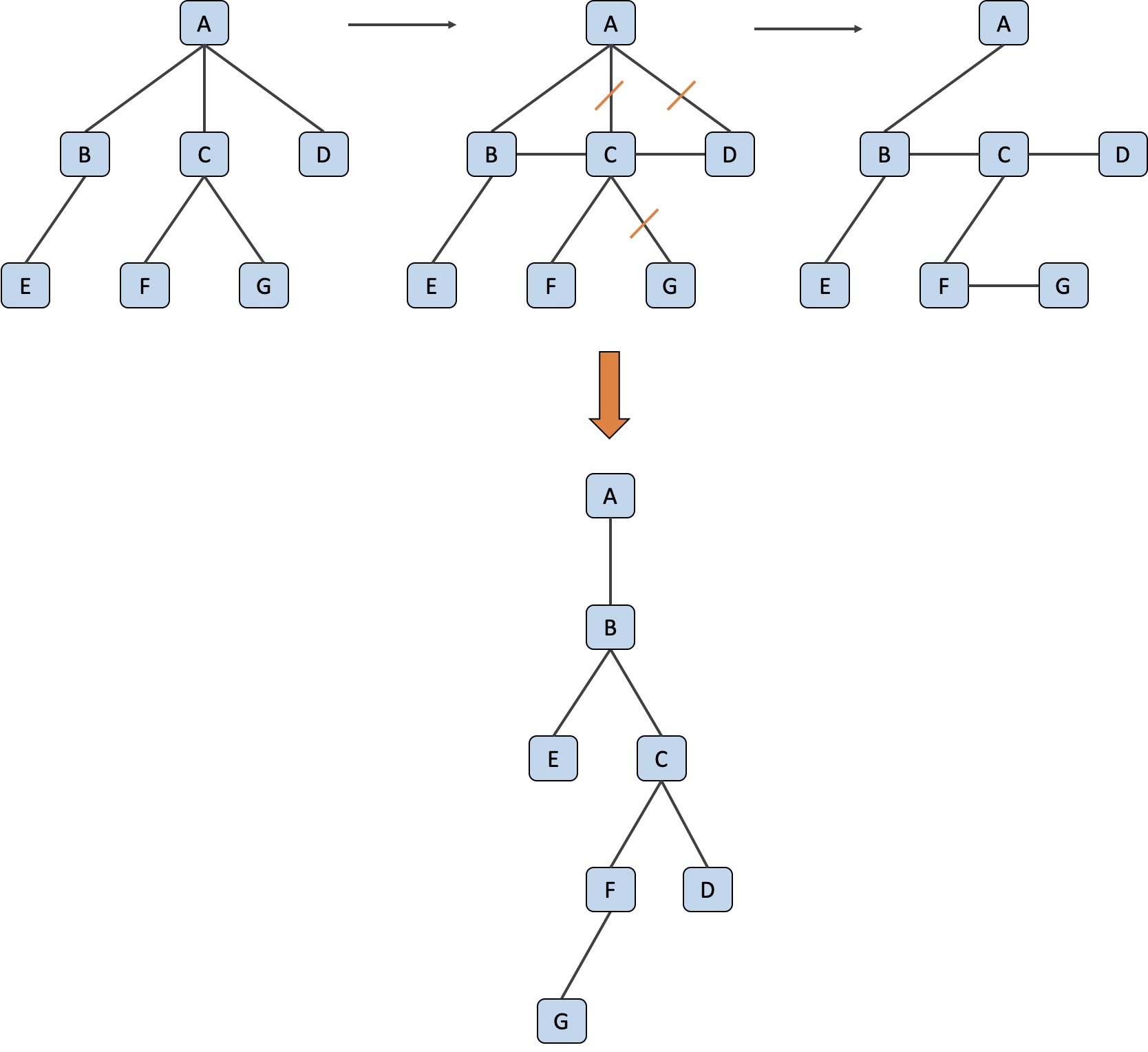
이진 트리로의 변환
1단계 : 형제노드(Sibling)끼리 연결한다.
2단계 : 연결된 동료노드 간의 가지는 그대로 두고, 부모노드와 자식노드의 연결 가지 중에서 가장 왼쪽의 자식 노드를 연결시킨 가지만 제외하고 나머지 가지들을 모두 삭제한다.

이러한 이진 트리를 운행하는 방법에는 크게 세 가지가 있어요. 이는 각각 전위 운행 , 중위 운행 , 후위 운행 이에요.

전위 운행 (Preorder Traversal)

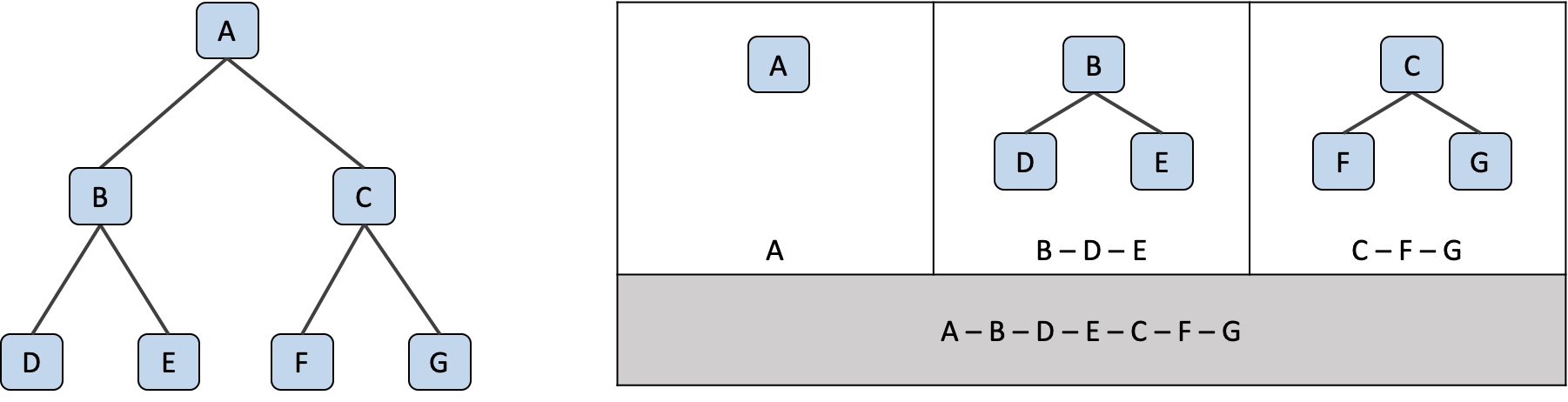
Root > Left > Right

전위 운행 은 제일 먼저 루트 노드를 방문한 뒤, 이후 나오는 자식노드들에서 계속해서 왼쪽 가지를 따라 운행해요. 만약 왼쪽 가지를 따라 운행 중에 더 이상 자식 노드가 없다면, 오른쪽 형제 노드로 향하여 다시 왼쪽 가지를 따라 운행 해요.

중위 운행 (Inorder Traversal)

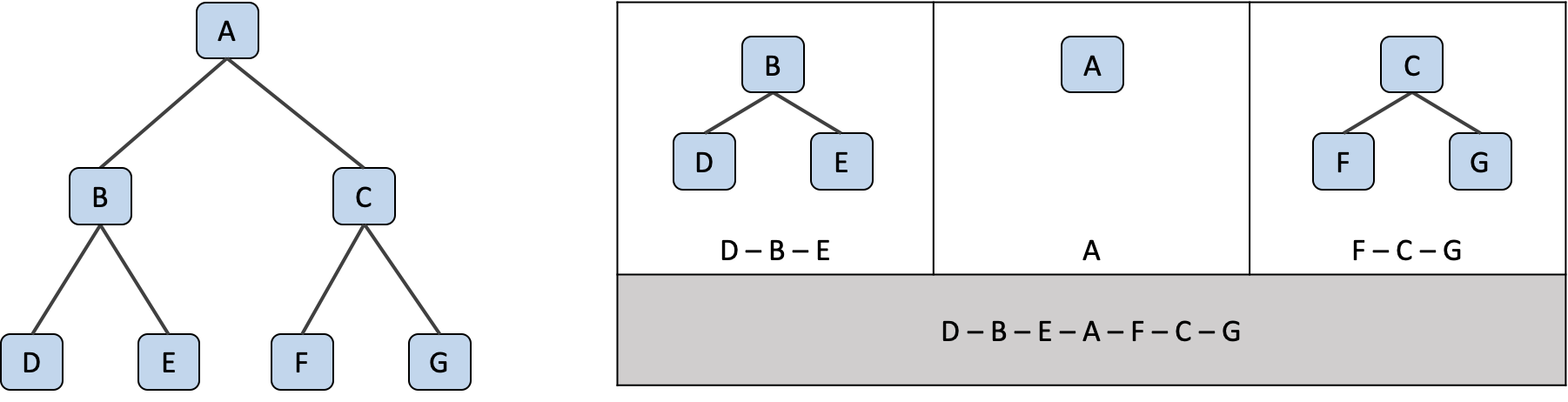
Left > Root > Right

중위 운행 은 가장 깊은 레벨의 가장 왼쪽 노드부터 운행을 시작해요. 그 다음 다시 바로 위의 부모 노드로 돌아가, 오른쪽 형제 노드에서 앞에서 했던 것처럼 가장 깊은 레벨의 왼쪽 노드를 운행해요. 이 과정을 계속 반복하면 됩니다.

후위 운행 (Postorder Traversal)

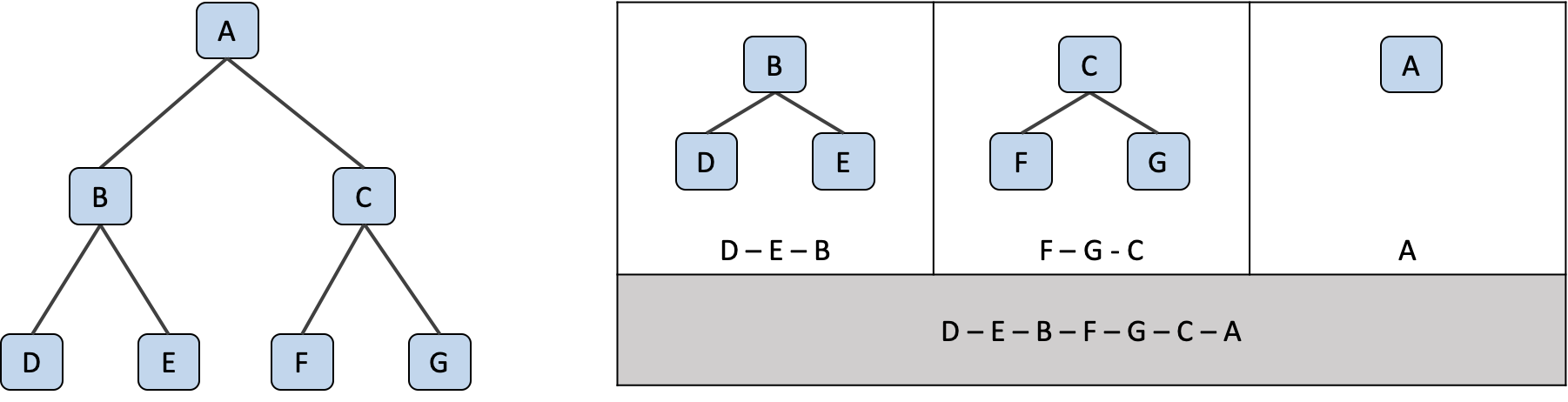
Left > Right > Root

후위 운행 의 시작은 중위 운행과 같이 가장 밑 왼쪽 노드에요. 그 다음 같은 레벨의 형제 노드가 있다면 그 형제 노드의 가장 밑 왼쪽 노드를 탐색하고 만약 형제 노드가 자식이 없는 노드면 탐색 후 부모 노드를 운행하는 과정을 반복해요.

쓰레드 이진 트리 (Thread Binary Tree)

쓰레드(Thread) 는 이진 트리의 링크 표현에서 널(NULL) 링크를 트리의 운행을 위해 트리에서 더 높은 위치의 노드들을 지시하는 포인터에요. 이러한 포인터를 사용함으로써 메모리 공간을 효율적으로 사용하고, 운행상의 효율을 기하는 트리가 바로 쓰레드 이진 트리에요. 뿐만 아니라, 널 링크를 쓰레드 시킴으로서 운행 속도가 빨라지고, 스택의 도움 없이 후속자를 찾을 수도 있어요.

일반적으로 쓰레드 이진 트리를 표현할 때는, 노드의 널 포인터가 좌측 포인터라면 그 노드 직전에 검사될 노드를 지적하도독 포인터 값을 설정하고, 반대로 우측 포인터라면 그 노드 직후에 검사될 노드를 지적하도록 포인터 값을 설정하면 돼요.

그래프 (Graph)

그래프 (Graph) 는 객체 간의 연결을 시각적으로 표현한 자료 구조에요. 다양한 것들을 표현할 수 있으며 다양한 곳에 적용되죠. 웹 페이지를 링크로 연결한 웹 사이트, 교차로를 도로로 연결한 지도, 그리고 부품을 배선으로 연결한 회로 등이 모두 그래프의 예라고 볼 수 있어요.

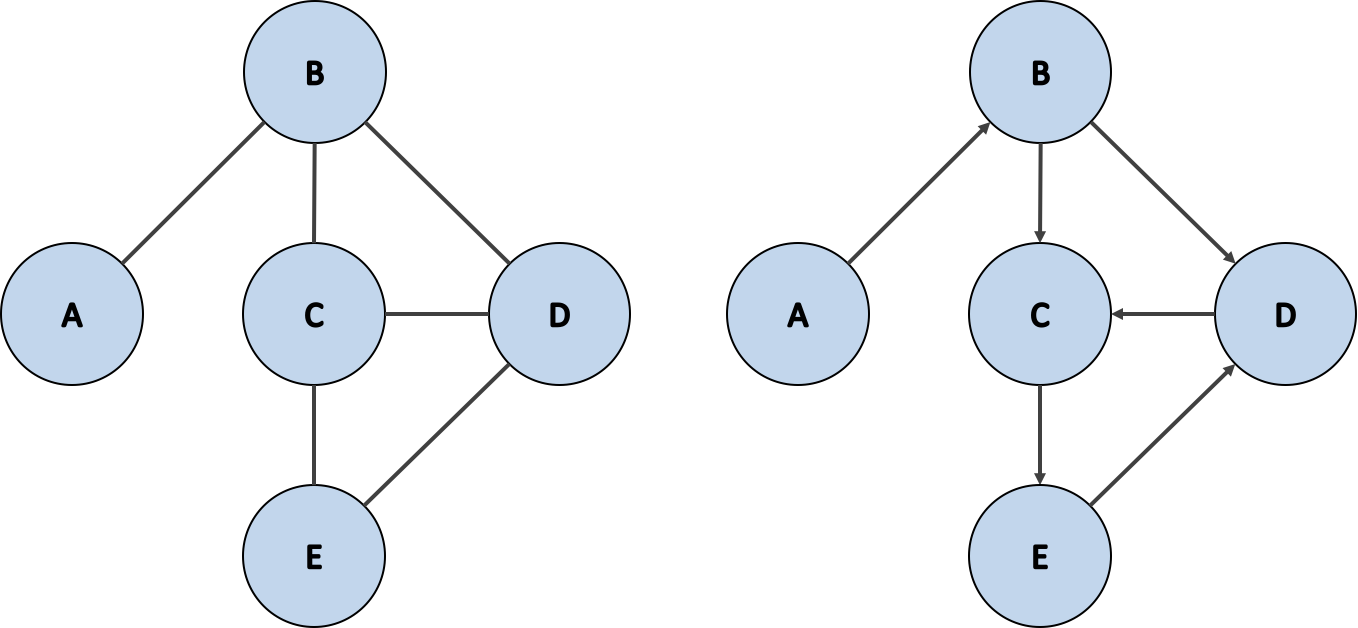
그래프는 위 그림과 같이 표현할 수 있어요. 여기서 그래프를 형성하는 각 노드들을 정점 (Vertex) 이라 하고 이 노드 간의 연결을 간선 (Edge) 라고 해요. 그리고 특정 노드에 연결된 간선의 개수를 정점 차수 (Dgree of Vertex) 라 불러요.

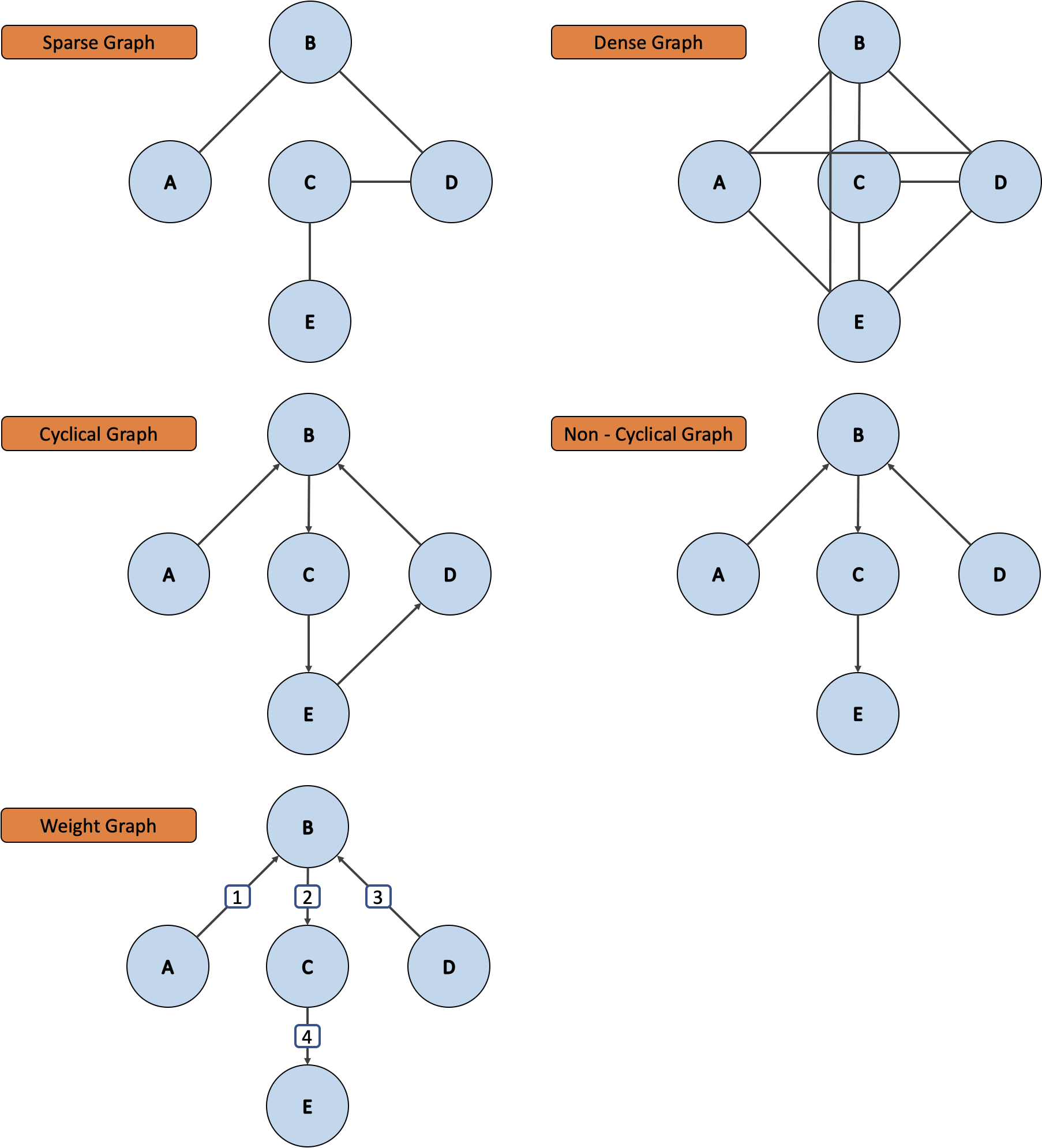
그리고 그래프에는 여러 종류가 있는데, 정점들 간에 가능한 연결 중 일부만 존재하는 경우를 희소 그래프 , 다양한 정점들 간에 연결이 많은 경우를 밀집 그래프 , 어떤 정점에서 출발해 해당 정점으로 다시 돌아오는 경우가 존재하는 순환 그래프 , 그리고 간선에 대한 값을 통해 문맥에 따라 다양한 것을 나타낼 수 있는 가중치 그래프 등이 있어요.

무지향성 그래프 (Undirected Graph)

무지향성 그래프 (Undirected Graph) 는 간선 간에 방향이 없는 그래프에요. 간선은 두 노드 간에 방향 없이 상호 연결을 암시하죠. 무지향성 그래프를 자료 구조 클래스로 표현하는 다양한 방법이 있어요. 가장 흔한 방법 두 가지로는 인접 리스트 (Adjacency List) 와 인접 행렬 (Adjacency Matrix) 가 있어요. 인접 리스트는 정점을 노드의 키로 사용하며 해당 노드의 이웃들을 리스트에 저장해요. 반면 인접 행렬은 행렬의 각 항목이 두 정점 간에 연결을 나타내는 정방행렬이에요.

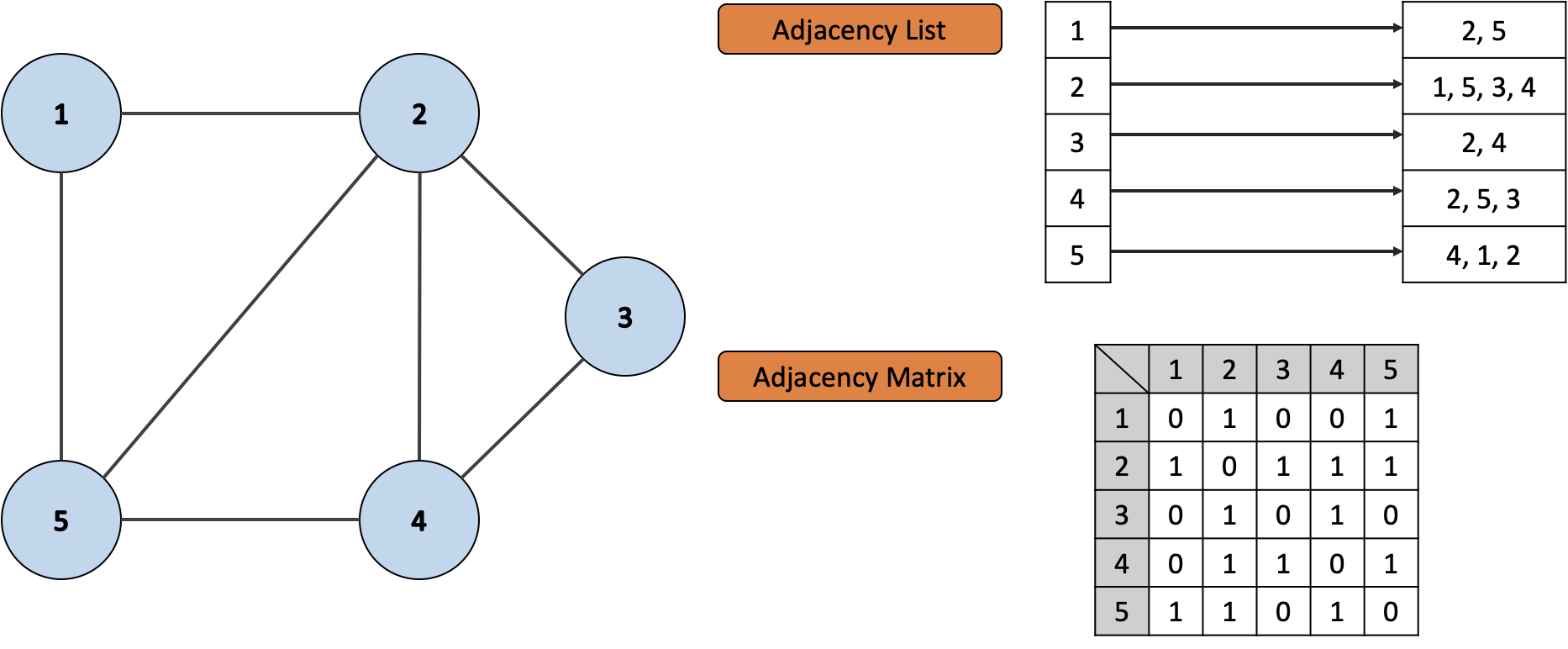
아래는 가중치가 있는 무지향성 그래프 를 생성한 뒤 인접 리스트를 이용해 정점과 간선을 추가하는 코드에요.

// Undirected Graph
function UndirectedGraph() {
  this.edges = {};
}

UndirectedGraph.prototype.addVertex = function(vertex) {
  this.edges[vertex] = {};
}

UndirectedGraph.prototype.addEdge = function(vertex1, vertex2, weight) {
  if (wight === undefined) {
    weight = 0;
  }
  this.edges[vertex1][vertex2] = weight;
  this.edges[vertex2][vertex1] = weight;
}

// Test
const graph = new UndirectedGraph();
graph.addVertex(1);
graph.addVertex(2);
graph.addEdge(1, 2, 1);
graph.addVertex(3);
graph.addVertex(4);
graph.addVertex(5);
graph.addEdge(2, 3, 8);
graph.addEdge(3, 4, 10);
graph.addEdge(4, 5, 100);
graph.addEdge(1, 5, 88);
console.log(graph.edges);

아래는 결과에 따른 콘솔값과 도표에요.

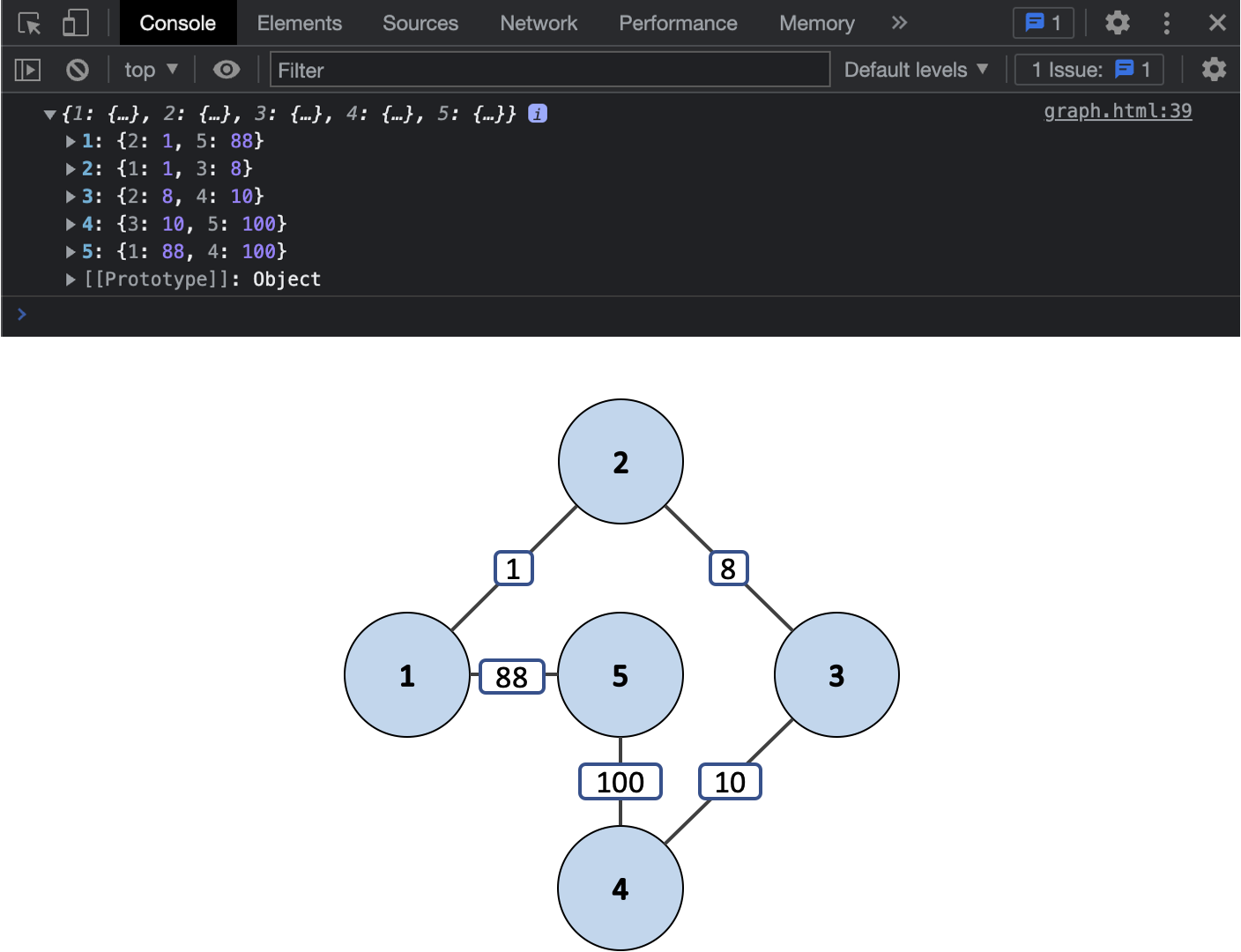
이번엔 동일한 예를 이용해 간선과 정점을 삭제하는 코드를 작성해볼게요.

// Undirected Graph
UndirectedGraph.prototype.removeEdge = function(vertex1, vertex2) {
  if (this.edges[vertex1] && this.edges[vertex1][vertex2] !== undefined) {
    delete this.edges[vertex1][vertex2];
  }
  if (this.edges[vertex2] && this.edges[vertex1][vertex2] !== undefined) {
    delete this.edges[vertex2][vertex1];
  }
};

UndirectedGraph.prototype.removeVertex = function(vertex) {
  for (let adjacentVertex in this.edges[vertex]) {
    this.removeEdge(adjacentVertex, vertex);
  }

  delete this.edges[vertex];
};

// Test
graph.removeVertex(5);
graph.removeVertex(1);
graph.removeEdge(2, 3);
console.log(graph.edges);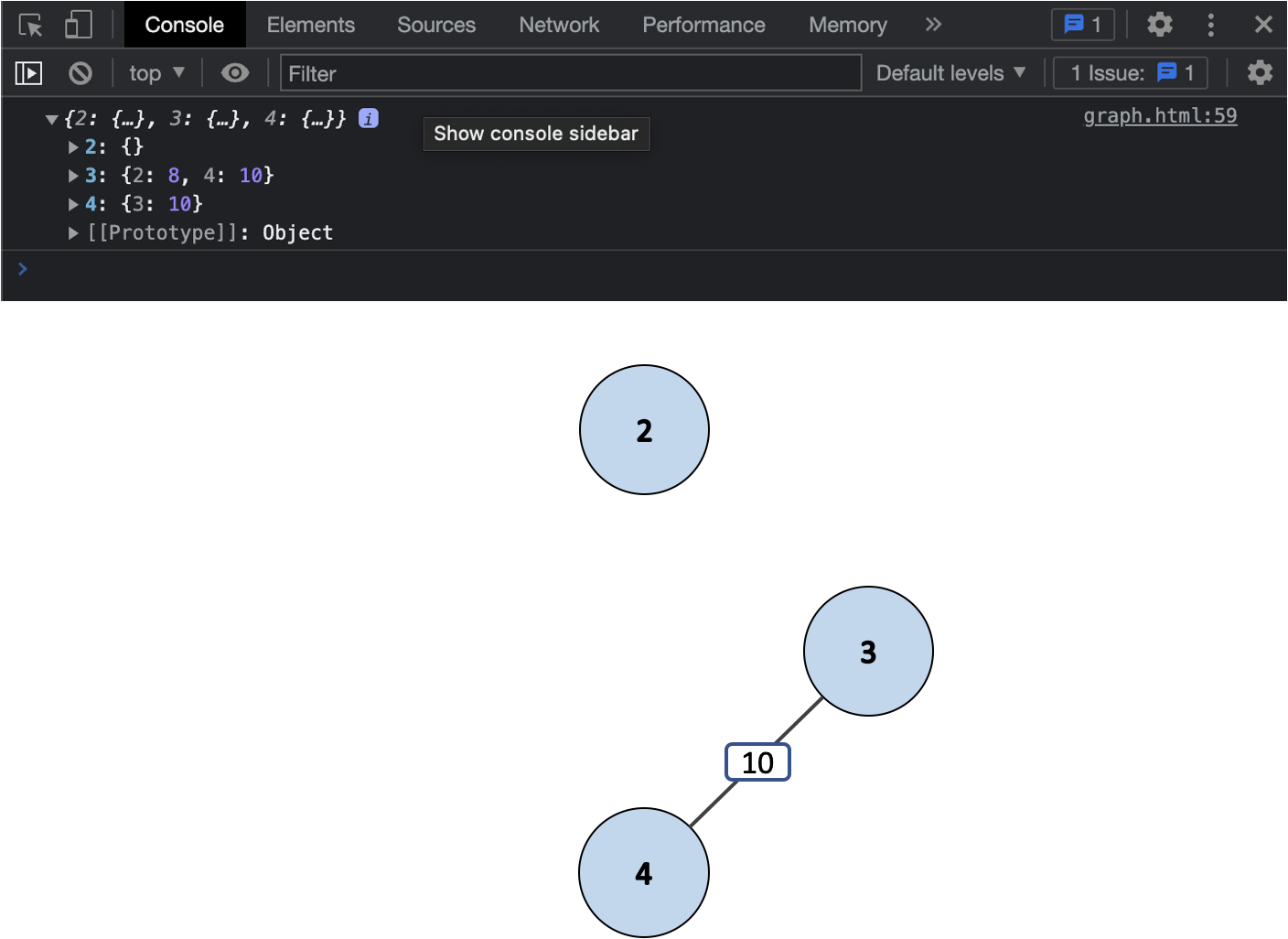

이렇게 간선과 정점들이 잘 사라진 것을 볼 수 있네요.

지향성 그래프 (Directed Graph)

지향성 그래프 (Directed Graph) 는 정점 간에 방향이 있는 그래프에요. 즉, 그래프의 각 간선은 한 정점에서 다른 정점으로 향하죠. 지향성 그래프 역시 무지향성 그래프처럼 인접 리스트 를 이용해 구현할 수 있어요. 아래는 이를 구현한 코드에요.

// Directed Graph
function DirectedGraph() {
  this.edges = {};
};

DirectedGraph.prototype.addVertex = function(vertex) {
  this.edges[vertex] = {};
};

DirectedGraph.prototype.addEdge = function(origVertex, destVertex, weight) {
  if (weight === undefined) {
    weight = 0;
  }
  this.edges[origVertex][destVertex] = weight;
};

// Test
const graph = new DirectedGraph();
graph.addVertex('A');
graph.addVertex('B');
graph.addVertex('C');
graph.addEdge('A', 'B', 1);
graph.addEdge('B', 'C', 2);
graph.addEdge('C', 'A', 3);
console.log(graph.edges);

그리고 코드를 통한 결과값과 그에 대한 도표에요.

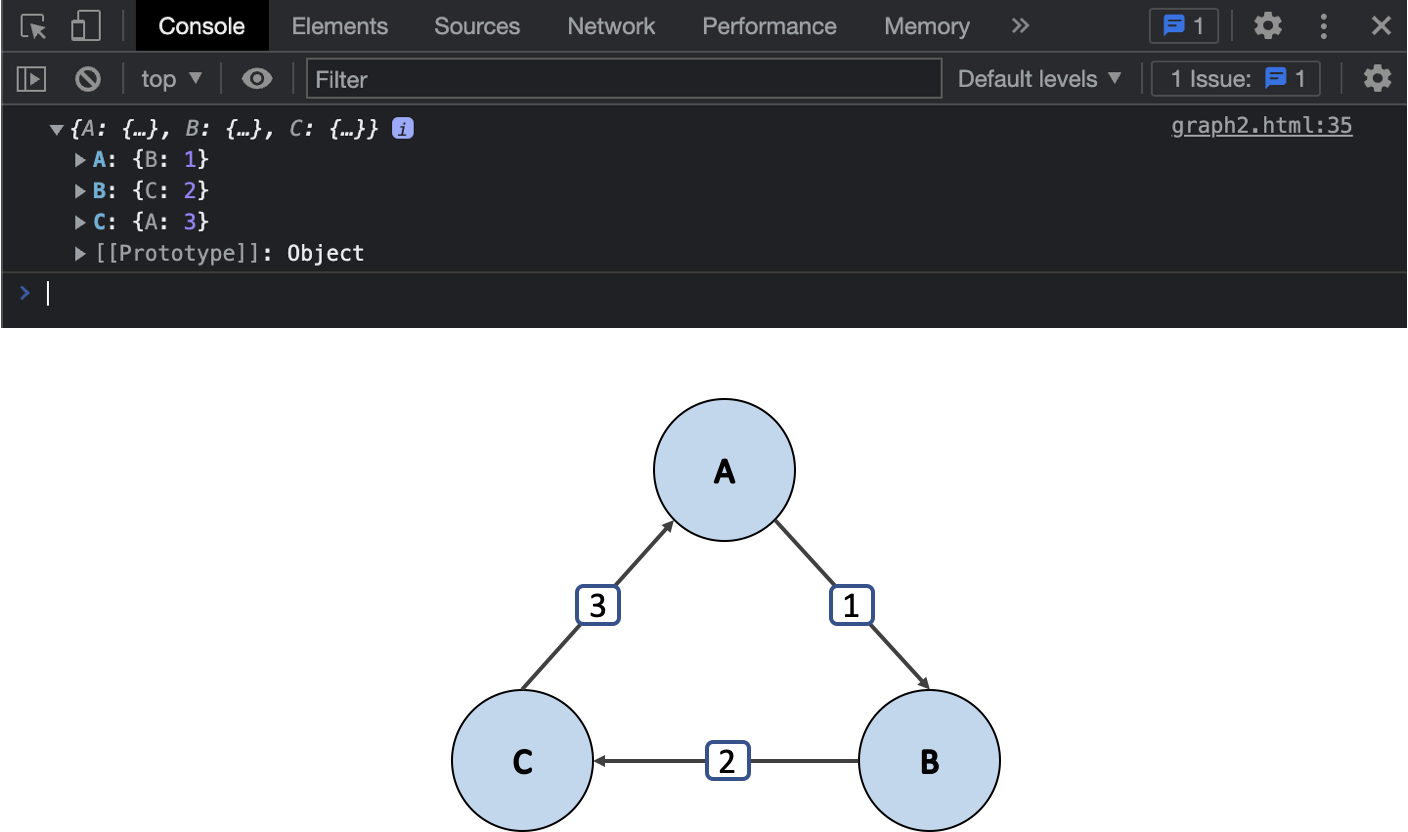
지향성 그래프의 삭제 구현도 무지향성 그래프와 거의 유사하지만, 원점이 되는 정점만을 삭제해야 한다는 점이 달라요.

// Directed Graph
DirectedGraph.prototype.removeEdge = function(origVertex, destVertex) {
  if (this.edges[origVertex] && this.edges[origVertex][destVertex] !== undefined) {
    delete this.edges[origVertex][destVertex];
  }
};

DirectedGraph.prototype.removeVertex = function(vertex) {
  for (let adjacentVertex in this.edges) {
    if (this.edges[adjacentVertex].hasOwnProperty(vertex)) {
      this.removeEdge(adjacentVertex, vertex);
    }
  }

  delete this.edges[vertex];
};

// Test
graph.removeVertex('A');
graph.removeEdge('B', 'C');
console.log(graph.edges);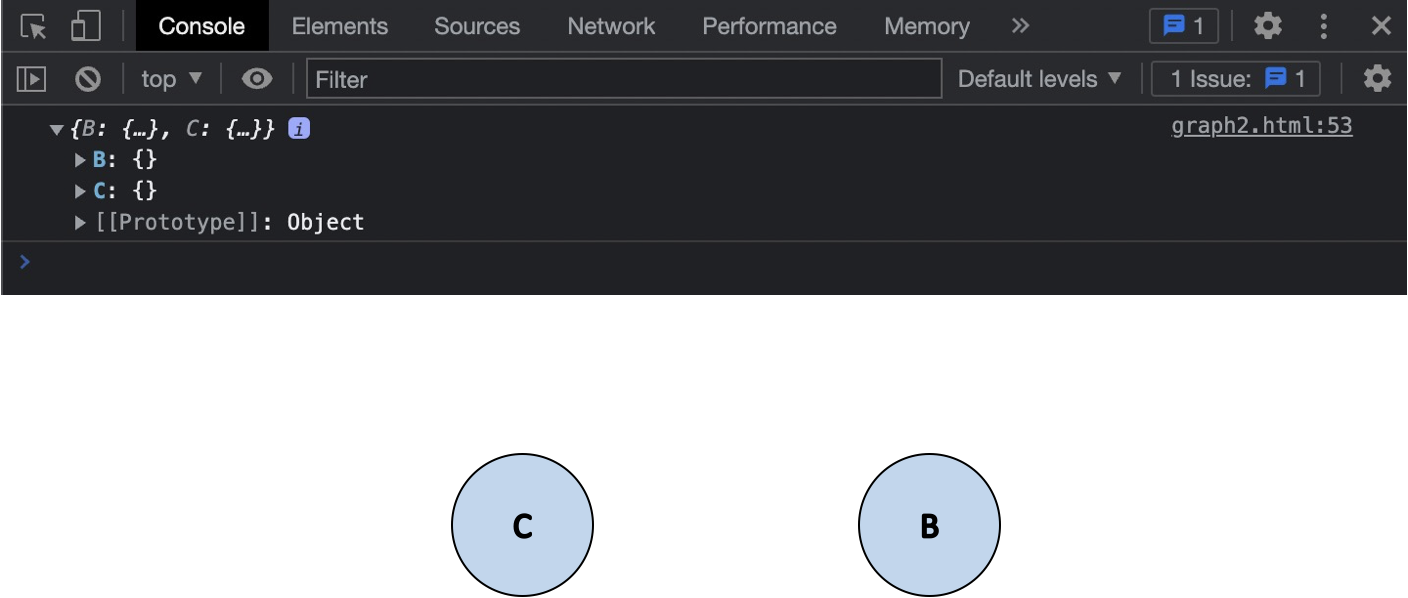

이렇게 지향성 그래프 와 무지향성 그래프 모두 인접 리스트 를 활용하여 쉽게 구현할 수 있어요.

그래프 순회

그래프를 순회하는 방법은 다양해요. 그 중에서 가장 일반적인 방법으로 너비 우선 검색 과 깊이 우선 검색 이 있습니다.

너비 우선 검색 (BFS: Breath First Search)

너비 우선 검색 (BFS: Breath First Search) 은 그래프에서 연결된 노드와 해당 노드들 간의 간선을 순서대로 검색하는 알고리즘이에요.

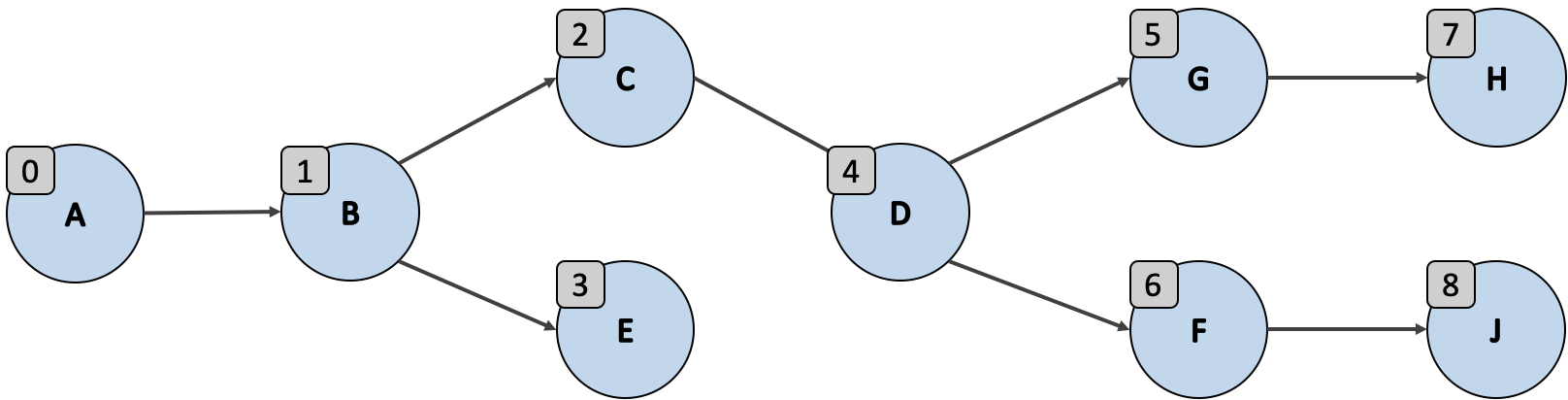
위의 지향성 그래프를 통해 너비 우선 검색의 과정을 살펴봐요. 우선 너비 우선 검색은 큐 를 필요로해요. 각 노드에 연결된 각 정점을 큐에 추가한 다음 큐의 각 항목을 방문하죠.

다음은 앞서 작성한 지향성 그래프 클래스를 활용해 구현한 코드에요.

// BFS
DirectedGraph.prototype.traverseBFS = function(vertex, fn) {
  const queue = [], visited = {};

  queue.push(vertex);

  while (queue.length) {
    vertex = queue.shift();
    if (!visited[vertex]) {
      visited[vertex] = true;
      fn(vertex);
      for (let adjacentVertex in this.edges[vertex]) {
        queue.push(adjacentVertex);
      }
    }
  }
}

// Test
const graph = new DirectedGraph();
graph.addVertex('A');
graph.addVertex('B');
graph.addVertex('C');
graph.addVertex('D');
graph.addVertex('E');
graph.addVertex('F');
graph.addVertex('G');
graph.addVertex('H');
graph.addVertex('J');
graph.addEdge('A', 'B');
graph.addEdge('B', 'C');
graph.addEdge('B', 'E');
graph.addEdge('C', 'D');
graph.addEdge('D', 'G');
graph.addEdge('D', 'F');
graph.addEdge('G', 'H');
graph.addEdge('F', 'J');
graph.traverseBFS('B', vertex => console.log(vertex));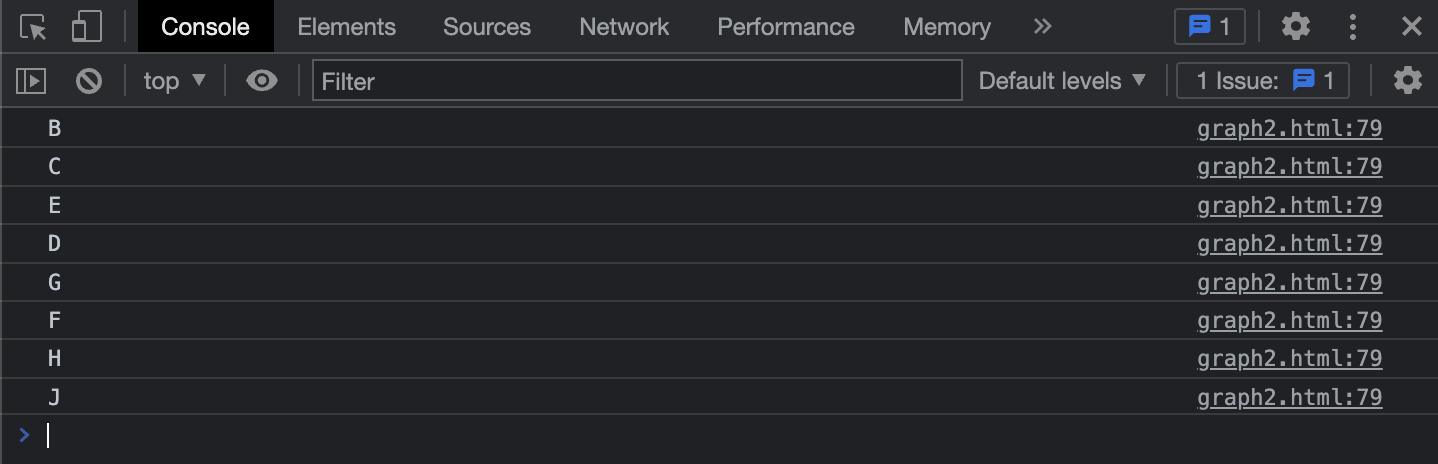

위 그림에 나온 순서처럼 너비 우선 검색이 제대로 구현된 걸 볼 수 있어요.

깊이 우선 검색 (DFS: Depth First Search)

깊이 우선 검색 (DFS: Depth First Search) 은 그래프에서 다른 연결을 방문하기 전에 하나의 연결을 깊게 파고들며 순회하는 검색 알고리즘이에요.

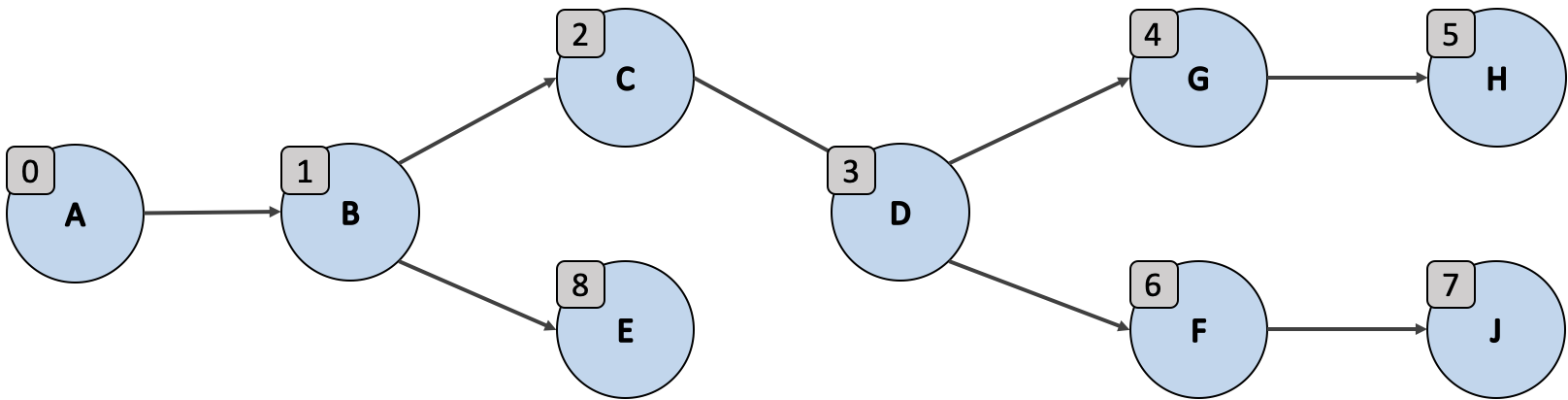
깊이 우선 검색은 위에서 보듯이 노드 E를 가장 마지막에 방훈하는데에 주목해야 해요. 이는 깊이 우선 검색이 노드 E를 방문하기 전에 노드 C와 깊이쪽으로 연결된 모든 노드를 방문하기 때문이죠. 여기서는 특정 노드의 깊이쪽으로 연결된 모든 겅로를 탐색하기 위해 재귀를 사용해 구현할거에요.

// DFS
DirectedGraph.prototype.traverseDFS = function(vertex, fn) {
  const visited = {};
  this.helpTraverseDFS(vertex, visited, fn);
};

DirectedGraph.prototype.helpTraverseDFS = function(vertex, visited, fn) {
  visited[vertex] = true;
  fn(vertex);
  for (let adjacentVertex in this.edges[vertex]) {
    if (!visited[adjacentVertex]) {
      this.helpTraverseDFS(adjacentVertex, visited, fn);
    }
  }
};

// Test
const graph = new DirectedGraph();
graph.addVertex('A');
graph.addVertex('B');
graph.addVertex('C');
graph.addVertex('D');
graph.addVertex('E');
graph.addVertex('F');
graph.addVertex('G');
graph.addVertex('H');
graph.addVertex('J');
graph.addEdge('A', 'B');
graph.addEdge('B', 'C');
graph.addEdge('B', 'E');
graph.addEdge('C', 'D');
graph.addEdge('D', 'G');
graph.addEdge('D', 'F');
graph.addEdge('G', 'H');
graph.addEdge('F', 'J');
graph.traverseDFS('B', vertex => console.log(vertex));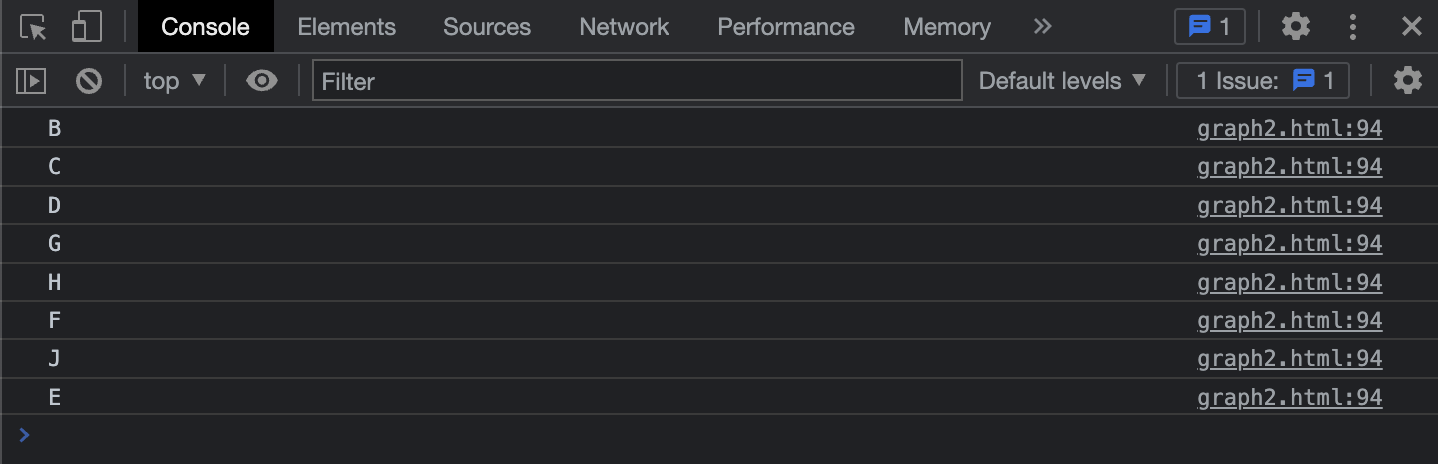

그림에서 봤던 순서대로 깊이 우선 탐색이 잘 구현 되었네요.

다익스트라 알고리즘 (Dijkstra's Algorithm)

앞선 알고리즘들은 간선이 가진 가중치와 상관없이 탐색하는 방법들이었어요. 그렇다면 가중치 가 존재하는 그래프에서는 과연 어떻게 탐색해야 할까요.

가중치가 있는 그래프에서 가장 중요한 질문은 특정 노드에서 다른 노드까지의 가장 짧은 경로가 무엇인지에요. 그리고 이를 알아내는 알고리즘 중 하나가 바로 다익스트라의 알고리즘이에요.

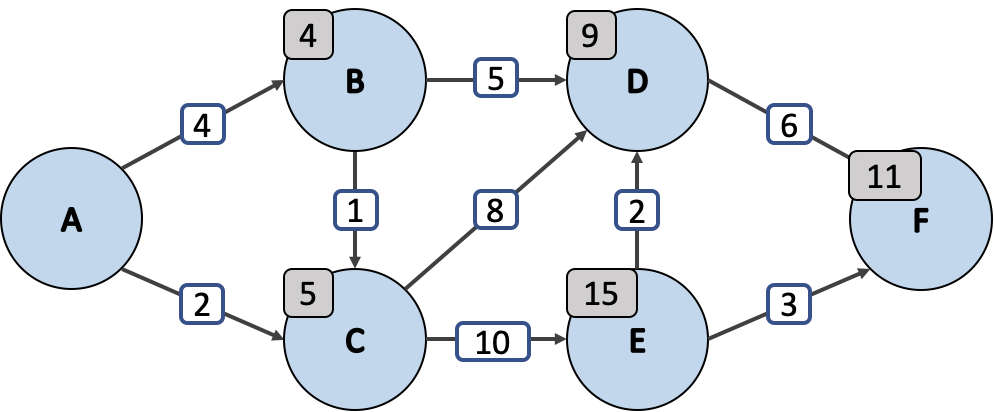
다익스트라의 알고리즘 (Dijkstra's Algorithm) 은 목적지에 도달하기 위해 반복 루프를 활용하여 각 단계에서 최단 경로를 취하는 방식으로 동작해요. 위 그림과 같은 가중치가 있는 지향성 그래프를 통해 알고리즘을 구현해볼게요.

// Dijkstra's Algorithm
function isEmpty(obj) {
  return Object.keys(obj).length === 0;
}

function extractMin(Q, dist) {
  let minimumDistance = Infinity, nodeWithMinimumDistance = null;

  for (let node in Q) {
    if (dist[node] <= minimumDistance) {
      minimumDistance = dist[node];
      nodeWithMinimumDistance = node;
    }
  }

  return nodeWithMinimumDistance;
}

DirectedGraph.prototype.dijkstra = function(source) {
  const Q = {}, dist = {};

  for (let vertex in this.edges) {
    dist[vertex] = Infinity;
    Q[vertex] = this.edges[vertex];
  }
  dist[source] = 0;

  while (!isEmpty(Q)) { 
    let u = extractMin(Q, dist);

    delete Q[u];

    for (let neighbor in this.edges[u]) {
      const alt = dist[u] + this.edges[u][neighbor];
      if (alt < dist[neighbor]) {
        dist[neighbor] = alt;
      }
    }
  }

  return dist;
}

// Test
const graph = new DirectedGraph();
graph.addVertex('A');
graph.addVertex('B');
graph.addVertex('C');
graph.addVertex('D');
graph.addVertex('E');
graph.addVertex('F');
graph.addEdge('A', 'B', 4);
graph.addEdge('A', 'C', 8);
graph.addEdge('B', 'C', 1);
graph.addEdge('B', 'D', 5);
graph.addEdge('C', 'D', 8);
graph.addEdge('C', 'E', 10);
graph.addEdge('D', 'F', 2);
graph.addEdge('E', 'D', 2);
graph.addEdge('E', 'F', 3);
console.log(graph.dijkstra('A'));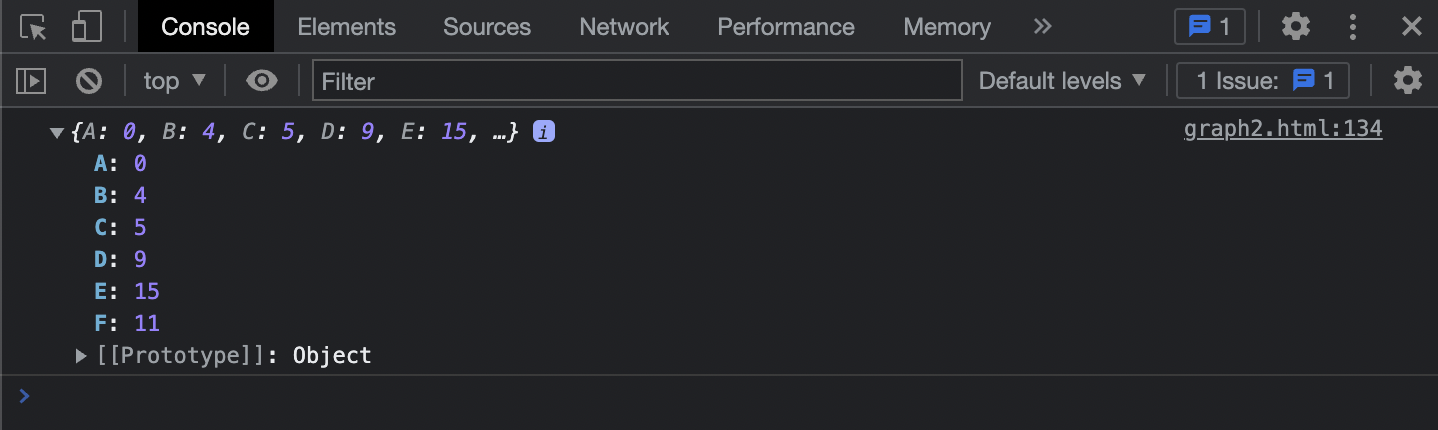

이렇게 각 노드별 소스로부터의 최단 거리가 잘 나타난 것을 확인할 수 있어요.

정렬

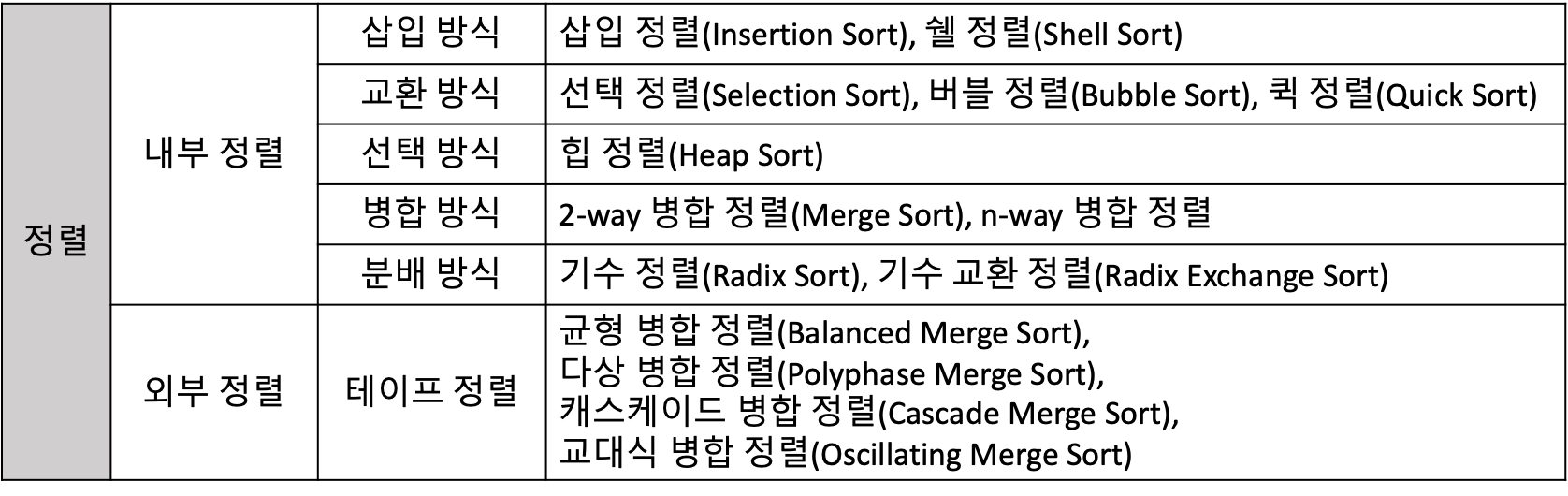
정렬 은 주어진 자료 원소를 순서화 기준에 따라 재배열하는 연산을 뜻해요. 정렬 장소에 따라 내부 정렬(주기억 장치)과 외부 정렬(보조 기억 장치)로 나뉘어요.

선택 정렬 (Selction Sort)

선택 정렬 은 가장 단순한 작업 방식 중 하나로, 버블 정렬이나 삽입 정렬보다 이동 횟수를 줄일 수 있어요. 오름차순 정렬일 경우, 처음 자료부터 시작하여 자료들 중 가장 작은 값을 처음 자료의 위치와 교환하는 작업을 계속 반복하면 됩답니다. 이 때, 알고리즘의 전체 메모리 비교 횟수는 n(n-1)/2 에요.

선택 정렬 과정
1회전 : n개의 레코드로부터 최솟값을 찾아 첫번 레코드 위치에 놓는다.
2회전 : n-1개 중 최솟값을 찾아 두번째 위치에 놓는다.
n-1회전 : n-1번째와 n번째 레코드 중 키 값이 작은 레코드를 n-1번째에 놓는다.

// Selection Sort
const selectionSort = arr => {
  const len = arr.length;

  for (let i = 0; i < len - 1; i ++) {
    let currentMin = i;
    for (let j = i + 1; j < len; j ++) {
      if (arr[j] < arr[currentMin]) currentMin = j;
    }

    if (currentMin !== i) {
      // Swap the values
      [arr[i], arr[currentMin]] = [arr[currentMin], arr[i]];
    }
  }

  return arr;
}

// Test
const getRandomInt = (min, max) => {
  return Math.floor(Math.random() * (max - min + 1)) + min;
}
const arr = [];
for (let i = 0; i < 10; i ++) { // 비정렬 무작위 수열 생성
  arr.push(getRandomInt(1, 100));
}

console.log(arr); // 무작위 배열
const sortedArr = selectionSort(arr);
console.log(sortedArr); // 정렬된 배열

삽입 정렬 (Insertion Sort)

삽입 정렬 은 알고리즘 진행시에 이전 단계의 정렬된 서브 파일에 레코드의 순서를 찾아 하나씩 입력시키는 정렬방법이에요. 이 때, 알고리즘의 전체 메모리 비교 횟수는 n(n-1)/2 에요.

삽입 정렬 과정
1회전 : 2번째 키와 1번째 키를 비교 순서대로 나열
2회전 : 3번째 키를 1번째 키와 2번째 키와 비교 순서대로 나열
n-1회전 : n번째 키를 n-1개의 키와 비교하여 알맞은 순서에 삽입

// Insertion Sort
const insertionSort = arr => {
  const len = arr.length;

  for (let i = 1; i < len; i++) {
    currentValue = arr[i];
    let j = i - 1;
    while (j >= 0 && arr[j] > currentValue) {
      arr[j + 1] = arr[j];
      j--;
    }

    arr[j + 1] = currentValue;
  }

  return arr;
}

// Test
const getRandomInt = (min, max) => {
  return Math.floor(Math.random() * (max - min + 1)) + min;
}
const arr = [];
for (let i = 0; i < 10; i ++) { // 비정렬 무작위 수열 생성
  arr.push(getRandomInt(1, 100));
}

console.log(arr); // 무작위 배열
const sortedArr = insertionSort(arr);
console.log(sortedArr); // 정렬된 배열

거품 정렬 (Bubble Sort)

거품 정렬 은 메모리에 인접한 2개의 자료를 비교하여 크기에 따라 상호 메모리 위치를 교환하는 방법으로 정렬해요. 이 때, 알고리즘의 전체 메모리 비교 횟수는 n(n-1)/2 입니다. 시간 복잡도가 큰 만큼 거품 정렬은 최악의 정렬 중 하나에요.

거품 정렬 과정
1회전 : 1번째와 2번째, 2번째와 3번째, ... , n-1번째와 n번째 레코드 키 값을 비교하여 가장 큰 값의 원소가 제일 마지막에 위치한다.
2회전 : 마지막 레코드를 제외하고 1번째부터 n-1번째 레코드를 비교하여 두번째로 큰 값의 원소가 n-1번째에 위치한다.
n-1회전 : 1번째와 2번째 레코드의 키 값을 비교한다.

// Bubble Sort
const bubbleSort = arr => {
  const len = arr.length;

  for (let i = 0; i < len - 1; i++) {
    for (let j = 0; j < len - i - 1; j++) {
      if (arr[j] > arr[j + 1]) {
        [arr[j], arr[j + 1]] = [arr[j + 1], arr[j]];
      }
    }
  }

  return arr;
}

// Test
const getRandomInt = (min, max) => {
  return Math.floor(Math.random() * (max - min + 1)) + min;
}
const arr = [];
for (let i = 0; i < 10; i ++) { // 비정렬 무작위 수열 생성
  arr.push(getRandomInt(1, 100));
}

console.log(arr); // 무작위 배열
const sortedArr = bubbleSort(arr);
console.log(sortedArr); // 정렬된 배열

쉘 정렬 (Shell Sort)

쉘 정렬 은 버블 정렬의 메모리 위치교환 횟수를 최소화하기 위한 방법으로 메모리 위치가 먼 원소끼리 교환하도록 하는 정렬이에요. 먼저 입력 파일을 정의된 매개변수에 따라 서브 파일을 구성하고 각 서브 파일을 삽입 정렬 방식으로 정렬하는 과정을 반복해서 구현합니다.

쉘 정렬 과정
1회전 : 매개변수 h=3일 때, 1, 4, 7, 10번째 레코드가 부분 리스트를 구성, 2, 5, 8, 11번째 레코드가 부분 리스트를 구성, 3, 6, 9, 1번째 레코드가 부분 리스트를 구성, 각 부분 리스트마다 정렬한다.
2회전 : 매개변수를 h=2로 하여 첫번째 과정을 반복한다.
3회전 : 매개변수를 h=1로 하여 첫번쨰 과정을 반복한다.

빠른 정렬 (Quick Sort)

빠른 정렬 은 리스트의 중간 원소를 선택해서 피벗(Pivot)으로 설정하고 피벗을 기준으로 피벗보다 작은 원소들은 피벗 앞으로 피벗보다 큰 원소들은 피벗의 뒤로 가도록 리스트를 둘로 나누어요. 리스트를 둘로 나누는 것을 분할이라고 하며 분할 이후에 피벗은 더 이상 움직이지 않게 됩니다. 이제 분할된 두 개의 작은 리스트에 대해 재귀적으로 이 과정을 리스트의 크기가 0이나 1이 될 때까지 반복하면 돼요.

// Quick Sort
const quickSort = list => {
  let len = list.length, pivot = list[0], left = [], right = [];
  if (len < 2) return list;

  for (let i = 1; i < len; i++) {
    switch (true) {
      case (list[i] < pivot):
        left.push(list[i]);
        break;
      case (list[i] >= pivot):
        if (list[i]) right.push(list[i]);
        break;
    }
  }

  return [...(quickSort(left), pivot, ...quickSort(right)];
};

// Test
const getRandomInt = (min, max) => {
  return Math.floor(Math.random() * (max - min + 1)) + min;
}
const arr = [];
for (let i = 0; i < 10; i ++) { // 비정렬 무작위 수열 생성
  arr.push(getRandomInt(1, 100));
}

console.log(arr); // 무작위 배열
const sortedArr = quickSort(arr);
console.log(sortedArr); // 정렬된 배열

병합 정렬 (Merge Sort)

병합 정렬 은 각 하위 배열에 하나의 항목이 존재할 때까지 배열을 하위 배열로 나눠요, 그러고 나서 각 하위 배열을 정렬된 순서로 병합해요. 밑에 코드의 병합 정렬 함수는 큰 배열을 두 개의 개별적인 배열로 반할한 다음 재귀적으로 문제를 해결해요. 병합 정렬은 n개의 배열을 생성하기 때문에 공간 복잡도가 큰 편이에요. 그래도 장점이라고 한다면 시간 복잡도가 보장이 되는 안정적인 정렬이랍니다.

// Merge Sort
const mergeSort = arr => {
  const merge = (left, right) => {
    let results = [], li = 0, ri = 0;

    while (li < left.length && ri < right.length) {
      if (left[li] < right[ri]) {
        results.push(left[li++]);
      } else {
        results.push(right[ri++]);
      }
    }

    const lRemains = left.slice(li), rRemains = right.slice(ri);

    return [...results, ...lRemains, ...rRemains];
  };

  if (arr.length < 2) return arr;

  const mid = Math.floor(arr.length / 2), leftArr = arr.slice(0, mid), rightArr = arr.slice(mid);

  return merge(mergeSort(leftArr), mergeSort(rightArr));
}

// Test
const getRandomInt = (min, max) => {
  return Math.floor(Math.random() * (max - min + 1)) + min;
}
const arr1 = [], arr2 = [];
for (let i = 0; i < 10; i ++) { // 비정렬 무작위 수열 생성
  arr1.push(getRandomInt(1, 100));
  arr2.push(getRandomInt(1, 100));
}

console.log(arr1.sort((a, b) => a - b));
console.log(arr2.sort((a, b) => a - b)); 
const sortedArr = mergeSort(arr1, arr2);
console.log(sortedArr); // 합병된 배열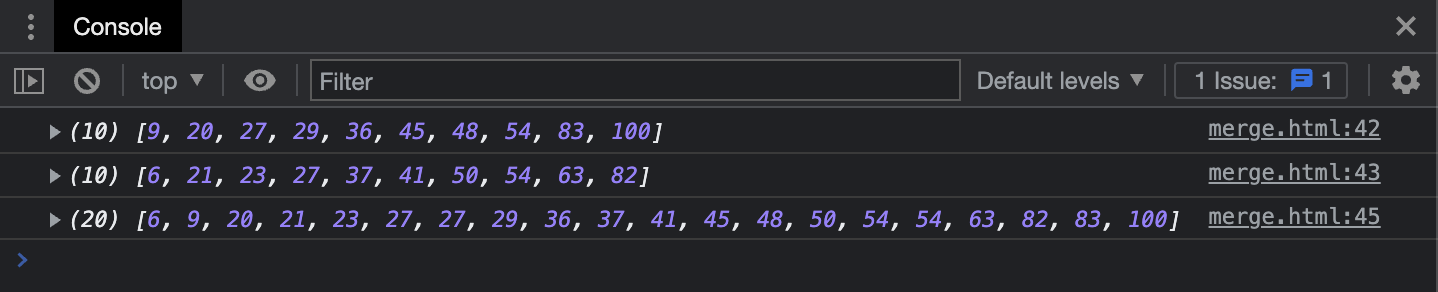

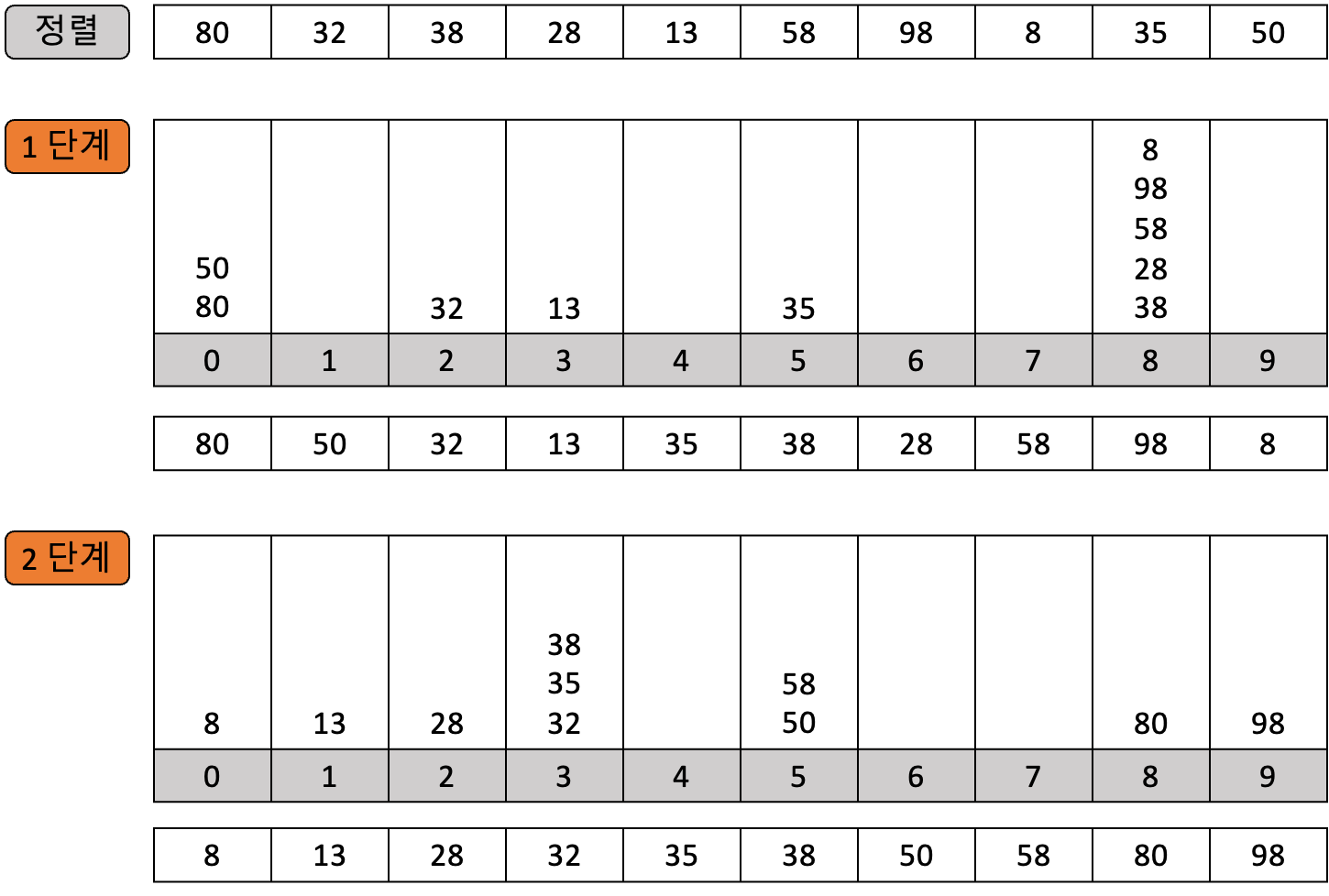
분배에 의한 정렬

분배 를 통한 정렬은 키를 구성하고 있는 각 자릿수(십자리, 일자리)별로 버켓에 분배하여 정렬하는 방식입니다. 먼저 특정한 자릿수를 기준으로 버켓을 채우고 다시 다른 자릿수를 기준으로 재배열하는 과정을 반복하여 자료를 정렬하면 돼요. 여기에는 최하위 자릿수를 중시하는 LSD(Least Signification Digital) 방법과 최상위 자릿수를 중시하는 MSD(Most Signification Digital) 방법 두 가지가 있어요.

// Radix Sort
const radixSort = arr => {
  const maxDigit = getMaxDigitLen(arr);

  for (let i = 1; i <= maxDigit; i++) {
    const digitBuckets = [];

    for (let j = 0; j < arr.length; j++) {
      const digit = getDigit(arr[j], i);
      digitBuckets[digit] = digitBuckets[digit] || [];
      digitBuckets[digit].push(arr[j]);
    }

    let index = 0;
    for (let j = 0; j < digitBuckets.length; j++) {
      if (digitBuckets[j] && digitBuckets[j].length > 0) {
        for (let k = 0; k < digitBuckets[j].length; k++) {
          arr[index++] = digitBuckets[j][k];
        }
      }
    }
  }

  return arr;
};

const getDigit = (num, position) => {
  if (num.toString().length < position) return 0;

  const radixPosition = Math.pow(10, position - 1);
  const digit = (Math.floor(num / radixPosition)) % 10;

  return digit
};

const getMaxDigitLen = arr => {
  const maxVal = Math.max.apply(Math, arr);

  return Math.ceil(Math.log10(maxVal));
};

// Test
const getRandomInt = (min, max) => {
  return Math.floor(Math.random() * (max - min + 1)) + min;
}
const arr = [];
for (let i = 0; i < 10; i ++) { // 비정렬 무작위 수열 생성
  arr.push(getRandomInt(1, 100));
}

console.log(arr); // 무작위 배열
const sortedArr = radixSort(arr);
console.log(sortedArr); // 정렬된 배열

검색

정렬 과 함께 검색 은 자료구조의 근간이 되는 알고리즘이에요. 검색은 자료를 얻기 위해 자료 구조의 항목들을 반복적으로 접근하는 것을 말해요. 배열에서 검색을 수행할 때 배열이 정렬됐는지 여부에 따라 선형 검색 과 이진 검색 , 두 가지 주요 기법으로 나뉘어요. 선형 검색은 정렬된 자료와 정렬되지 않는 자료 모두에 사용가능하고, 이진 검색은 정렬된 자료에 대해 사용해요. 때문에, 선형 검색이 더 유연하지만 시간 복잡도는 더 높죠.

선형 검색

선형 검색 (Linear Search) 은 배열의 각 항목을 한 인데스씩 순차적으로 접근하면서 동작해요. 따라서 시간 복잡도는 O(n)이죠. 이와 같은 선형 검색은 배열의 정렬 여부와 상관없이 동작하기 때문에 배열이 정렬되지 않은 경우에 사용하면 좋아요. 하지만 정렬된 경우라면 검색이 더 느려지니 이진 검색을 사용하는 것이 낫답니다.

// Linear Search
const linearSearch = (array, n) => {
  for (let i = 0; i < array.length; i++) {
    if (array[i] === n) return true;
  }
  
  return false;
}

// Test
console.log(linearSearch([1, 2, 3, 4, 5, 6, 7, 8, 9], 6); // true
console.log(linearSearch([1, 2, 3, 4, 5, 6, 7, 8, 9], 10); // false

이진 검색

이진 검색 (Binary Search) 은 정렬된 자료에 사용할 수 있는 검색 알고리즘이에요. 선형 검색과는 달리 이진 검색은 중간 값을 확인해 원하는 값보다 해당 중간 값이 큰지 작은지 확인해요. 그리고 원하는 값과 중간 값의 관계에 따라 검색 방향을 결정하죠. 이진 검색은 빠르지만 배열이 정렬된 경우에만 사용할 수 있어요.

// Binary Search
const binarySearch = (array, n) => {
  let low = 0, high = array.length - 1;
  
  while (low <= high) {
    const mid = Math.floor((low + high) / 2);
    if (array[mid] === n) {
      return true;
    } else if (n > array[mid]) {
      low = mid;
    } else {
      high = mid;
    }
  }
  
  return false;
}

console.log(binarySearch([1, 2, 3, 4], 4); // true
console.log(binarySearch([1, 2, 3, 4], 5); // false

---

참고 자료

1. 오주영, 『(Javascript로 배우는) 자료구조』, 에듀컨텐츠휴피아(2019)
2. 배세민, 『자바스크립트로 하는 자료 구조와 알고리즘 : 핵심 자료구조 및 알고리즘을 이해하고 구현하기 위한 입문서』, 에이콘(2019)