안하면 찝찝한 알고리즘!
알고리즘 문제 링크
https://programmers.co.kr/learn/courses/30/lessons/81302
문제
거리두기 확인하기
문제 설명
개발자를 희망하는 죠르디가 카카오에 면접을 보러 왔습니다.
코로나 바이러스 감염 예방을 위해 응시자들은 거리를 둬서 대기를 해야하는데 개발 직군 면접인 만큼
아래와 같은 규칙으로 대기실에 거리를 두고 앉도록 안내하고 있습니다.
1. 대기실은 5개이며, 각 대기실은 5x5 크기입니다.
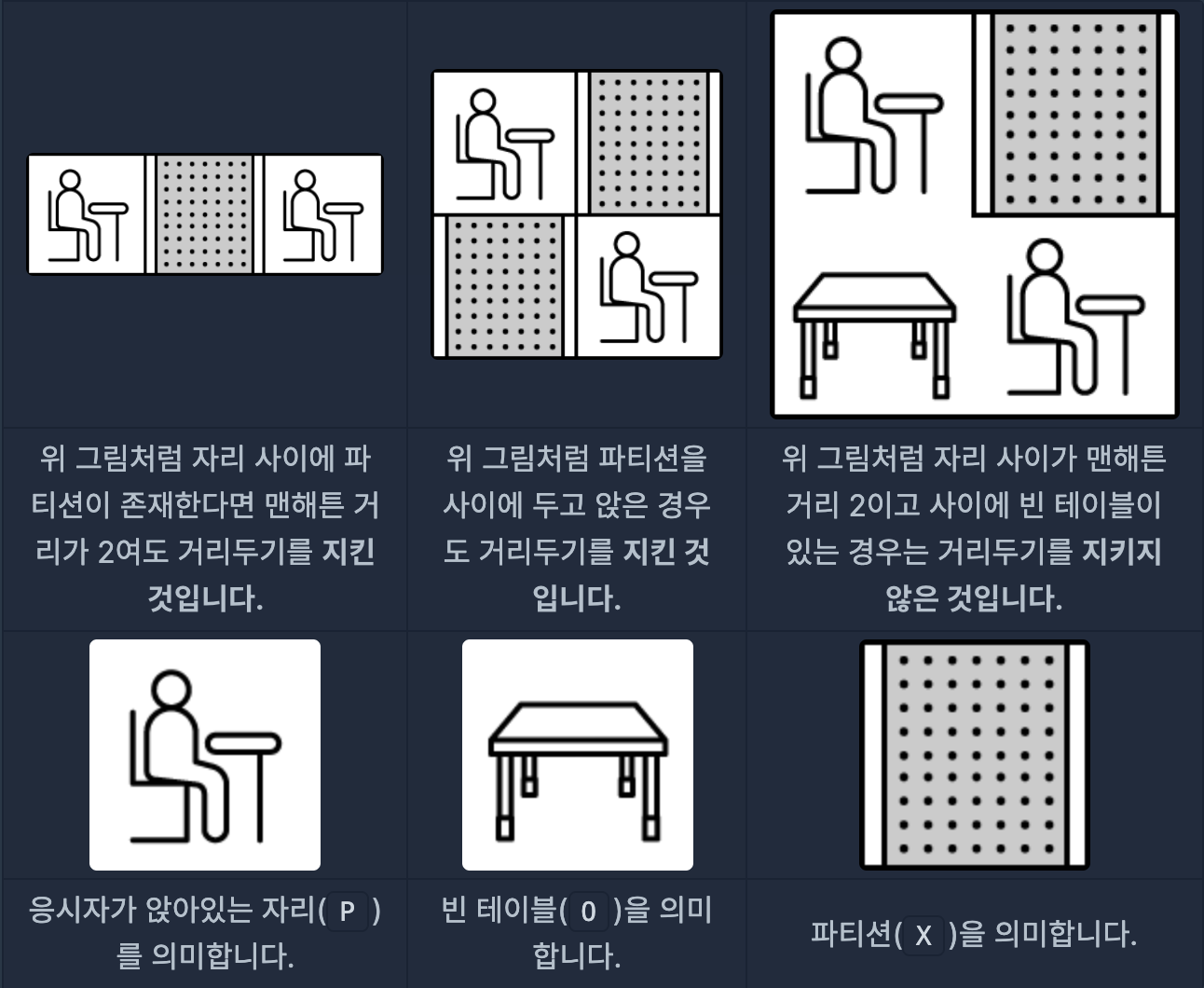
2. 거리두기를 위하여 응시자들 끼리는 맨해튼 거리1가 2 이하로 앉지 말아 주세요.
3. 단 응시자가 앉아있는 자리 사이가 파티션으로 막혀 있을 경우에는 허용합니다.
예시 이미지는 아래 있다.
5개의 대기실을 본 죠르디는 각 대기실에서 응시자들이 거리두기를 잘 기키고 있는지 알고 싶어졌습니다.
자리에 앉아있는 응시자들의 정보와 대기실 구조를 대기실별로 담은 2차원 문자열 배열 places가 매개변수로 주어집니다.
각 대기실별로 거리두기를 지키고 있으면 1을,
한 명이라도 지키지 않고 있으면 0을 배열에 담아 return 하도록 solution 함수를 완성해 주세요.
제한사항
- places의 행 길이(대기실 개수) = 5
- places의 각 행은 하나의 대기실 구조를 나타냅니다.
- places의 열 길이(대기실 세로 길이) = 5
- places의 원소는 P,O,X로 이루어진 문자열입니다.
- places 원소의 길이(대기실 가로 길이) = 5
- P는 응시자가 앉아있는 자리를 의미합니다.
- O는 빈 테이블을 의미합니다.
- X는 파티션을 의미합니다.
- 입력으로 주어지는 5개 대기실의 크기는 모두 5x5 입니다.
- return 값 형식
- 1차원 정수 배열에 5개의 원소를 담아서 return 합니다.
- places에 담겨 있는 5개 대기실의 순서대로, 거리두기 준수 여부를 차례대로 배열에 담습니다.
- 각 대기실 별로 모든 응시자가 거리두기를 지키고 있으면 1을, 한 명이라도 지키지 않고 있으면 0을 담습니다.
입출력 예
places
[["POOOP", "OXXOX", "OPXPX", "OOXOX", "POXXP"], ["POOPX", "OXPXP", "PXXXO", "OXXXO", "OOOPP"],
["PXOPX", "OXOXP", "OXPOX", "OXXOP", "PXPOX"], ["OOOXX", "XOOOX", "OOOXX", "OXOOX", "OOOOO"],
["PXPXP", "XPXPX", "PXPXP", "XPXPX", "PXPXP"]]
result
[1, 0, 1, 1, 1]
입출력 예 설명
입출력 예 #1
첫 번째 대기실
No. 0 1 2 3 4
0 P O O O P
1 O X X O X
2 O P X P X
3 O O X O X
4 P O X X P
모든 응시자가 거리두기를 지키고 있습니다.
두 번째 대기실
No. 0 1 2 3 4
0 P O O P X
1 O X P X P
2 P X X X O
3 O X X X O
4 O O O P P
(0, 0) 자리의 응시자와 (2, 0) 자리의 응시자가 거리두기를 지키고 있지 않습니다.
(1, 2) 자리의 응시자와 (0, 3) 자리의 응시자가 거리두기를 지키고 있지 않습니다.
(4, 3) 자리의 응시자와 (4, 4) 자리의 응시자가 거리두기를 지키고 있지 않습니다.
세 번째 대기실
No. 0 1 2 3 4
0 P X O P X
1 O X O X P
2 O X P O X
3 O X X O P
4 P X P O X
모든 응시자가 거리두기를 지키고 있습니다.
네 번째 대기실
No. 0 1 2 3 4
0 O O O X X
1 X O O O X
2 O O O X X
3 O X O O X
4 O O O O O
대기실에 응시자가 없으므로 거리두기를 지키고 있습니다.
다섯 번째 대기실
No. 0 1 2 3 4
0 P X P X P
1 X P X P X
2 P X P X P
3 X P X P X
4 P X P X P
모든 응시자가 거리두기를 지키고 있습니다.
두 번째 대기실을 제외한 모든 대기실에서 거리두기가 지켜지고 있으므로, 배열 [1, 0, 1, 1, 1]을 return 합니다.
제한시간 안내
정확성 테스트 : 10초
두 테이블 T1, T2가 행렬 (r1, c1), (r2, c2)에 각각 위치하고 있다면,
T1, T2 사이의 맨해튼 거리는 |r1 - r2| + |c1 - c2| 입니다. ↩예시 이미지
해결코드
function solution(places) {
const resultList = [];
for(let room = 0; room < places.length ; room ++) {
let result = 1;
const pPosList = [];
const place = places[room];
// 응시자가 앉아있는 위치만 찾아내기
for(let m=0; m < place.length; m++){
for(let n=0; n < place[m].length; n++){
if(place[m][n] === 'P') pPosList.push([m,n]);
}
}
// 각각의 응시자들끼리의 거리를 비교 후, 거리두기 조건 체크
// 기본적으로 거리두기 실패가 한번이라도 나오면, 이후 조건들은 검사하지 않음
const pPosListLength = pPosList.length;
for(let i=0; i < pPosListLength - 1; i++){
for(let j=i + 1; j < pPosListLength; j++){
// 응시자들끼리의 맨해튼 거리 구하기
const manhattanDistance = getManhattanDistance(pPosList[i], pPosList[j]);
// 맨해튼 거리가 1이라면, 무조건 거리두기 실패
if( manhattanDistance === 1) {
result = 0;
break;
// 맨해튼 거리가 2 초과라면, 거리두기 성공
}else if( manhattanDistance > 2){
continue;
// 맨해튼 거리가 2인 경우, 파티션 조건을 검사
}else {
const [r1, c1] = pPosList[i];
const [r2, c2] = pPosList[j];
// 두 응시자의 열이 같은 경우, 사이에 파티션이 없다면 거리두기 실패
if(r1 === r2){
if(place[r1][(c1 + c2) / 2] !== 'X'){
result = 0;
break;
}
// 두 응시자의 행이 같은 경우, 사이에 파티션이 없다면 거리두기 실패
}else if(c1 === c2){
if(place[(r1 + r2) / 2][c1] !== 'X'){
result = 0;
break;
}
// 두 응시자가 대각선으로 앉은 경우, 파티션이 양쪽 사이에 하나라도 없으면 거리두기 실패
}else{
if(place[r1][c2] !== 'X' || place[r2][c1] !== 'X'){
result = 0;
break;
}
}
}
}
if(result === 0) break;
}
resultList.push(result);
}
return resultList;
}
// 두 지점 사이의 맨헤튼 거리를 구하는 함수
function getManhattanDistance([r1, c1],[r2, c2]){
return Math.abs(r1 - r2) + Math.abs(c1 - c2);
}
추가설명
모든 값들을 검사할 필요 없고, 실제로 거리두기 대상인 응시자만 따로 빼내어서, 거리두기 검사하는 것이 포인트인 것 같다.
나머지는 주석을 살펴보면 쉽게 이해할 수 있을 것 같다.
잡담
이번 알고리즘은 해결한 사람도 적어서 난이도가 있을 것 같은 문제지만, 생각보다 쉬웠다.
(매일매일 알고리즘의 힘?)
다른 사람의 풀이를 살펴봤는데
문제에서 배열이 5로 한정되어 있다고, 하드코딩으로 5로 짜여진 코드가 베스트코드라서 깜짝 놀랐다.
백해무익한 하드코딩은 언제나 피하는게 좋은 것 같다.
( 물론 실무에서는 빠른 개발 요구로 하드 코딩을 사용하는 경우가 무조건 나오는 것 같다ㅋㅋㅋㅋ )
