Fenwick Tree (BIT)
2진법 인덱스 구조를 이용해 구간합을 빠르게 구하기 위한 자료구조
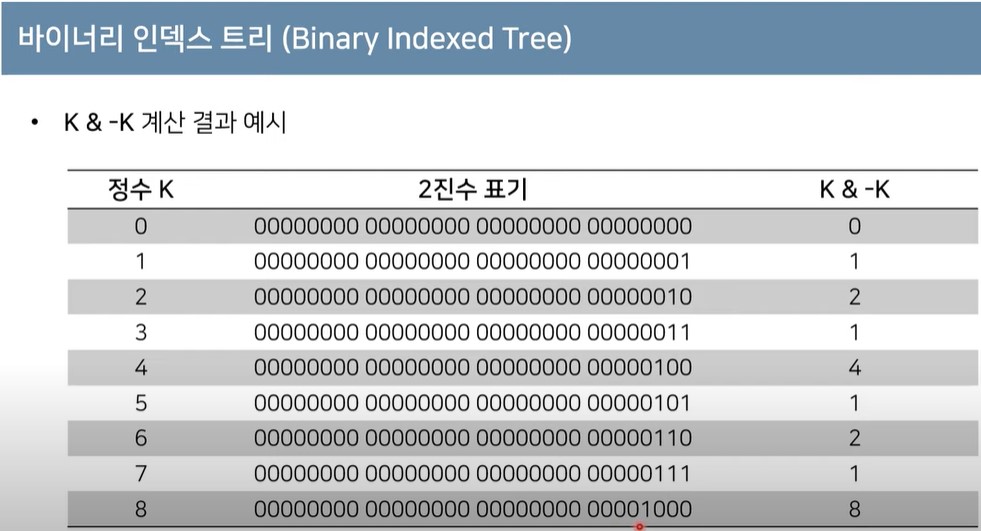
- 0이 아닌 마지막 비트를 구하는 방법
: 특정한 숫자 K의 0이 아닌 마지막 비트를 찾기 위해선 -K & K 계산
✅ 해설
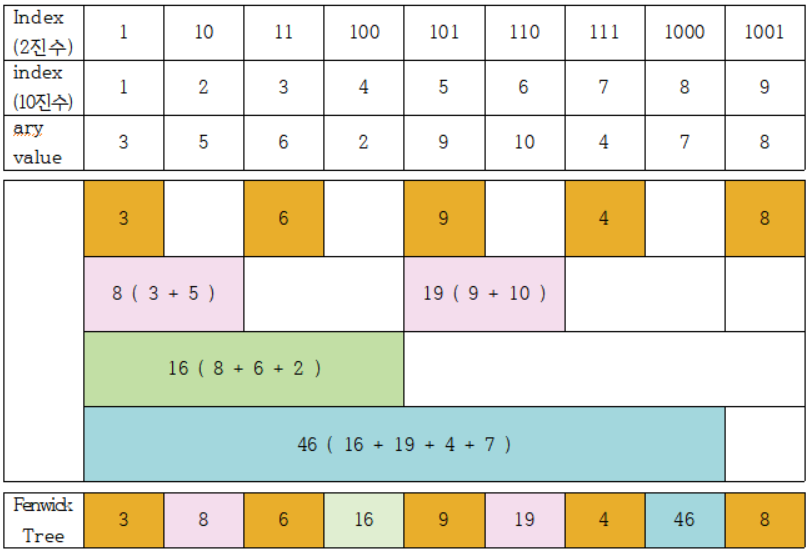
index가 1부터 시작한다는 가정 하에
1번 index : fenwick tree[1] = ary[1]이다.
6번 index : fenwick tree[6] = ary[6] + ary[5]
8번 index : fenwick tree[8] = ary[8] + ary[7] + ... + ary[1]
펜윅 트리에서 사용하는 수식
: LB[i] = i & -i (&는 비트연산, -i = ~i + 1)
-> 가장 뒤에 나오는 1이 위치한 구하는 식이다.
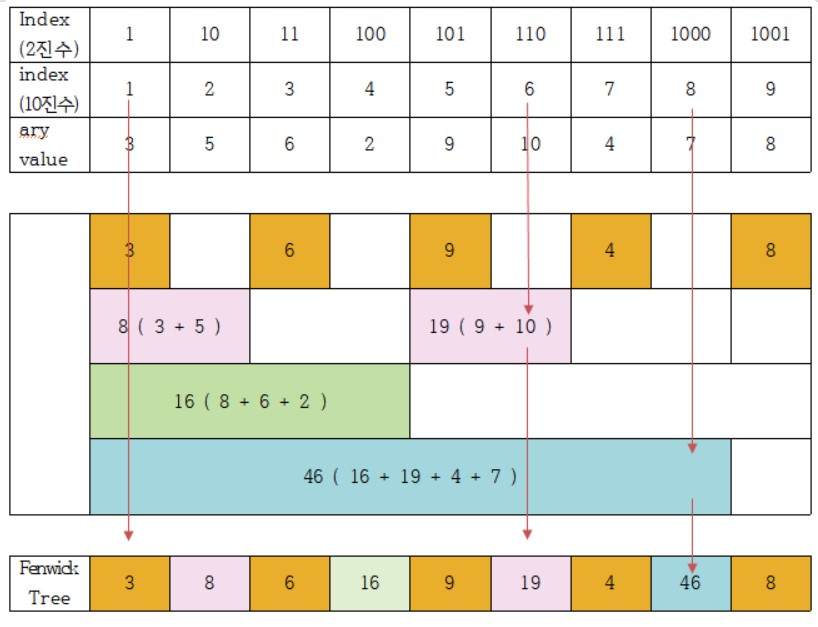
구간합 구하기
7 = 111₂, 6 = 110₂, 4 = 110₂ 이며, 가장 마지막에 위치한 1비트가 0으로 바뀌고 있다.
ary[1] ~ ary[7] = f.tree[111₂] + f.tree[110₂] + f.tree[100₂] 이 된다.
💻 코드
public static long sum(long[] tree, int i)
{
long ans = 0;
while(i>0)
{
ans += tree[i]; // 답에 해당 index tree값을 더하고
i -= (i&-i);
// i의 마지막 1이 되는 비트의 값을 뺀 값을 구하고 이를 기존 index에서 뺀다.
}
}이를 통해 ary[3] ~ ary[7]의 합 = sum(tree,7) - sum(tree,2)이다.
ary[i]부터 ary[j]까지의 합 = sum(tree, j) - sum(tree, i-1)
트리 업데이트
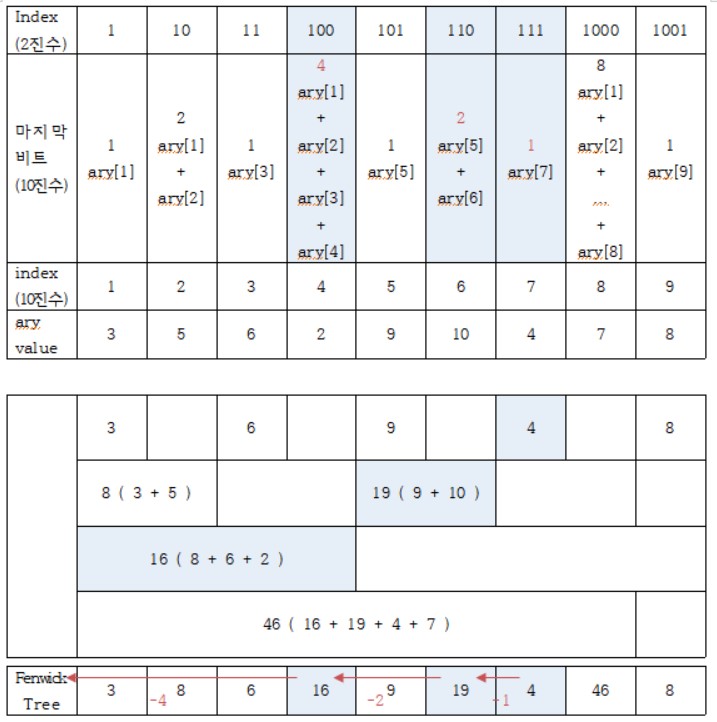
입력 받은 배열에서 특정 값이 변할 경우, 펜윅 트리에서는 이 값을 포함하는 모든 인덱스를 변경해 줘야 한다.
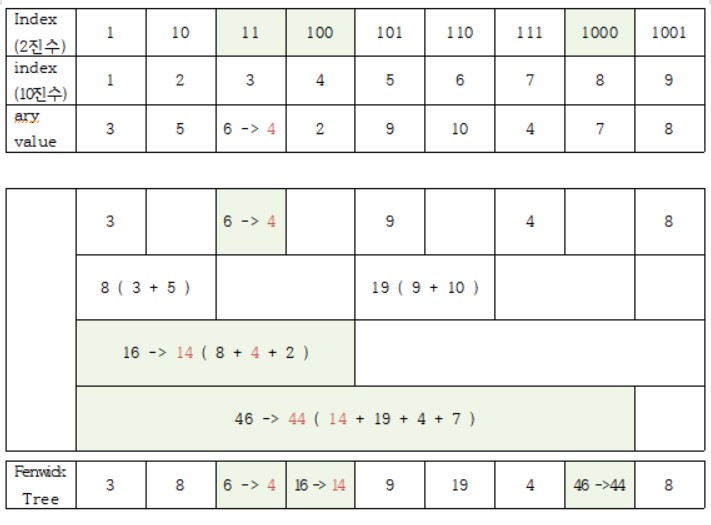
ary[3]을 6에서 4로 변경함에 따라
ary[4]도 16에서 14로 변경되고
ary[8]도 46에서 44로 변경되었다.
기존 선형트리일 경우 ary[3]을 변경할 시에 ary[4] 값과 ary[8]도 변경을 직접 해주어야 하나
fenwick Tree의 경우 실시간으로 연동되어 모두 업데이트된다.
8 = 1000₂, 4 = 100₂, 3 = 11₂값이 바뀐 인덱스이다. 이를 통해
변경된 index 값인 11₂에 마지막에 위치한 1의 값을 더함으로써
다음 변경해야할 index 값을 구하는 것을 알 수 있다.
💻 코드
// tree는 fenwick tree를, i는 index를, diff는 변경 후 값과 변경 값 전의 값의 차이
public static void update(long[] tree, int i, long diff)
{
while(i<tree.length)
{
tree[i] += diff;
i += (i&-i);
}
}펜윅트리의 초기화는 update함수를 ary[1]에서 ary[n]까지 모두 적용하는 방식으로 진행한다.
📝 정리
기존의 index를 하나씩 늘여가며 구간 합을 계산하는 코드(sum += ary[i], i++)의 시간복잡도는 O(N)이지만, 세그먼트 트리를 사용하면 O(logN)으로 감소시킬 수 있다.
이 때 펜윅트리를 사용하면 코드 길이는 물론 메모리와 시간까지 세그먼트 트리에 비해 더 나은 성능을 보인다.