연습문제
1.배열에서 특정 수의 개수 구하기

이진 탐색찾으려는 데이터와 중간점 위치에 있는 데이터를 반복적으로 비교해서 원하는 데이터를 찾는 방법N개의 원소를 포함하고 있는 수열이 오름차순으로 정렬되어 있습니다. 이때 이 수열에서 x가 등장하는 횟수를 계산하세요.단, 이 문제의 시간 복잡도 O(logN)으로 알고
2.떡볶이 떡 만들기 문제

이진 탐색 찾으려는 데이터와 중간점 위치에 있는 데이터를 반복적으로 비교해서 원하는 데이터를 찾는 방법 ✅ 문제 한 봉지 안에 들어가는 떡의 총 길이는 절단기로 잘라서 맞춰준다. 절단기에 높이(H)를 지정하면 줄지어진 떡을 한 번에 절단한다. 손님이 왔을 때 요청한
3.모험가 길드 문제

그리디현재 상황에서 지금 당장 좋은 것만 고르는 방법한 마을에 모험가가 N명 있습니다. 공포도가 X인 모험가는 반드시 X명 이상으로 구성한 모험가 그룹에 참여해야 여행을 떠날 수 있도록 규정했습니다.N명의 모험가에 대한 정보가 주어졌을 때, 여행을 떠날 수 있는 그룹
4.두 배열의 원소 교체

정렬데이터를 특정 기준에 따라서 순서대로 나열Selection Sort, Insertion Sort, Quick Sort, Count sort두 배열은 N개의 원소로 구성되어 있으며, 배열의 원소는 모두 자연수이다. 최대 K번의 바꿔칙 연산을 수행할 수 있다.N, K,
5.DFS와 BFS

깊이 우선 탐색 (DFS, Depth-First Search): 최대한 깊이 내려간 뒤, 더이상 깊이 갈 곳이 없을 경우 옆으로 이동참고 gif 파일스택 또는 재귀함수로 구현너비 우선 탐색
6.DP - 개미 전사
DP(Dynamic Programming) 기법해결한 부분 문제의 정답을 메모리에 기록하여, 한 번 계산한 답은 다시 계산하지 않도록 하는 캐싱 기법을 활용하여 문제의 시간 복잡도를 줄이는 문제 해결 기법. -> 탑다운(재귀함수),바텀업(반복문) 활용 가능DP -> 점
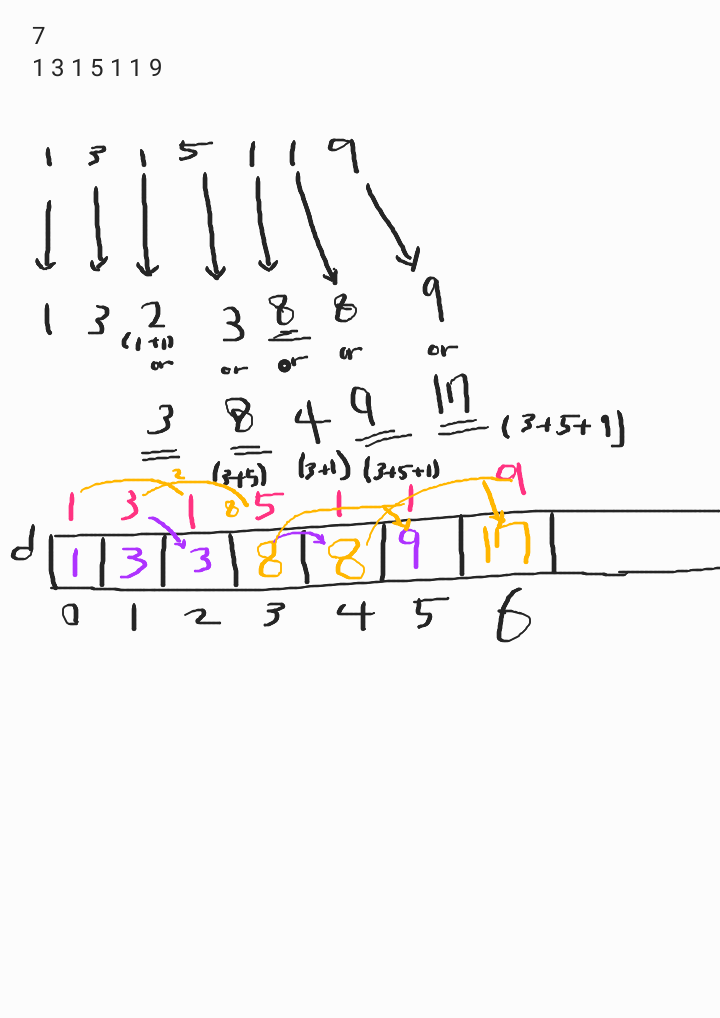
7.DP - 1로 만들기

DP(Dynamic Programming) 기법해결한 부분 문제의 정답을 메모리에 기록하여, 한 번 계산한 답은 다시 계산하지 않도록 하는 캐싱 기법을 활용하여 문제의 시간 복잡도를 줄이는 문제 해결 기법.
8.DP- 효율적인 화폐 구성

DP(Dynamic Programming) 기법해결한 부분 문제의 정답을 메모리에 기록하여, 한 번 계산한 답은 다시 계산하지 않도록 하는 캐싱 기법을 활용하여 문제의 시간 복잡도를 줄이는 문제 해결 기법. -> 탑다운(재귀함수),바텀업(반복문) 활용 가능N가지 종류의
9.Graph - Cycle 여부 확인하기

Graph 기타 알고리즘graph - 서로소 집합 확인하기 -> 재귀함수를 이용해서 루트 노드 확인하기이를 활용하여 Cycle 유무를 확인할 수 있다.서로소 집합은 무방향 그래프 내에서의 사이클 유무를 판별하는데 사용 가능각 간선을 하나씩 확인하며 두 노드의 루트 노드
10.Graph - 최소신장트리 구하기 (크루스칼 알고리즘)

신장트리 : 그래프에서 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프최소신장트리를 구하기 위해서? -> 크루스칼 알고리즘 활용크루스칼 알고리즘 (그리디 알고리즘에 포함)간선 데이터를 비용에 따라 오름차순 정렬간선을 하나씩 확인하며 현재의 간선이 사이클을 포
11.Graph - Topology Sort

위상정렬 : 사이클이 없는 모든 노드를 방향성에 거스르지 않고 순서대로 나열하는 것 (선수과목이 있는 과목을 후순위에 두어 과목 수강 등이 예시)진입차수 : 특정한 노드로 들어오는 간선의 개수진출차수 : 특정한 노드에서 나가는 간선의 개수이를 응용하여 다음과 같이 계산
12.에라토스테네스의 체

기본 약수의 성질 이용\-> 모든 약수가 가운데 약수를 기준으로 곱셈 연산에 대해 대칭을 이룬다.ex) 16의 약수 : 1 2 4 8 16 에서 2 x 8과 8 x 2는 대칭을 이룬다.즉, 우리는 특정한 자연수의 모든 약수를 찾을 때 가운데 약수(제곱근)만 확인하면 된
13.투 포인터 알고리즘 응용 - 특정한 합 가지는 부분 연속 수열 찾기

투 포인터 알고리즘 : 리스트에 순차적으로 접근할 때 두 개의 점의 위치를 기록하면서 처리하는 알고리즘 (시작점과 끝점 설정)n개의 자연수로 구성된 수열이 있다.합이 m인 부분 연속 수열의 개수를 구하여라.수행 제한 시간은 O(N)이다.ex) 1 2 3 2 5 -> (
14.DP - 구간 합 빠르게 계산하기
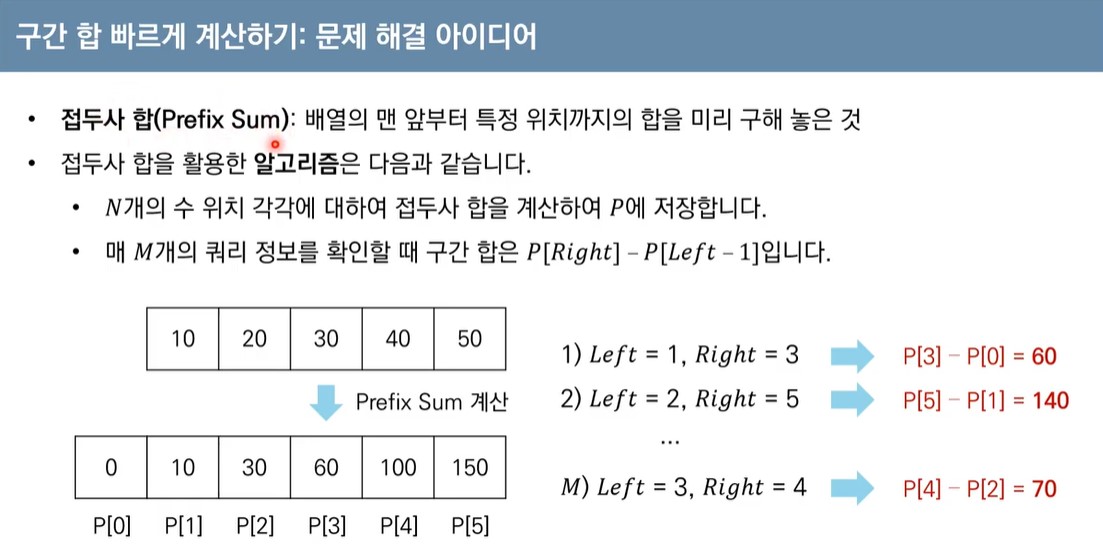
DP(Dynamic Programming) 기법해결한 부분 문제의 정답을 메모리에 기록하여, 한 번 계산한 답은 다시 계산하지 않도록 하는 캐싱 기법을 활용하여 문제의 시간 복잡도를 줄이는 문제 해결 기법.\-> PrefixSum (배열의 맨앞부터 특정 위치까지의 합
15.Fenwick Tree(Binary Indexed Tree)
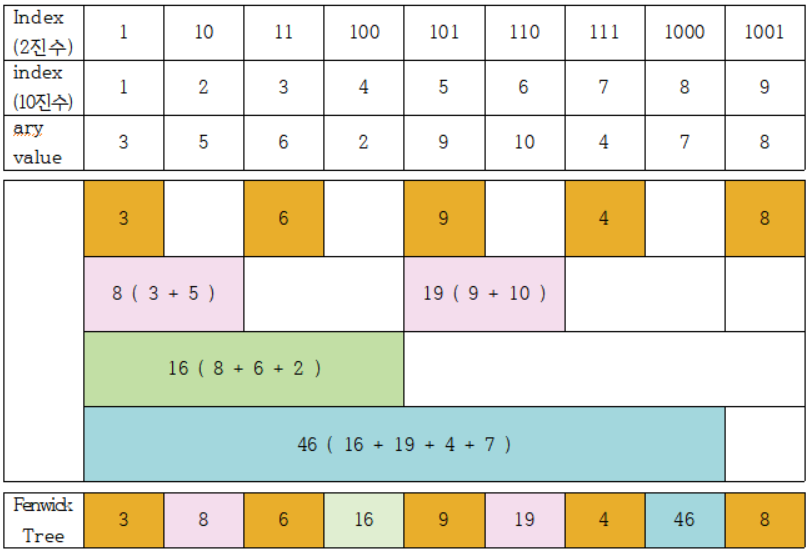
Fenwick Tree (BIT)2진법 인덱스 구조를 이용해 구간합을 빠르게 구하기 위한 자료구조0이 아닌 마지막 비트를 구하는 방법: 특정한 숫자 K의 0이 아닌 마지막 비트를 찾기 위해선 -K & K 계산index가 1부터 시작한다는 가정 하에1번 index : f