[백준 10423] 전기가 부족해 (C++)

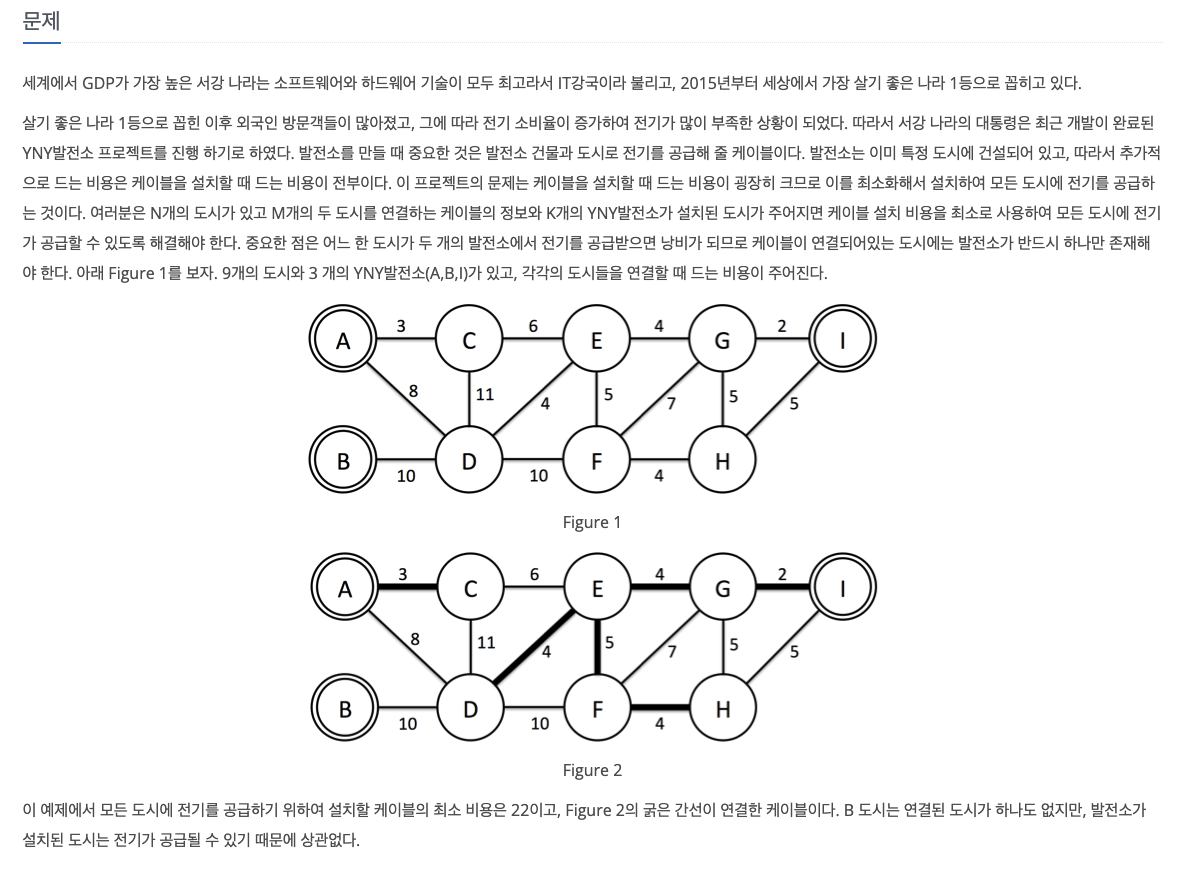
이번 문제도 도시를 연결하는데 필요한 최소 비용이므로 MST로 접근해야될 것 같다. 하지만, 온전한 트리는 아니기에 곧바로 MST로 접근하면 안된다. 이 경우, 가상의 노드 $N + 1$을 두어 발전기들은 해당 노드에 비용이 0으로 연결되게 한다면, 그림 2를 MST로 변형이 가능하다.

이후, 크루스칼 알고리즘으로 문제를 해결하면 된다. 이때, $M$은 $100,000$이하, $w$는 $10,000$이하이므로 정답은 최대 $10^9$으로 int표현범위 이내이다.

#include <bits/stdc++.h>
using namespace std;

int n, m, k, ans, cnt;
vector<tuple<int, int, int>> edge;
vector<int> p(1002, -1);

int find(int x) {
	if (p[x] < 0) return x;
	return p[x] = find(p[x]);
}

void merge(int x, int y) {
	x = find(x);
	y = find(y);
	if (x == y) return;
	p[y] = x;
}

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);

	cin >> n >> m >> k;
	for (int i = 0, power; i < k; i++) {
		cin >> power;
		edge.push_back({0, power, n + 1});
	}
	for (int i = 0, u, v, w; i < m; i++) {
		cin >> u >> v >> w;
		edge.push_back({w, u, v});
	}
	sort(edge.begin(), edge.end());

	for (int i = 0, u, v, w; i < edge.size(); i++) {
		tie(w, u, v) = edge[i];
		if (find(u) == find(v)) continue;
		merge(u, v);
		ans += w;
		cnt++;
		if (cnt == n) break;
	}
	cout << ans;
}