알고리즘

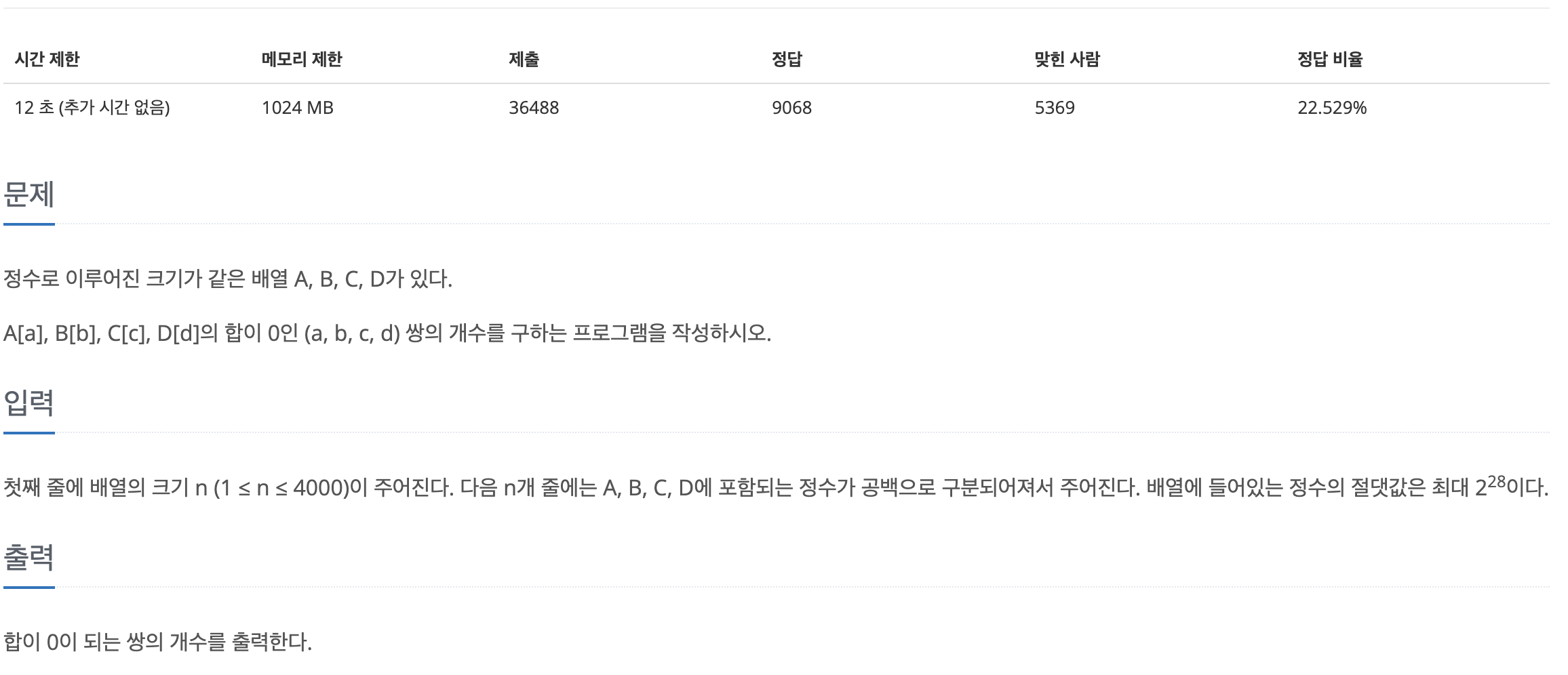
이 문제는 brute-force로 풀면 O(N^4)로 시간 초과가 난다.배열 A, B, C, D에서 1개씩 선택해 푸는 것으로는 시간 내에 풀 수 없다는 소리이다.그럼 여러 수를 더해두고 0을 만들기 위해 필요한 값이 있는지 확인하는 방식으로 접근해서 시간 복잡도를 떨

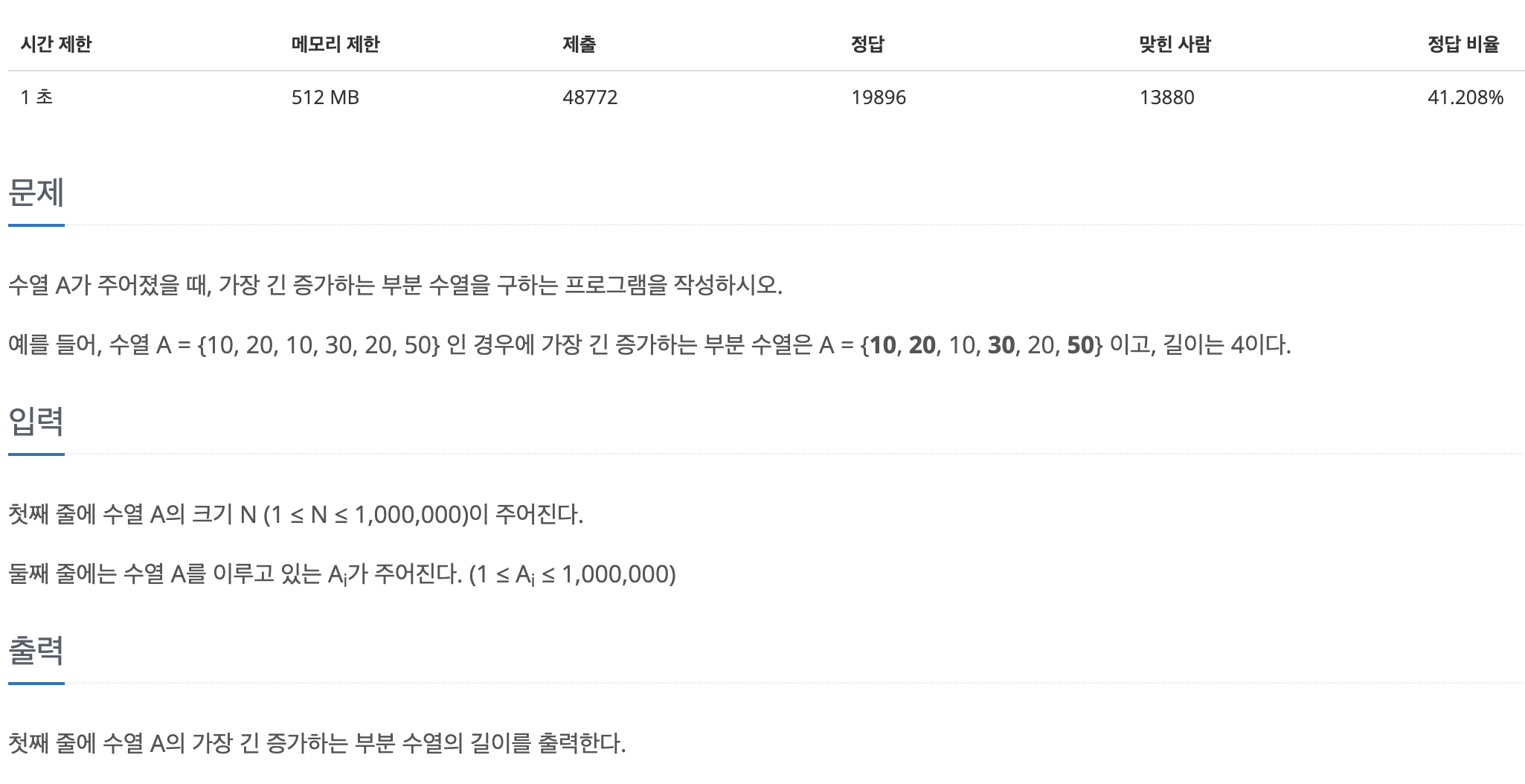
이 문제는 단순히 생각해보면, 스택을 이용해 풀 수 있을 것 같다.monotone-stack을 이용하면 손쉽게 증가하는 부분 수열을 구해낼 수 있기 때문이다.하지만, 이렇게 구한 수열이 항상 가장 긴 증가하는 부분수열(LIS)를 보장하지는 못한다.당장 문제에서 주어진

이 문제에서 각 한 다각형의 꼭짓점 좌표들이 입력으로 주어진다. 이때의 다각형의 넓이는 어떻게 구할 수 있을까?먼저, 다각형은 삼각형들의 합으로 구할 수 있고, 삼각형의 넓이는 $$\\frac{1}{2} \\cdot | \\hat{a} \\times \\hat{b} |

이 문제는 가능한 모든 경우의 수를 탐색해보는 방법 밖에 없다. 그런데, 문제 조건에 맞추어 스도쿠를 풀어야하므로 백트래킹이 적절해보인다.입력으로 들어온 퍼즐의 0인 칸에 적절한 값을 채워넣어야 한다. 그래서 재귀함수 내부에서 0인 점을 $$O(N^2)$$으로 찾은 후

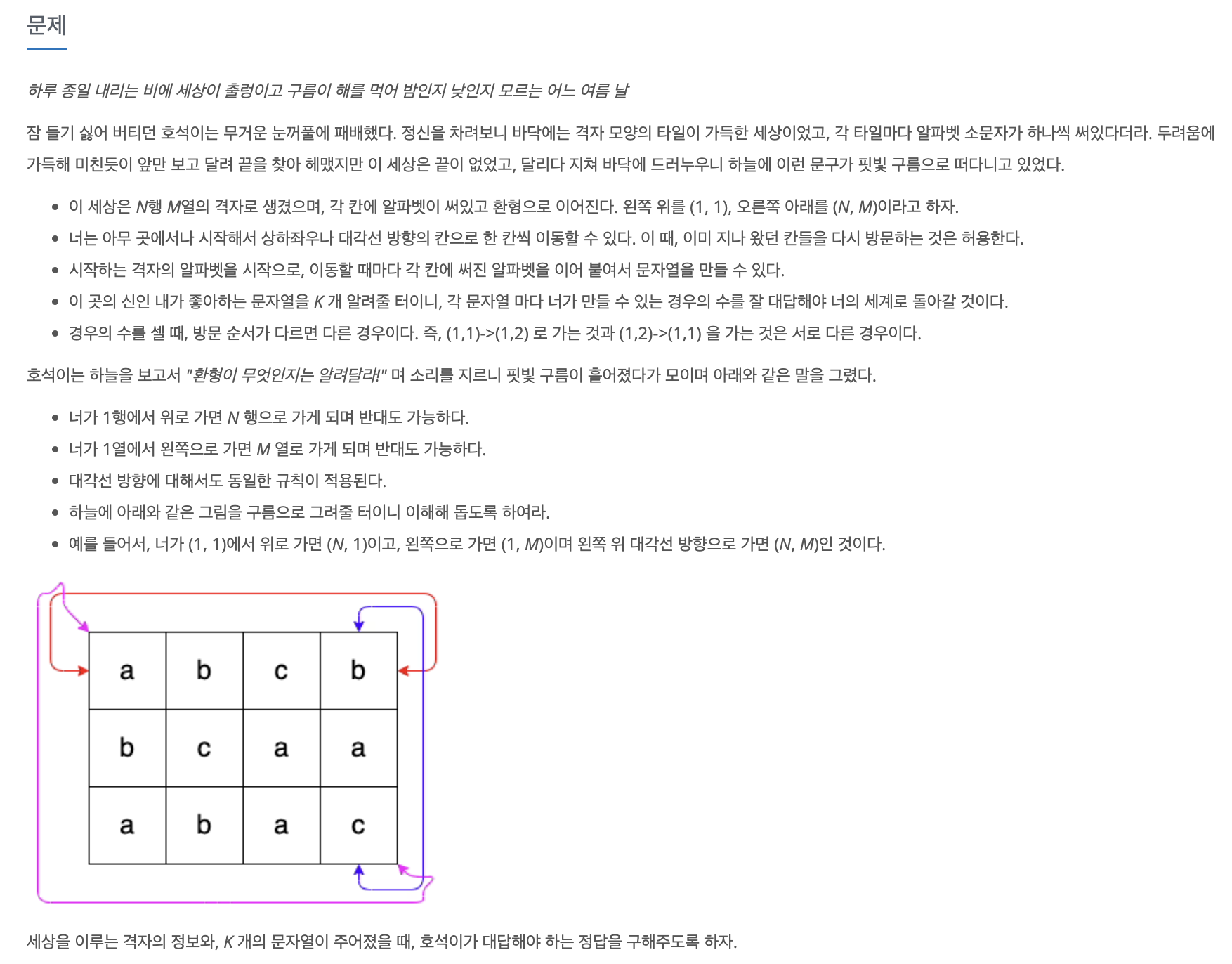
이 문제는 격자에서 상하좌우 및 대각선으로 이동해가며, 신이 좋아하는 문자열의 갯수를 얼마나 만들 수 있는지 확인하는 문제이다.따라서, bfs로 여러 칸들을 중복을 허용하여 방문해가며 문자열을 만들어야 한다.그리고, 미리 만들 수 있는 모든 경우의 문자열에 대한 경우의

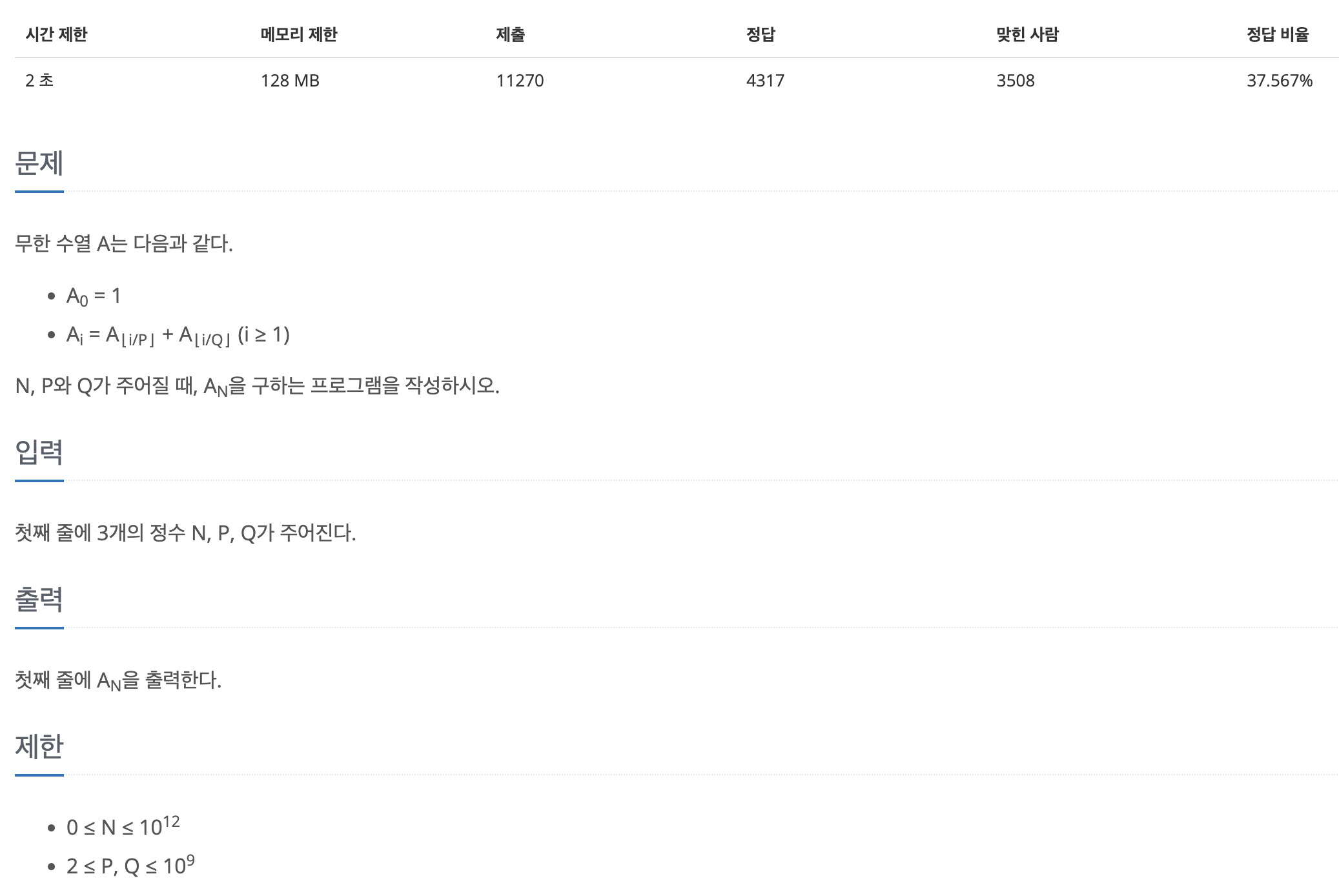
이 문제는 점화식이 주어진 dp문제이다.얼핏보면 실버처럼 쉬워보이지만, 제한조건때문에 난이도가 올라가는 문제이다.$${N} \\le {10^{12}}$$이므로 bottom-up방식의 dp로는 시간 초과가 난다.top-down을 하자니 중복 연산이 생기므로 최적화를 위해

이 문제는 기존의 발들의 위치를 기반으로 발을 다음 위치로 이동시킬때, 힘이 최소가 되도록 해야한다.즉, 이전 값을 통해 새로운 값을 추론하는 과정이므로 DP로 접근이 가능하다.그런데, 위치 정보는 왼발과 오른발의 위치로 2차원으로 나타내어져야한다.그렇기 때문에 3차원

먼저, 모든 경우의 수를 따져보면, $$N \\le 100$$이므로 최대 $$2^{100}$$가지의 경우가 있다는 것을 알 수 있다.따라서, brute-force나 백트래킹으로는 절대 풀 수 없는 문제임이 확실하다.그렇다면, 메모리 M를 확보하는데 필요한 최소 비용을

먼저, brute-force나 백트래킹이 가능한지 확인해보자. $$N$$은 최대 $$500$$이므로, $$\\sum\_{k = 0}^{498} \\begin{pmatrix} 500 - k \\ 2 \\end{pmatrix} = 20833250$$가 된다. 대략 2천만

이 문제는 우선순위 큐를 2개를 놓고 한 쪽은 최대힙, 다른 쪽은 최소힙을 구성하도록 하고 적절히 입력과 삭제를 반복하면 풀리는 문제이다.하지만, C++에서는 더 쉽게 푸는 방법이 있어 포스팅해본다.C++ STL의 set은 이진 탐색 트리 중 하나인 red-black트

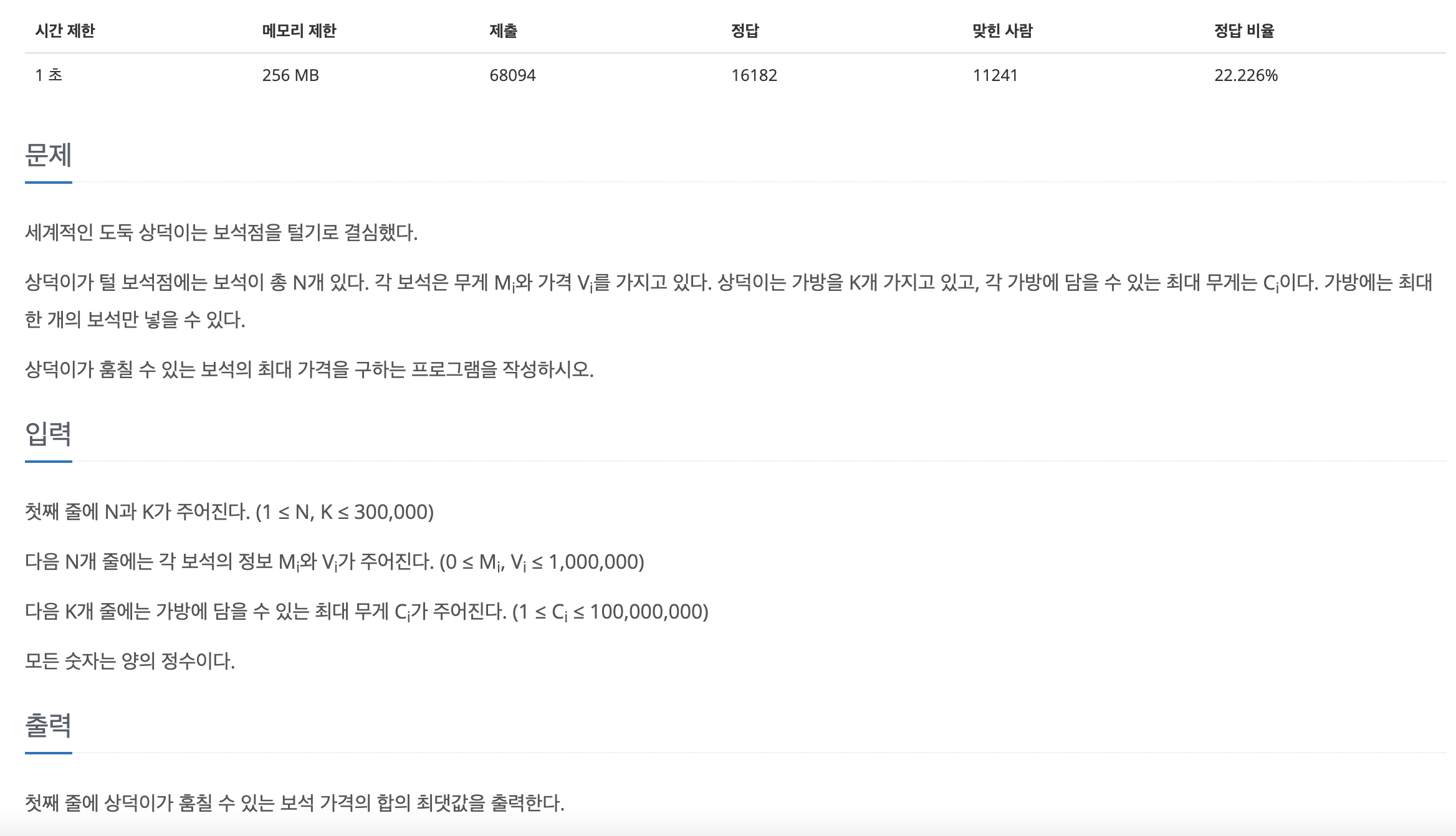
이 문제는 상덕이가 훔칠 수 있는 보석 가격의 합의 최댓값을 구하는 문제이다.최댓값을 구하려면, 보석의 가치가 가장 높은 것들만 골라 훔치면 된다.하지만, 가방마다 담을 수 있는 무게의 최댓값이 결정되어 있어서 가치가 높더라도 담지 못하는 겅우가 발생할 수 있다.즉,

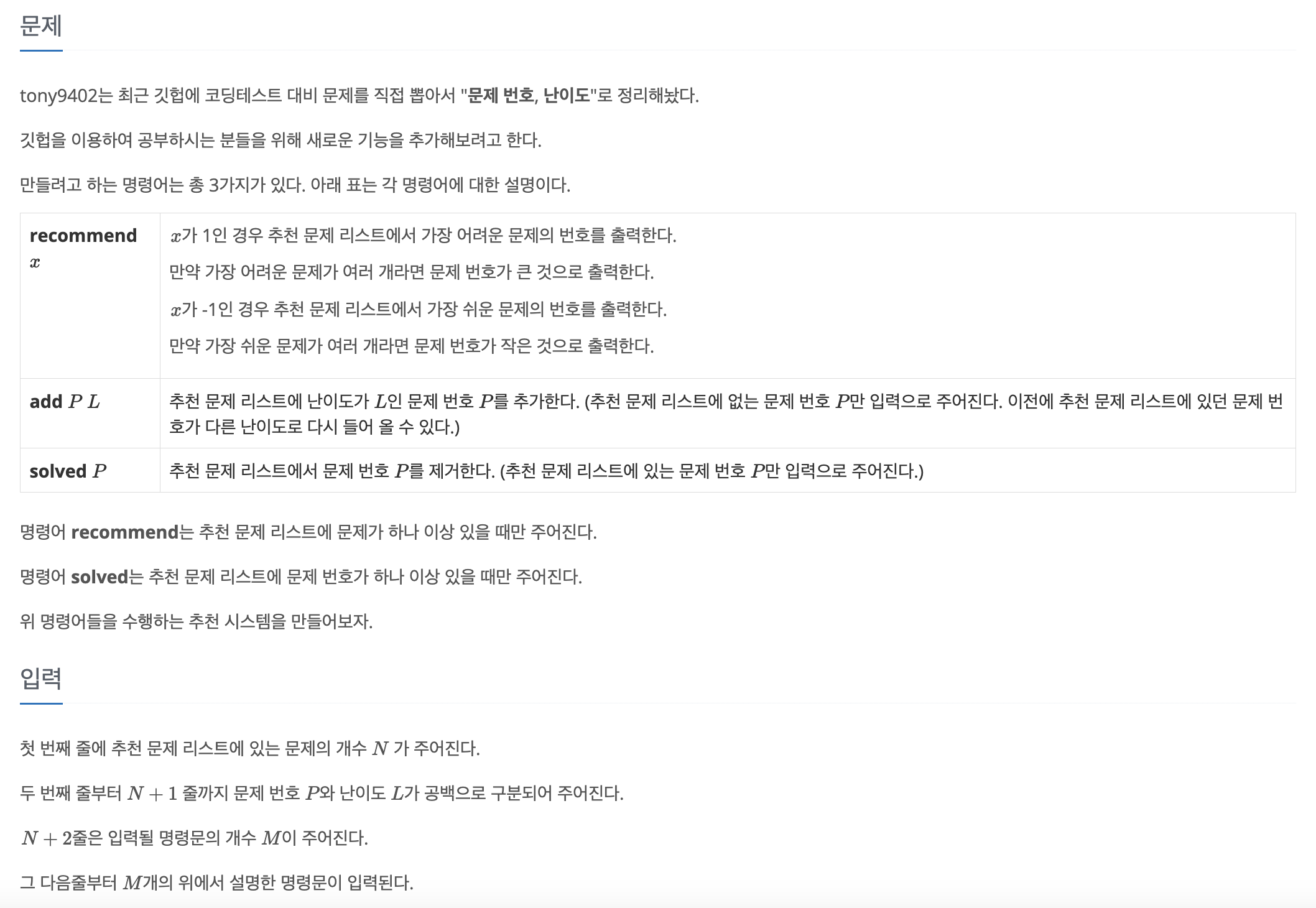
이 문제에서는 문제 리스트에서 문제의 추가/삭제가 빈번히 일어나고 빠르게 문제를 찾아줘야하기 때문에, 트리 형태의 자료구조를 사용하는 것이 좋다.그렇다면, 난이도와 문제 번호를 어떻게 관리해야 효율적일까?우리는 {난이도, 문제번호}를 set<pair<int,

업로드중..이 문제는 문제 리스트를 배열이나 벡터로 관리하면 안된다.단순히 명소를 지정하고 해제하는 정도는 배열로 충분히 처리가 가능하지만, 3번 연산을 수행하려면 가장 가까운 오른쪽 명소를 찾기 위해서 $$O(N)$$의 시간 복잡도가 필요하다.따라서, 전체 시간 복잡

이 문제는 이전에 풀었던 문제 추천 시스템 Version 1의 시리즈 문제이다.이 문제도 삽입과 삭제, 접근이 빈번히 이루어지고 원소들이 내부적으로 정렬된 상태를 유지하면 편할 것 같다.따라서, 트리 형태의 자료구조에 데이터를 저장하는 게 좋아보인다.recommend는

이 문제는 카드 묶음이 $$N$$개 주어질 때, 카드를 합치는 경우 최소의 비교 횟수를 구하는 문제이다.카드의 수가 $$A$$와 $$B$$인 두 묶음을 합치려면, 비교 횟수는 $$A + B$$가 된다.하지만, 카드 묶음이 여러 개이므로 카드 묶음이 1개가 될 때 까지,

이 문제는 정수가 입력될 때마다 이미 입력된 값들 중 중앙값을 구하는 문제이다. 단순히, 벡터나 연결 리스트로 문제를 접근하면, 입력된 정수를 저장하고 정렬된 상태를 유지해야한다. 정렬 자체는 시간 복잡도가 $$O(NlogN)$$이므로, 정렬보다는 lower_bo

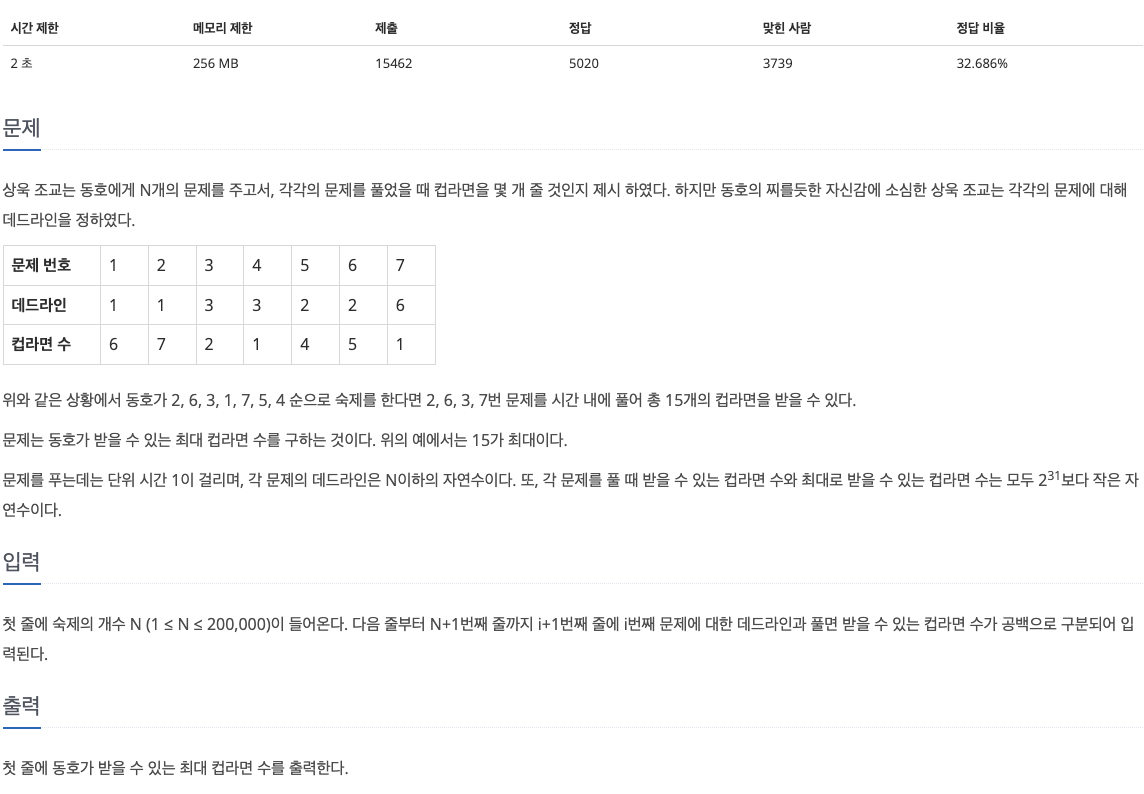
이 문제는 $N$개의 문제의 데드라인과 컵라면 수가 주어졌을 때, 동호가 받을 수 있는 최대 컵라면 수를 구하는 문제이다.이는 데드라인 이내의 문제 중 컵라면을 가장 많이 주는 문제들을 골라 푸는 것으로 구할 수 있다.추가로 문제를 푸는데 단위 시간 1이 걸린다고 했으

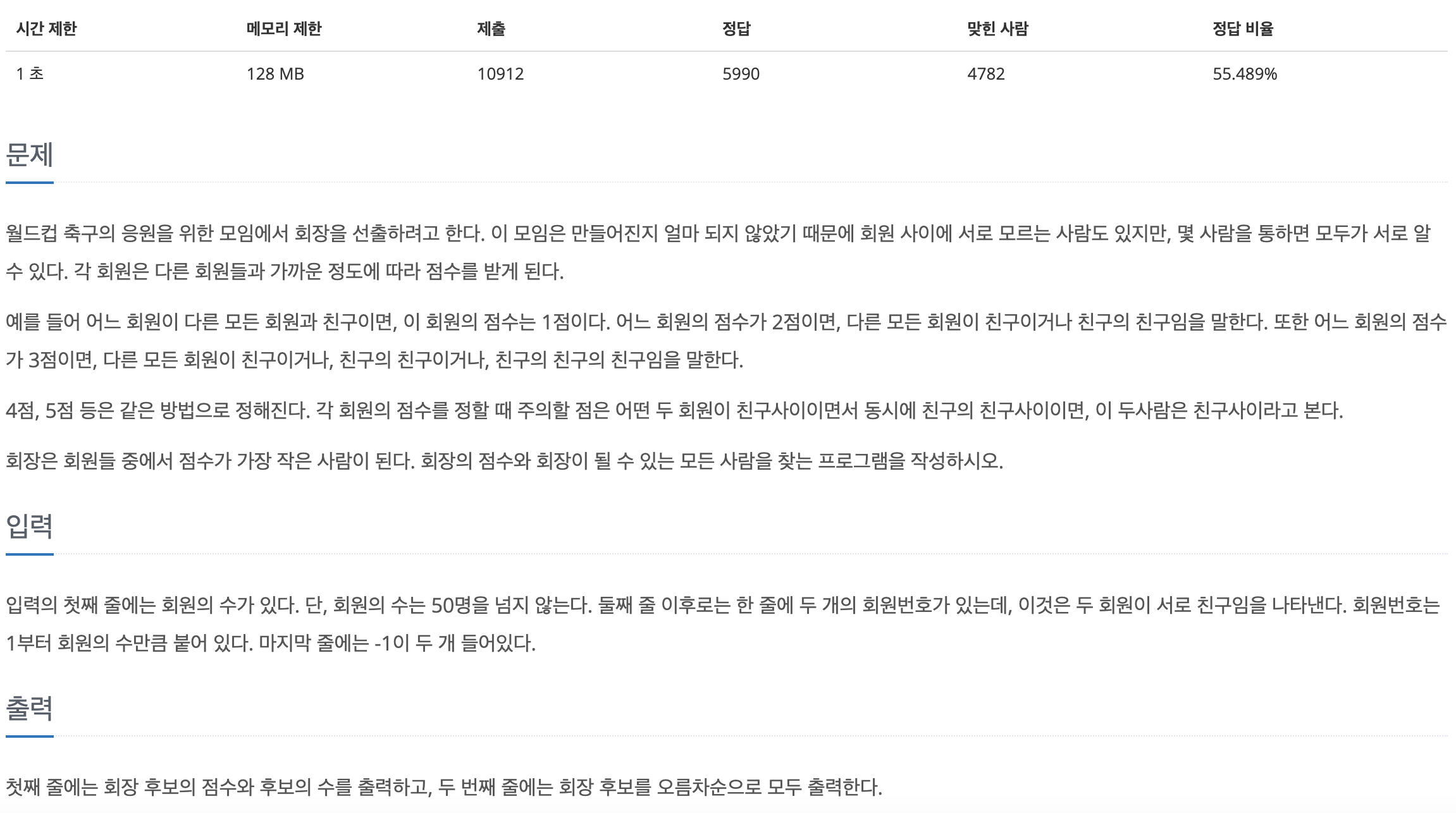
문제를 보면 알겠지만, 그래프 문제이다.회원의 점수는 자신을 제외한 회원들까지의 최단거리를 계산했을 때, 최댓값이 된다.따라서, 모든 회원이 친구면 점수가 1이고, 모든 회원이 친구 혹은 친구의 친구면 최단거리의 최댓값이 2이므로 점수는 2가 된다.따라서, 그래프를 표

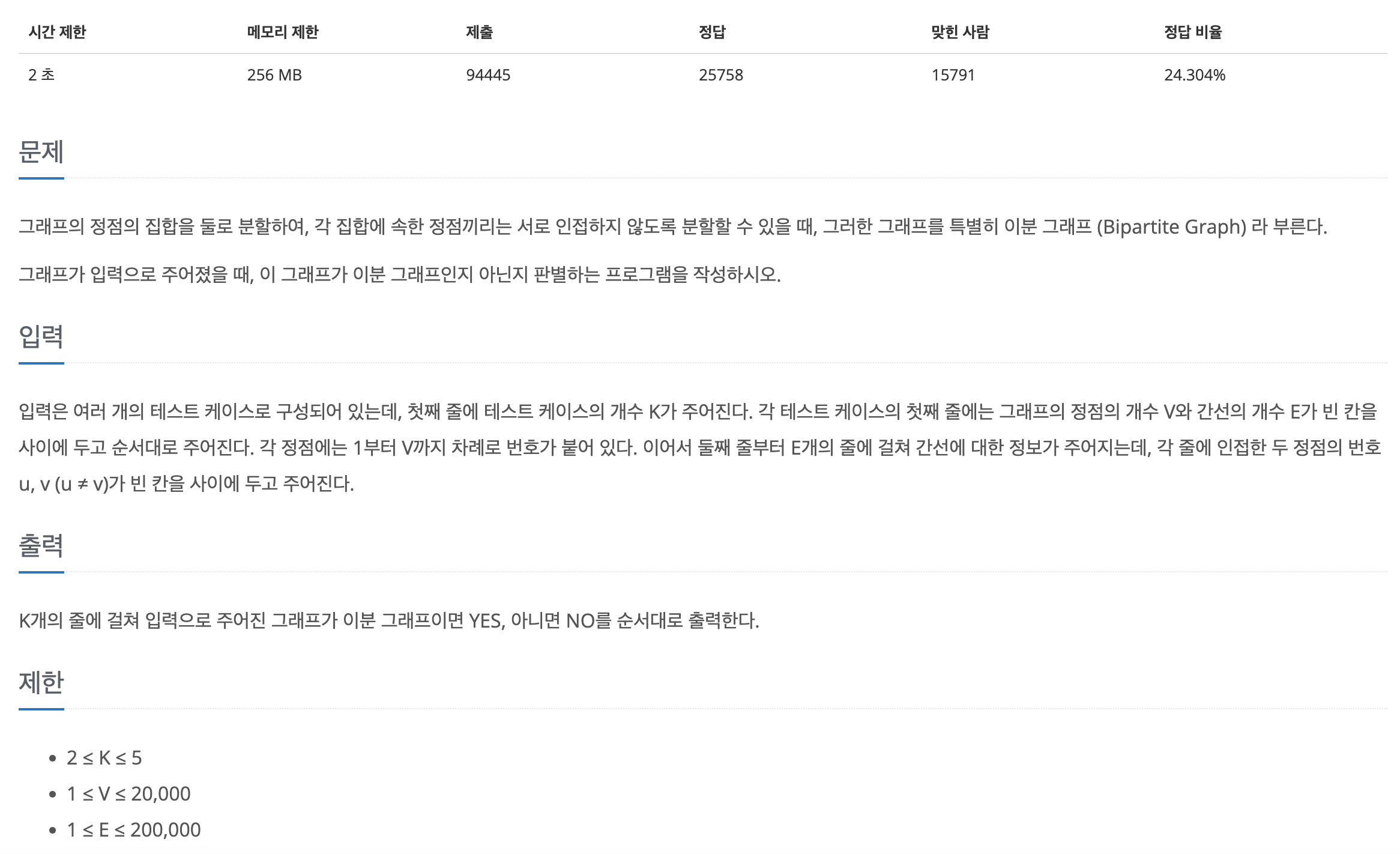
주어진 그래프가 이분 그래프인지 판별하는 문제이다.이분 그래프란, 인접한 정접을 서로 다른 색으로 칠해서 2가지의 색으로만 칠할 수 있는 그래프를 이분 그래프라 한다.즉, 인접한 정점에 색을 칠해야하므로 BFS로 접근해야 하고, 색을 편의상 $0$과 $1$로 표현하자.

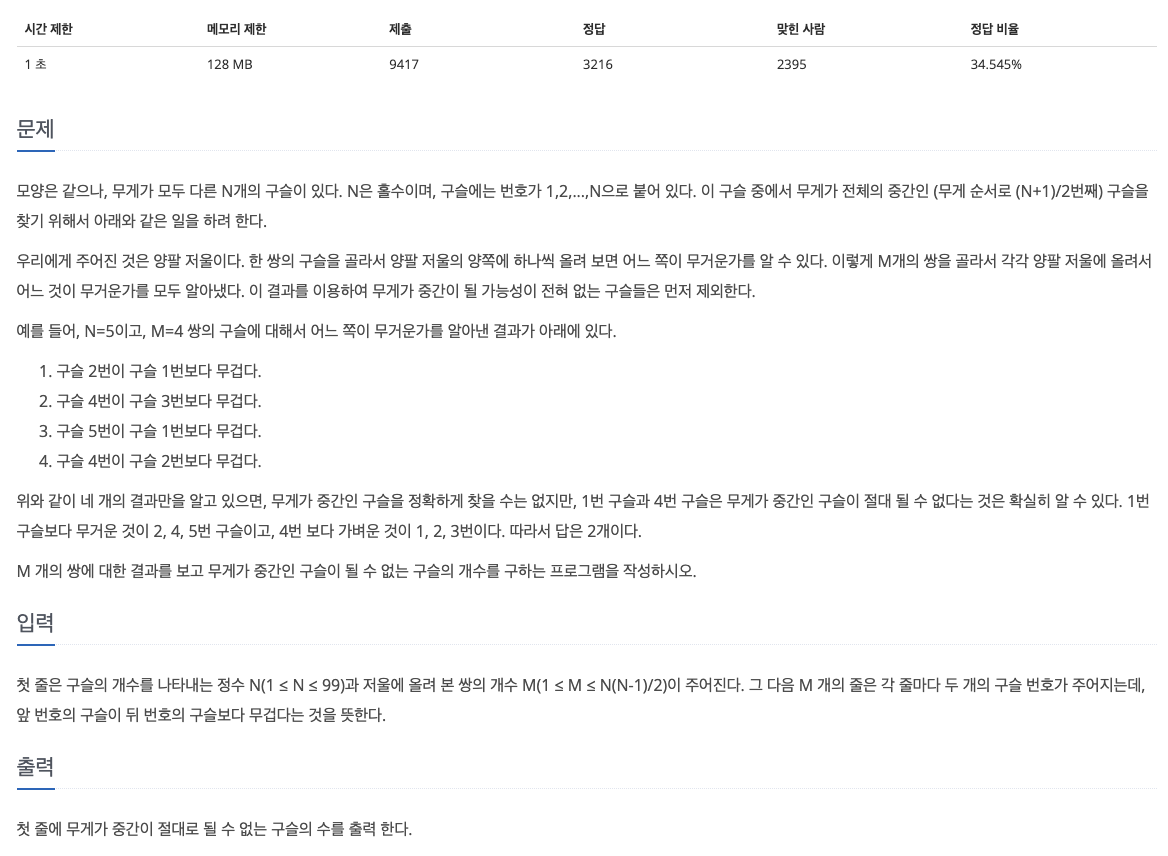
이 문제는 입력으로 구슬의 무게 관계가 주어진다. 이렇듯 관계를 표현하는 데 효과적인 자료구조는 그래프이므로, 그래프로 접근하는 것이 좋다.그래프의 표현은 인접 행렬과 인접 리스트로 표현이 가능한데, 시간 복잡도와 공간 복잡도가 $O(V + E)$로 뛰어난 인접 리스트

이 문제를 처음 봤을 때는 그냥 각 파티에 진실을 아는 사람이 존재하는지만 체크하는 문제인 줄 알았다. 하지만, 문제를 잘 읽어보면 진실을 아는 사람들이 있는 파티에서는 진실을 이야기 한다고 한다. 이는 해당 파티에 참석했던 사람들이 진실을 알게 된다는 의미이다. 따라

각 테스트 케이스마다 트리의 갯수를 세서 형식에 맞게 출력하는 문제이다.문제를 처음 접했을 때, 트리가 여러 개인 경우 "A forest of T trees."로 출력하라길래, '포레스트는 루트를 제거했을 때 서브트리들의 모임 아닌가?'라는 생각이 들었다.하지만, 연결

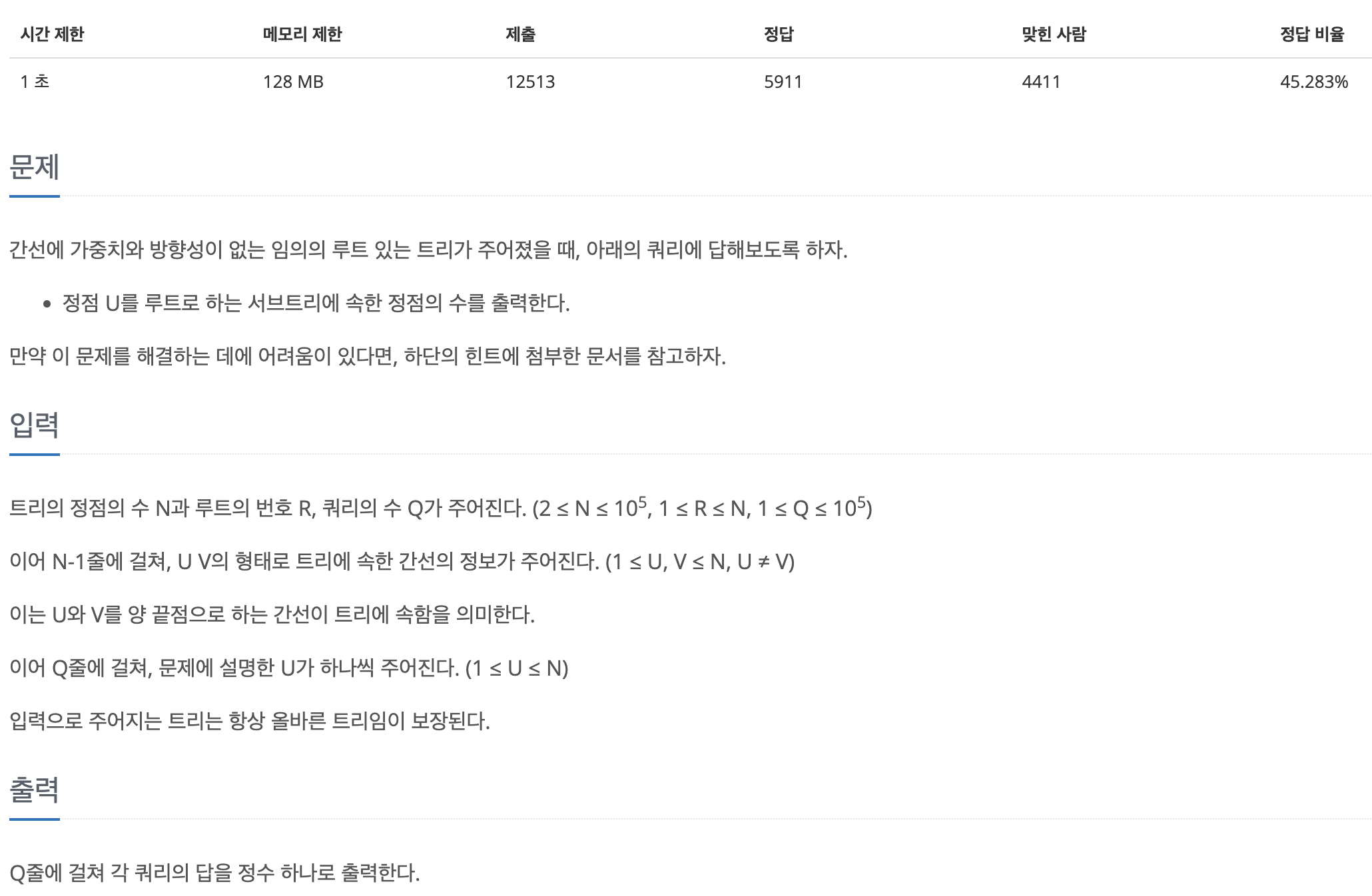
이 문제는 정점들의 연결관계를 통해 트리 정보가 주어진 후, 정점이 쿼리로 들어오는데, 해당 정점을 루트로 하는 서브 트리의 정점 갯수를 출력하는 문제이다.정점들의 연결관계로 트리가 표현되기 때문에, 인접 행렬이나 인접 리스트를 사용해 트리를 표현해야 한다. 하지만,

이 문제는 그래프가 주어졌을 때, 그래프를 트리로 만들기 위한 최소 연산 횟수를 구하는 문제이다.그래프가 연결 그래프가 아닐 수 있기 때문에, 분리 집합은 연결이 필요하고, 사이클이 발생하지 않도록 간선을 끊어주어야 한다.분리 집합의 갯수는 그래프 탐색 기법을 통해 쉽

이 문제에서 사원들이 상사와 부하 관계를 맺고 있으므로 계층적 자료구조로 표현이 가능해보인다. 따라서, 트리로 사원들의 관계를 표현할 수 있을 것이다.❗️ 하지만, 트리의 차수가 지정되지 않았기 때문에, 자식들은 벡터나 리스트에 저장해놓아야 한다.문제 상황에서는 내리

이 문제는 트리를 표현하고, 각 노드의 번호를 계산해야, 너비가 가장 넓은 레벨과 그 너비를 구할 수 있다.트리는 그래프의 일종이므로 인접 행렬이나 인접 리스트로 표현해야한다. 문제에서, 노드간의 연결 관계 보다는, 트리를 탐색해가며 답을 구하는 것에 초점이 맞춰져 있

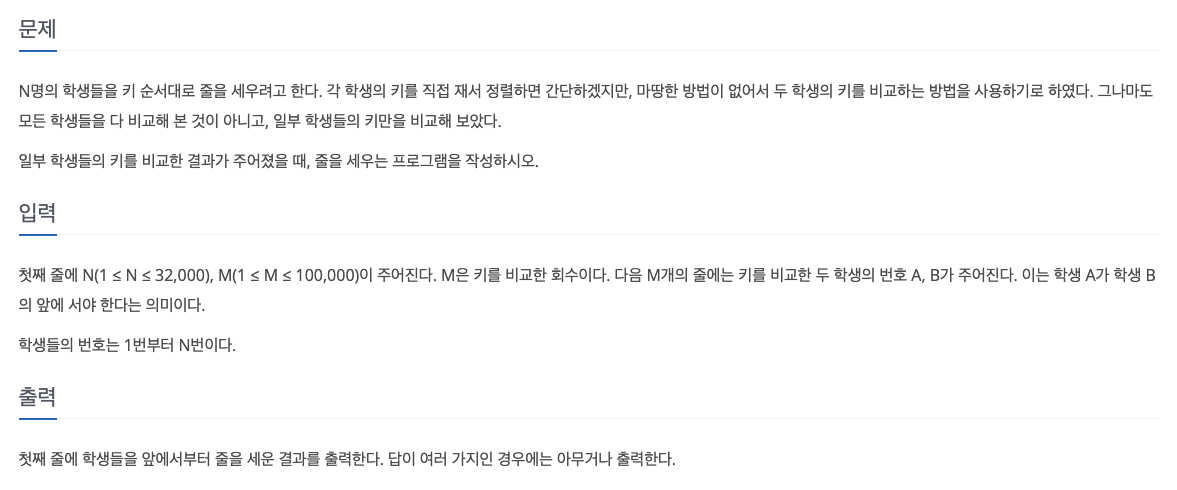
이 문제는 학생들의 키의 대소관계가 주어진다. 따라서, 그래프로 표현이 가능하다. 이때, 키 순서대로 줄을 세운다고 했는데, 그래프에서의 정렬이므로 위상 정렬문제임을 알 수 있다.위상 정렬은 사이클이 없는 방향 그래프에서 가능하고, 알고리즘은 생각보다 간단하다.각 정점

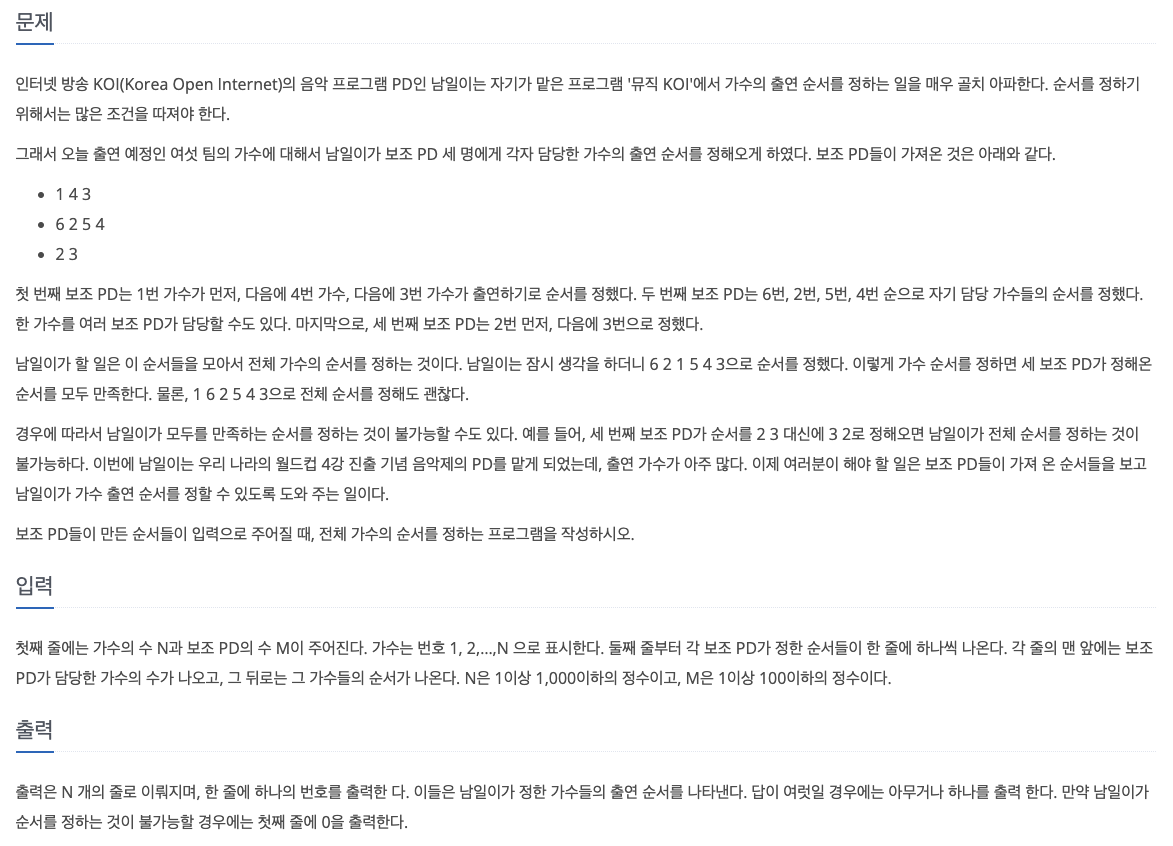
이 문제는 가수들 간의 관계가 출연 순서로 나타내어지고 있다. 따라서, 방향 그래프로 표현이 가능하다.이때, 보조 PD가 가수들의 순서를 정해두면, 이 순서를 지키면서 전체 순서를 정하는 것이다.이는 그래프 정점들의 순서를 결정하는 것과 동일한 상황이므로 위상 정렬으로

이 문제는 주민들이 자신의 조상을 완벽히 기억하고 있을 때, 계보를 복원하는 문제이다.이때, 입력은 주민들의 이름과 주민 $X$의 조상 $Y$가 이름의 형태로 주어지므로 그래프 관계로 표현해야한다. 그리고 이를 바탕으로 트리를 만들어야한다. 즉, 주민들의 관계를 정렬해

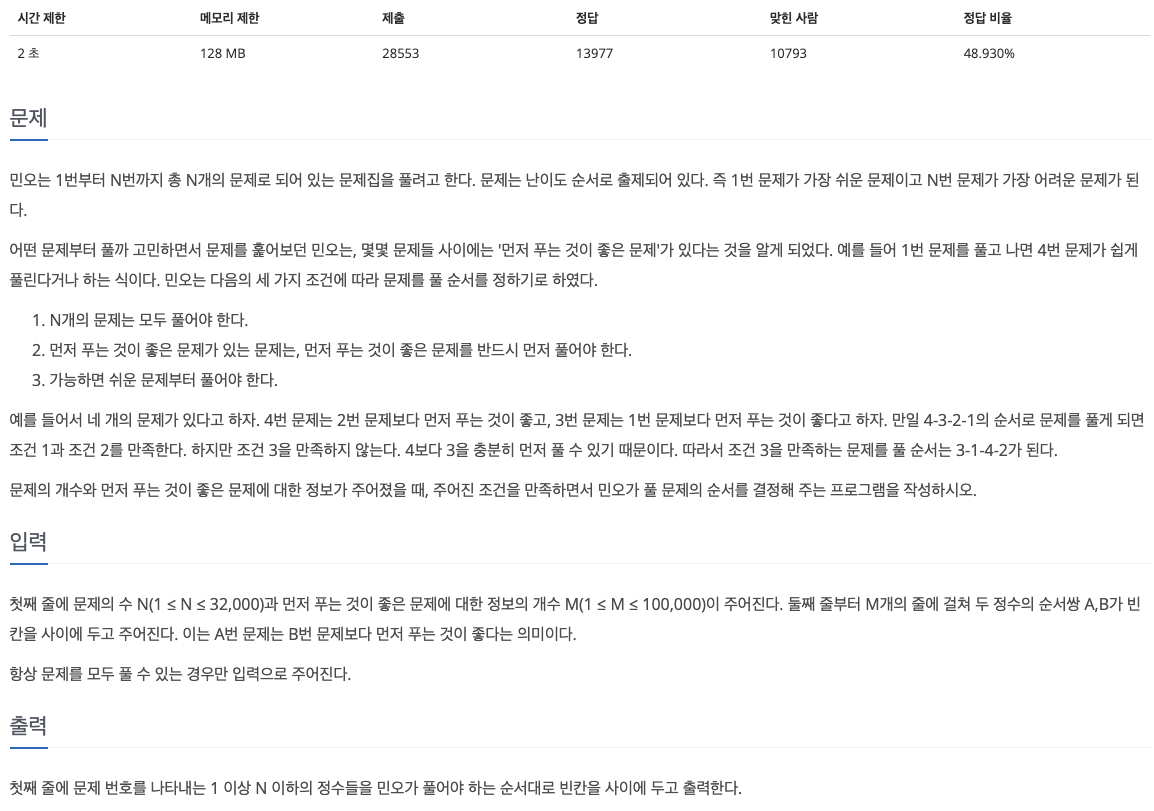
이 문제는 문제집이 주어질 때, 문제를 푸는 순서를 결정하는 문제이다. 먼저 푸는 게 좋은 문제를 먼저 풀고 가능한 한 쉬운 문제부터 풀어야 한다.문제들의 관계가 주어지는데, 이는 그래프로 표현이 가능하다.문제 $U$가 문제 $V$보다 먼저 풀기 좋다면, $U$에서 $

이 문제는 주어진대로, 최소 비용 생성 트리(MST)의 비용을 구하는 문제이다. MST란, 무방향 그래프의 부분 그래프 중 모든 정점을 포함하는 트리이다. 즉, 부분 그래프 중에서 사이클이 없는 무방향 연결 그래프가 MST란 것이다. MST를 만드는 알고리즘은

이 문제는 논에 물을 대는데 필요한 최소비용을 구하는 문제다. 그런데, 우물을 직접 파는 것과 다른 논에서 물을 끌어오는 방법이 있어, 최소 비용이 되도록 선택해야한다.이 문제를 얼핏보면, MST를 구성하되 각 간선마다 물을 끌어오는 비용과 우물을 파는 비용중 최소인

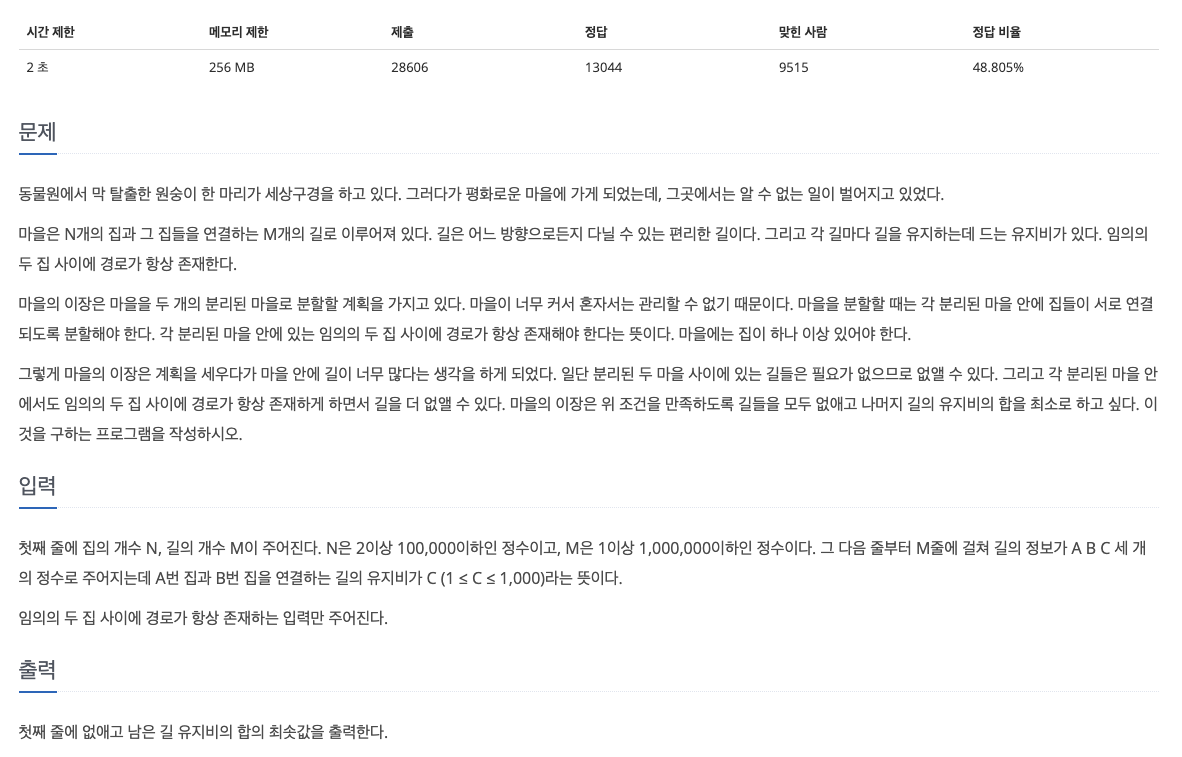
이 문제는 마을 하나를 두 개로 분할한다. 이 때, 같은 마을에 속한 집들은 서로 연결되어있어야하며, 길의 유지비를 최소로 하도록 해야한다. 즉, 분리 집합 2개에 대해 각각 MST를 구하는 문제가 된다.노드들을 어떻게 분할해서 분리 집합을 구성할지부터 의문이 들 것이

이 문제는 비용이 최소인 경로와 비용이 최대인 경로를 구해, 둘의 차를 출력하는 문제이다. 따라서, MST를 2번 구하는 것과 일맥상통한다. 크루스칼 알고리즘으로 구할 것인데, 한 번은 간선을 오름차순으로 정렬하고 다른 한 번은 내림차순으로 정렬하여 간선들을 $N$개

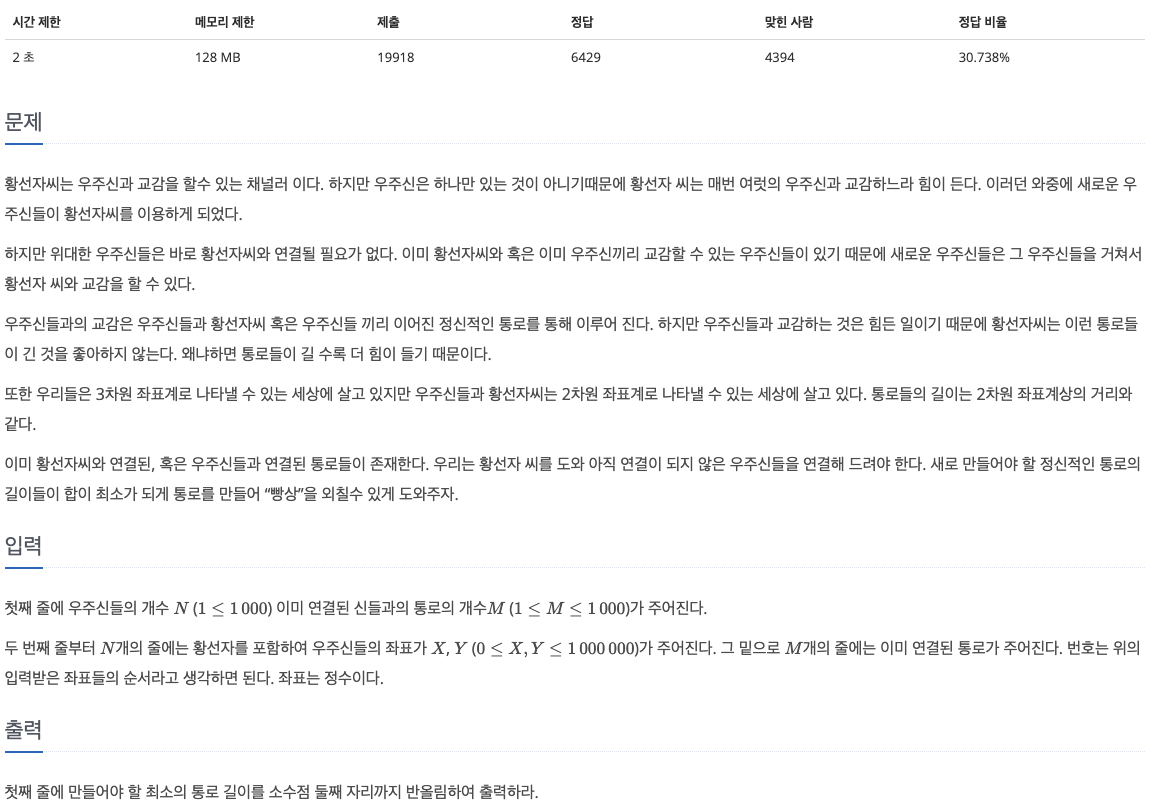
이 문제는 모든 정점을 연결할 때 필요한 최소 통로 길이를 구하는 문제이다. 즉, 최소 비용으로 모든 정점을 연결해야하는 문제이므로 MST로 접근해야한다.간단하게 Union-Find 알고리즘과 크루스칼 알고리즘으로 문제를 해결해보자.이 문제에서, $M$개의 간선이 이미

이번 문제도 도시를 연결하는데 필요한 최소 비용이므로 MST로 접근해야될 것 같다. 하지만, 온전한 트리는 아니기에 곧바로 MST로 접근하면 안된다. 이 경우, 가상의 노드 $N + 1$을 두어 발전기들은 해당 노드에 비용이 0으로 연결되게 한다면, 그림 2를 MS

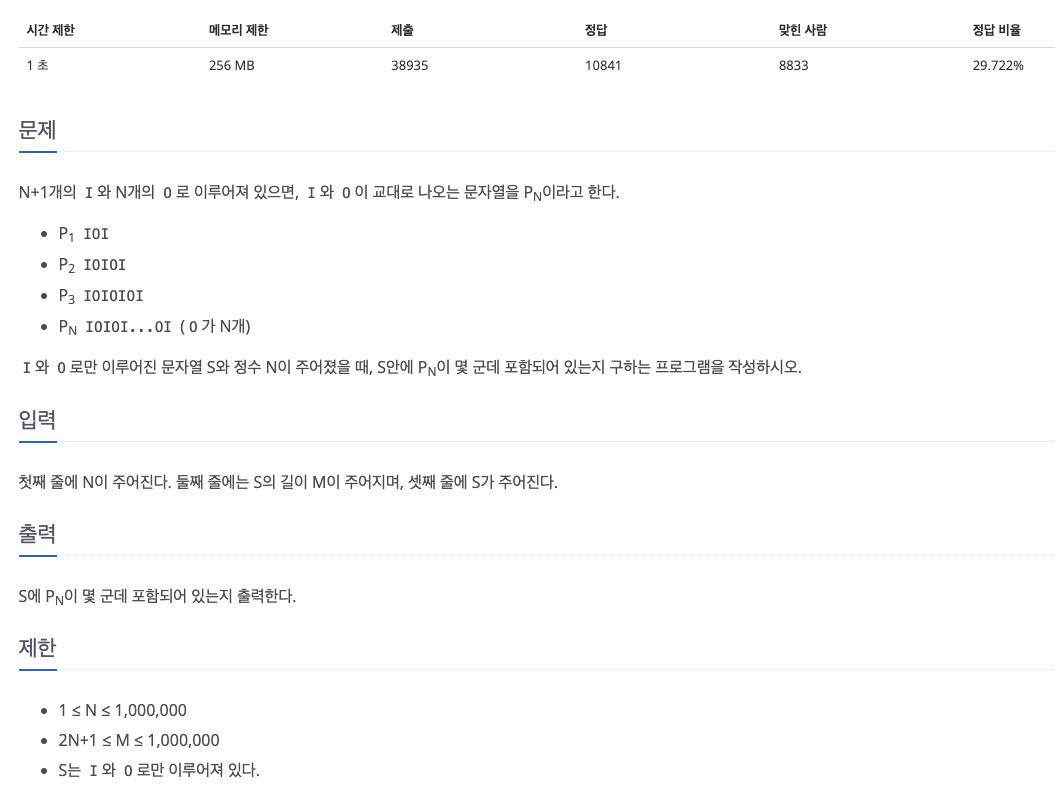
이 문제는 단순히 $P_N$을 구한 뒤, i번째 이후의 부분 문자열의 시작이 $P_N$인지 확인하면 정답이야 구할 수 있겠지만, 시간 복잡도가 $O(NM)$이므로 TLE가 발생한다.해서, 우리는 다른 풀이를 생각해야한다. 처음에는 KMP를 생각했으나, 해당 알고리즘에

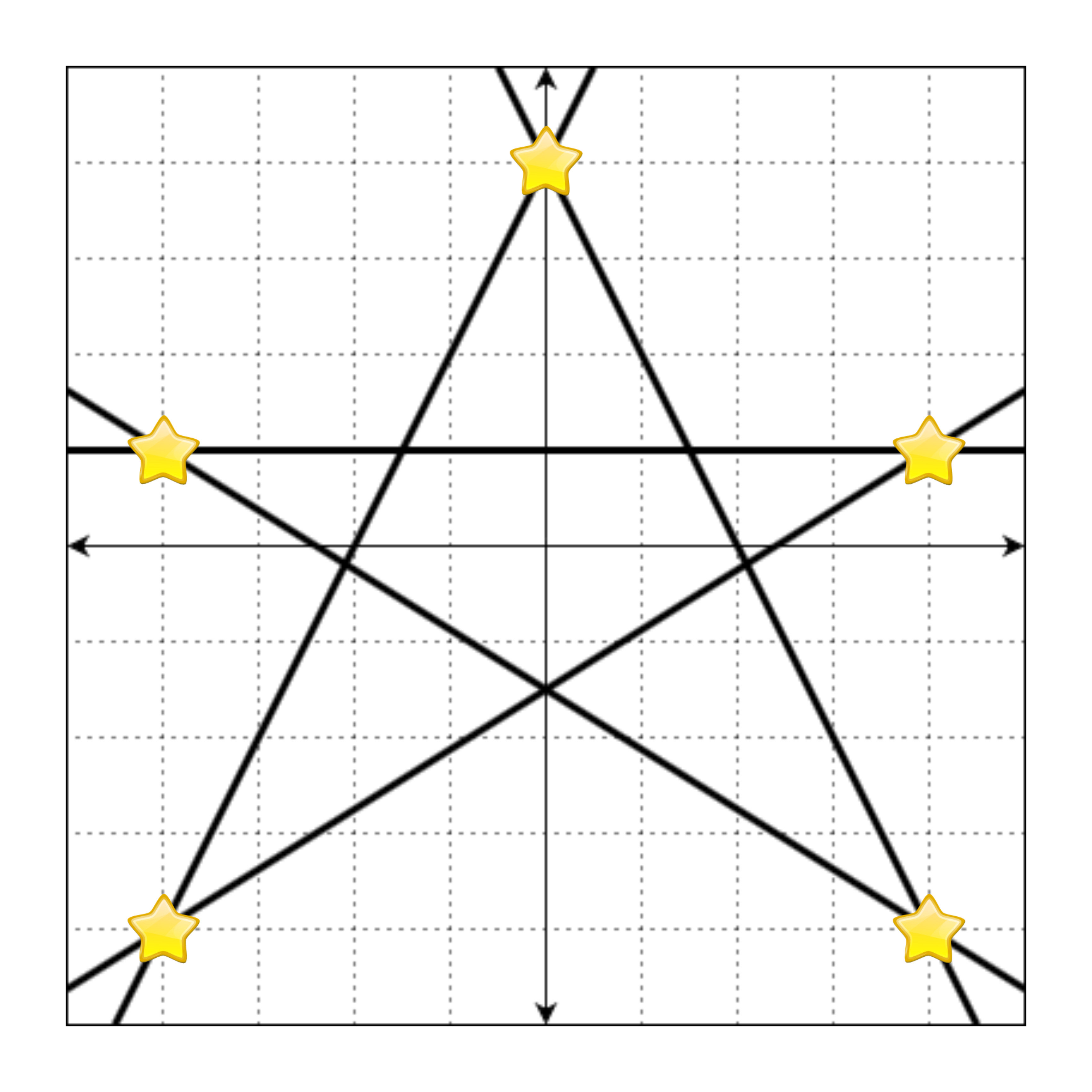
문제 링크: https://school.programmers.co.kr/learn/courses/30/lessons/87377Set<IntersectionPoint> points에 중복된 값을 가진 객체가 여러 개 들어가는 것을 방지하기 위해 Inters

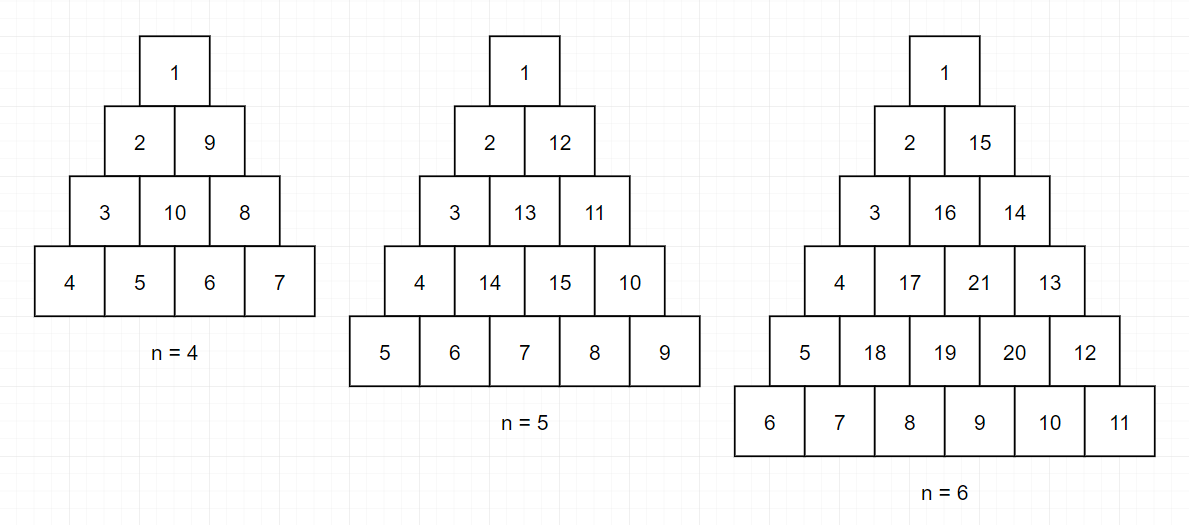
문제 링크: https://school.programmers.co.kr/learn/courses/30/lessons/68645문제 풀이 흐름$N \\times N$배열 선언숫자를 채울 현재 위치를 (0, 0)으로 지정방향에 따라 이동할 수 없을때 까지 반복하며

문제 링크: https://school.programmers.co.kr/learn/courses/30/lessons/81302참가자들이 맨해튼 거리가 2이하로 착석할 수 없지만, 파티션으로 격리되어 있다면 맨해튼 거리가 2이하여도 허용된다.이는 특정 칸으로부터

이 문제는 모든 정점에 대해 다른 정점으로의 최소 비용을 구하는 문제이다. 즉, 플로이드 워셜을 통해 문제를 해결할 수 있다.플로이드 워셜 알고리즘은 그래프가 주어져있을 때, 정점 s에서 정점 t로의 최소 비용 d\[s]\[t]는 min(d\[s]\[t], d\[s]\

이 문제는 플로이드 워셜 알고리즘으로 한 정점에서 다른 정점으로의 최소 비용을 구하고 경로 복원을 해야하는 문제이다.먼저, w\[s]\[t]는 s에서 t로의 최소 비용을 저장하고, nxt\[s]\[t]는 s에서 t로의 최소 비용이 되도록 하기 위해서 방문해야하는 다음

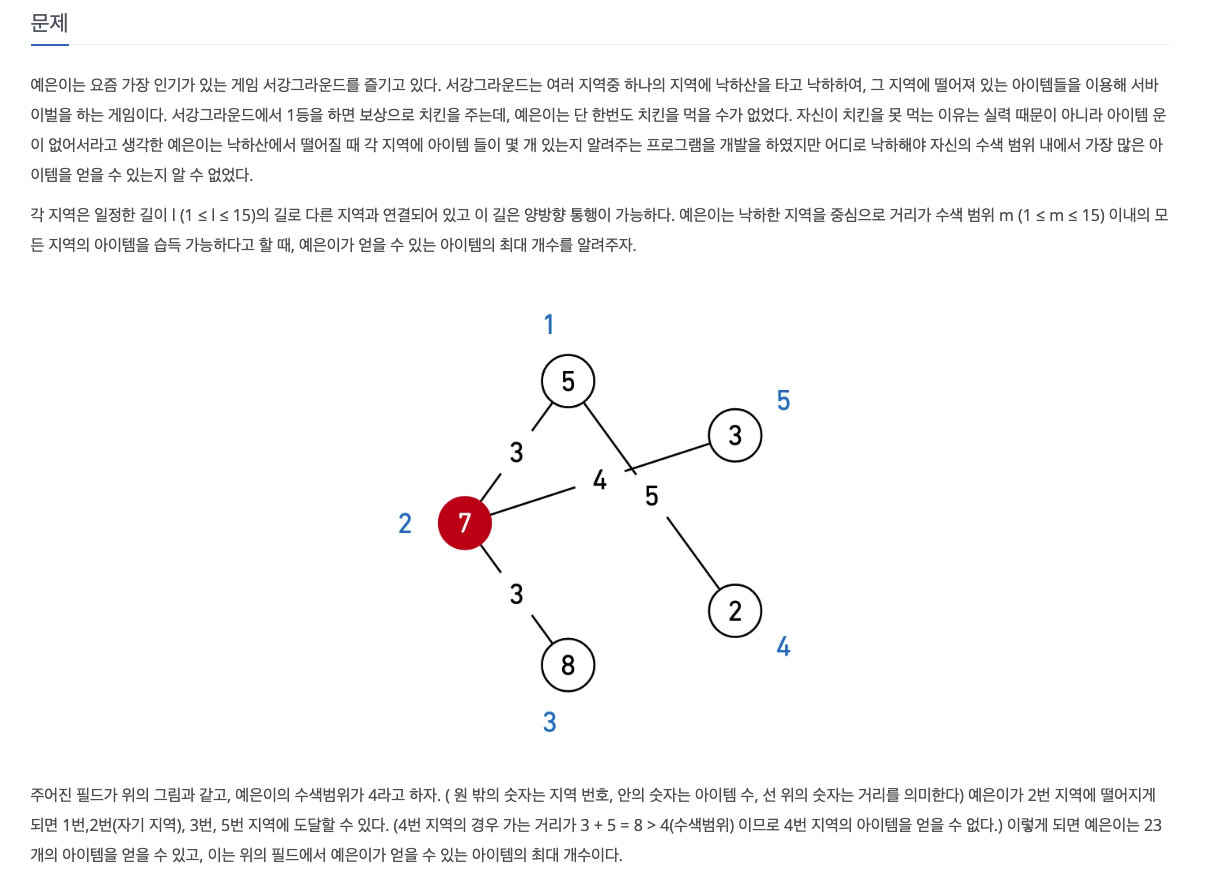
이 문제는 낙하한 지역을 중심으로 수색 범위 m이내의 모든 지역의 아이템을 습득 가능할 때, 예은이가 얻을 수 있는 아이템의 최대 개수를 구해야 한다.먼저, 낙하 지점을 선택해야하며, 낙하 지점에서 다른 지역으로의 최단 경로가 수색 범위 이내인지 확인한 뒤, 얻을 수

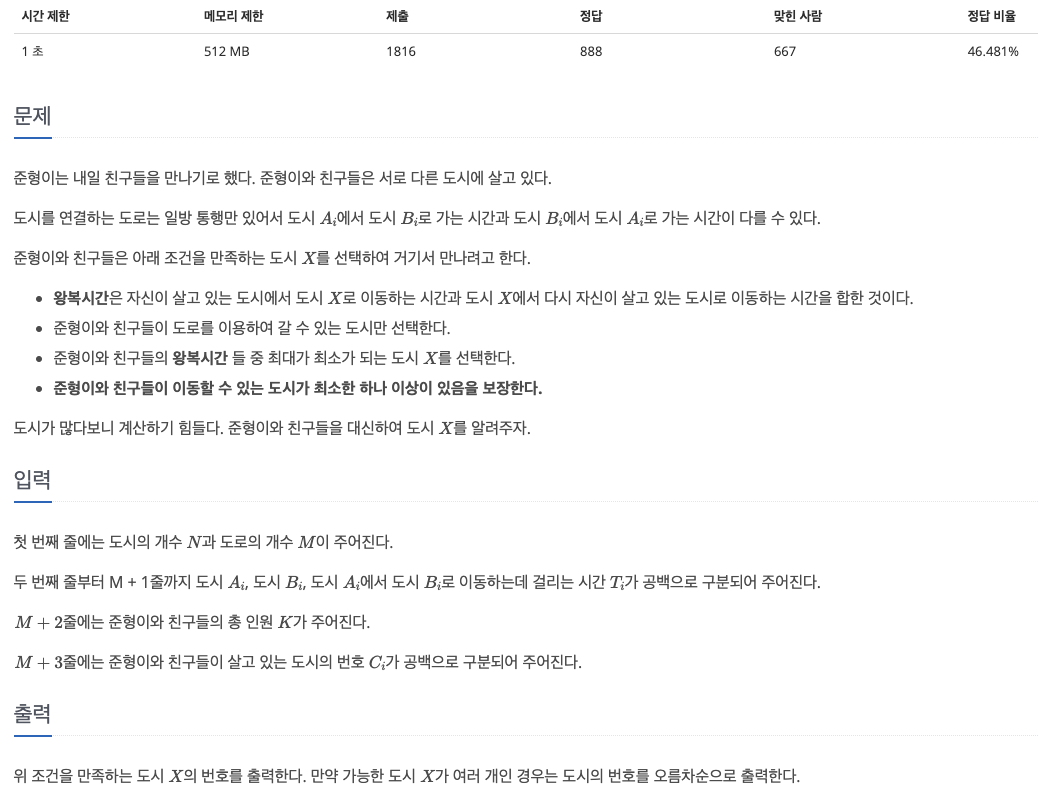
이 문제는 친구들의 왕복시간들 중 최대가 최소가 되는 도시 $X$를 선택하는 문제이다. 따라서, 왕복시간을 구하기 위해, 도시간 이동 시간(비용)을 구해야 하는데, 일반적으로 최소 비용이 이동 비용이 된다. 수학에서 거리를 규정하는 것과 같은 맥락이라 보면 된다. 즉,

이 문제는 도로의 길이의 합이 가장 작은 사이클을 찾는 문제이다. 이때, 사이클을 이루는 도로의 길이 합이 최소가 되려면 도로의 길이 자체가 최소가 되어야 한다. 따라서, 각 정점사이의 최단 경로를 구해야하므로 플로이드 워셜 알고리즘으로 접근해야 한다.그런데, 이 문제

이 문제는 길 정보가 주어졌을 때, s에서 e까지 가기 위해 최소 몇 개의 길을 양방향으로 바꿔야만 하는지를 구하는 문제이다.나는 처음에 브루트포스로 풀 수 있는지 고려해봤다. 최악의 경우는 모든 길이 단방향으로 주어진 경우이므로 최대 $\\frac {250 \\tim

이 문제는 Flood Fill 문제인 것이 쉽게 드러난다. 따라서, BFS나 DFS로 접근하면 문제를 해결할 수 있을 것이다. 필자는 편의상 BFS 풀이만 다룰 것이다.먼저, 모든 그림들에 대하여, Flood Fill로 넓이를 구하고, 최대 넓이를 갱신하는 방식으로 접

이 문제는 전형적인 BFS 문제이다. DFS로도 풀 수 있겠지만, 특정 위치에서 다른 위치로의 거리는 BFS로 접근하는 것이 더 편하기 때문에, BFS 풀이만 다루도록 할 것이다.먼저, 필자는 board배열의 (0, 0)부터 (n - 1, m - 1)에 미로를 저장할

이 문제는 근본적으로는 거리를 구하는 문제이다. 즉, 문제에서 주어진 익은 토마토로부터, 가장 멀리 떨어진 익지 않은 토마토까지의 거리를 구하면, 토마토가 익는데 걸리는 최소 날짜가 구해진다.따라서, 이 문제는 거리를 구하는 문제이므로 BFS로 접근하는 것이 좋아보인다

이 문제는 불이 났을 때, 지훈이가 가장 빨리 탈출할 수 있는 시간을 구하는 문제이다. 즉, 최단 탈출로의 길이를 구하는 문제라 할 수 있다.하지만, 문제에서 지훈이는 벽인 곳과 불이 난 곳은 방문할 수 없다고 명시되어 있으므로 이를 고려해야 한다.둘을 동시에 생각하는

이 문제는 저번에 다뤘던 토마토 문제의 변형이다. 따라서, 익은 토마토의 근처부터 차례로 익어가므로 BFS 알고리즘으로 접근해야한다.다만, 3차원이 되며 방향이 6개로 되었다는 점을 유의하며 접근해야 한다는 것을 잊지 말자.따라서, 인접 위치를 구하려면 dx, dy,

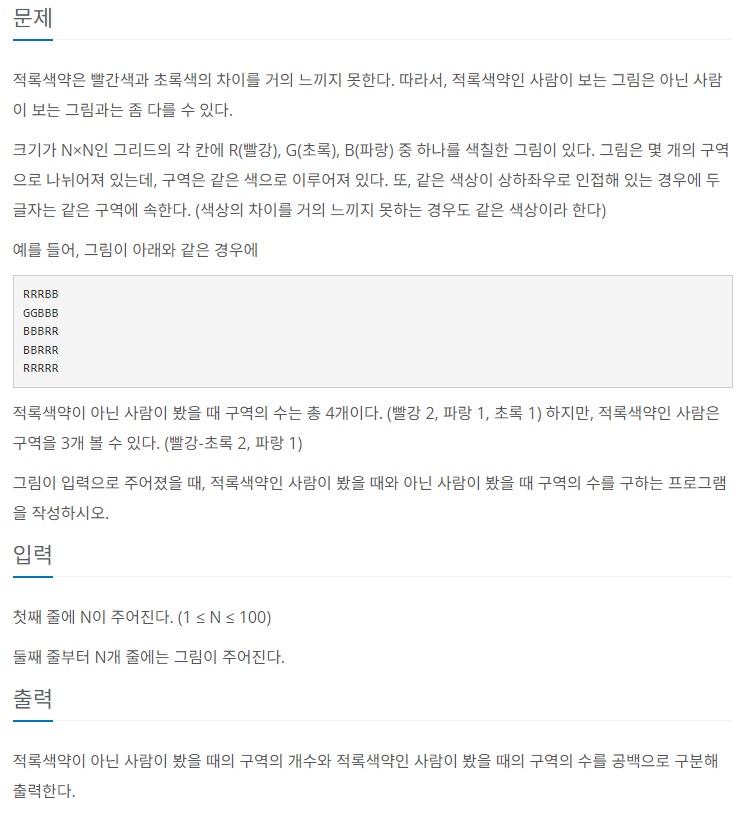
이 문제는 적록색약인 사람과 아닌 사람이 봤을 때, 색깔 영역의 갯수를 세는 문제로 전형적인 Flood Fill 문제이다. 따라서, BFS 알고리즘으로 접근하면 문제가 쉬워진다.그리고, 적록색약인 사람은 R과 G를 구별하지 못해 하나의 색으로 인식하지만, 그렇지 않은

이 문제는 나이트를 처음 위치에서 목표 위치로 이동시킬 때, 몇 번 이동해야하는지 계산하는 문제이다. 가장 단순한 방법은 처음부터 가능한 모든 경우를 따져보는 것이다. 이 문제에서는 $l^2$개의 체스칸이 존재하므로 가능한 조합을 모두 따지는 경우 $$

이 문제 역시 저번에 다루었던 백준 4179번 불!과 비슷한 문제이다. 다만, 테스트 케이스 여러 개가 주어진다는 점만 차이가 있다.불이 매초 사방으로 번져나가고, 상근이가 건물을 탈출하려하는 상황이다. 이때, 최단 탈출 경로를 구하는 문제로, 불이 번지는 것을 구하려

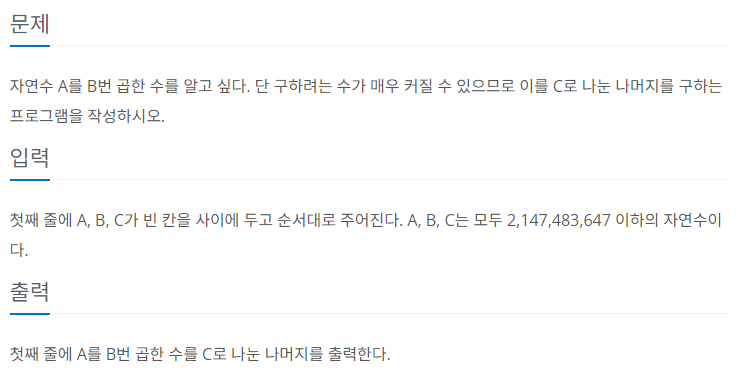
이 문제는 단순히 누적해 곱해나가는 방식으로는 시간초과가 발생한다. 이유는 컴퓨터는 대략 1초에 3~5억번의 연산이 가능한데 (다만, 보수적으로 잡으면 1억번) 최악의 경우 곱셈만 20억번 넘게 하게되므로 무조건 시간초과가 발생하는 것이다.따라서, $O(N)$의 시간복

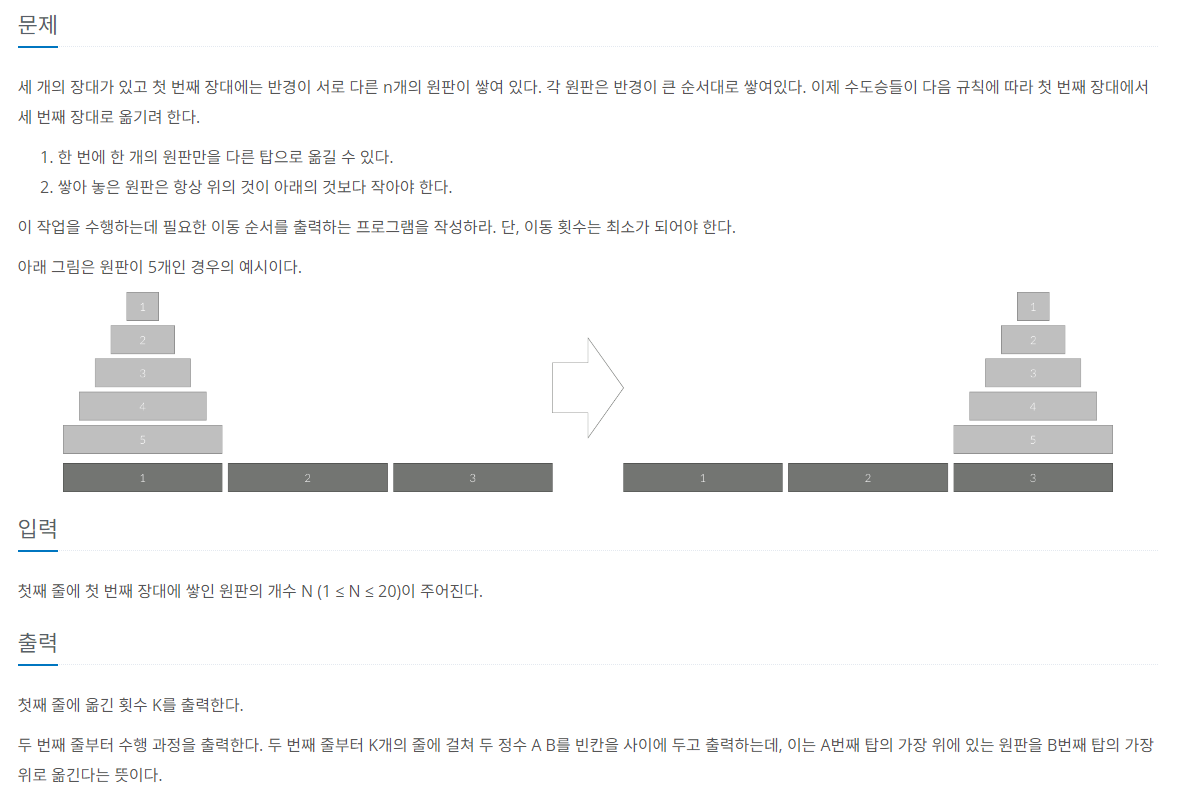
하노이탑은 진짜 웰논이다... 위의 그림처럼 원판 5개가 놓여있으면 위에 있는 4개 원판을 2번 기둥에 옮겨야한다. 이는 원판 4개인 경우의 하노이탑과 굉장히 유사하다. N개의 원판을 현재 기둥에서 다른 기둥으로 옮길 때, 하노이탑 규칙을 준수하며 옮기기 때문이다.따라

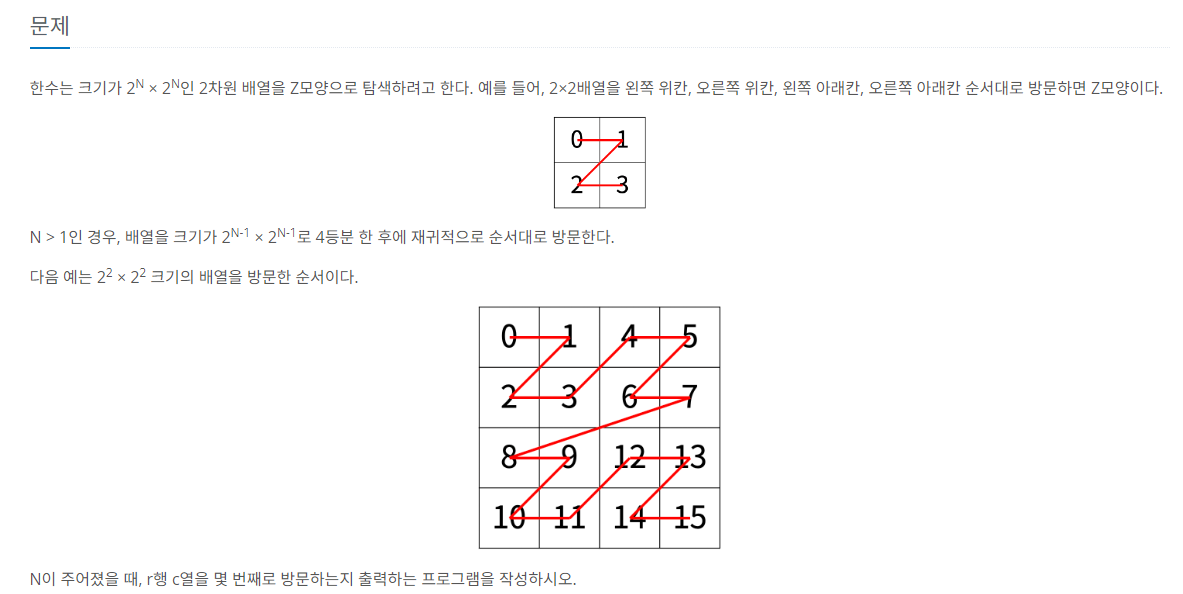
이 문제는 $N \\le 15$, $0 \\le r, c \\lt 2^N$이므로, 모든 칸의 방문 순서를 구한다면 최악의 경우 $2^{30} \\approx 10^9$이므로 시간초과가 발생한다.따라서, r행 c열의 방문 순서를 직접 구해야하는데, 이는 반복해서 배열을

이 문제는 종이를 반복적으로 분할해나가며, 해당 섹션에 적힌 숫자가 모두 같은지 확인해야하는 문제이다.따라서, 섹션을 확인하는 과정과 섹션을 분할하는 과정이 필요할 것이다.그리고, 섹션에 적힌 숫자가 모두 일치하지 않다면, 섹션을 9등분하여 다시 확인해야하므로 재귀임이

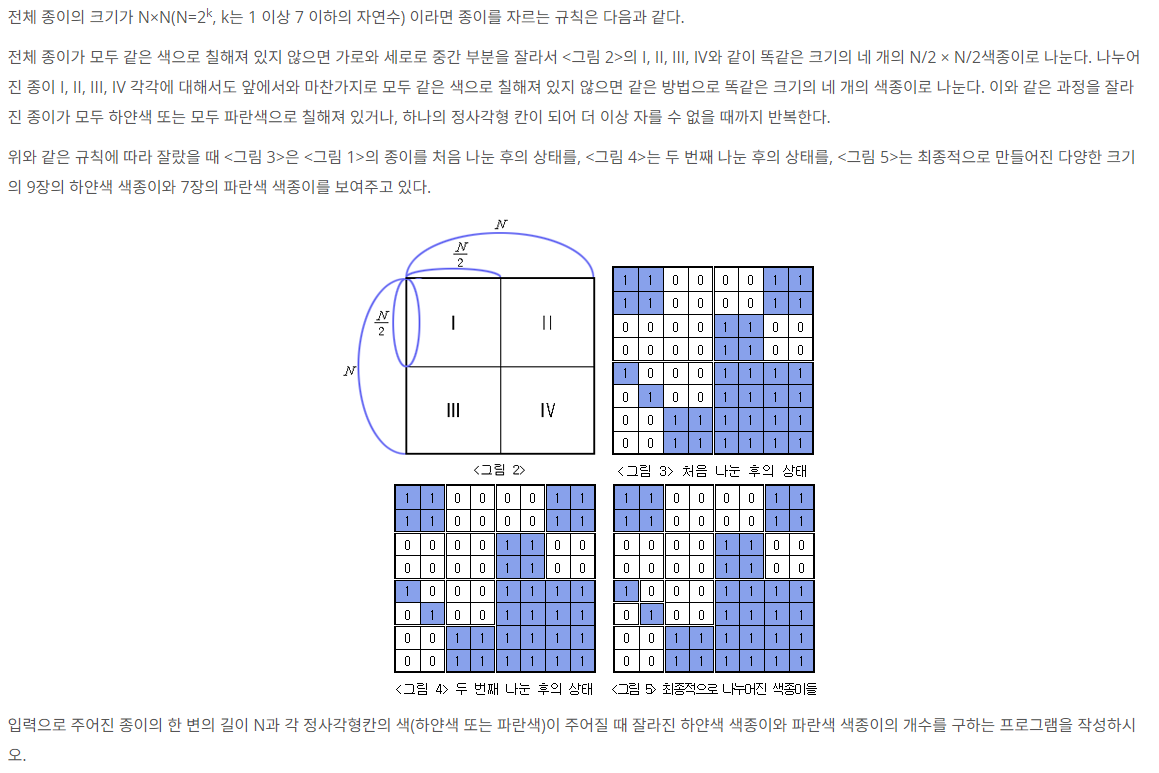
이 문제는 직전에 풀었던 종이의 개수와 비슷한 문제이다.모두 같은 색인지 확인한 뒤, 같다면 해당 색깔의 종이 갯수를 1 증가시키고, 그렇지 않다면 4분할하여 같은 과정을 반복해나가면된다.따라서, 백준 1780번(종이의 개수)와 굉장히 유사하다는 것을 알 수 있다.여기

이 문제는 막대에 꽂혀있는 과일들이 주어졌을 때, 앞과 뒤에서 임의의 개수만큼 제거하여 막대에 꽂혀있는 과일의 개수가 2개 이하가 되는 경우 중, 과일의 최대 개수를 구하는 문제이다.처음에는 앞과 뒤에서 과일을 제거한다길래, Deque을 생각했는데 이 경우 문제가 너무

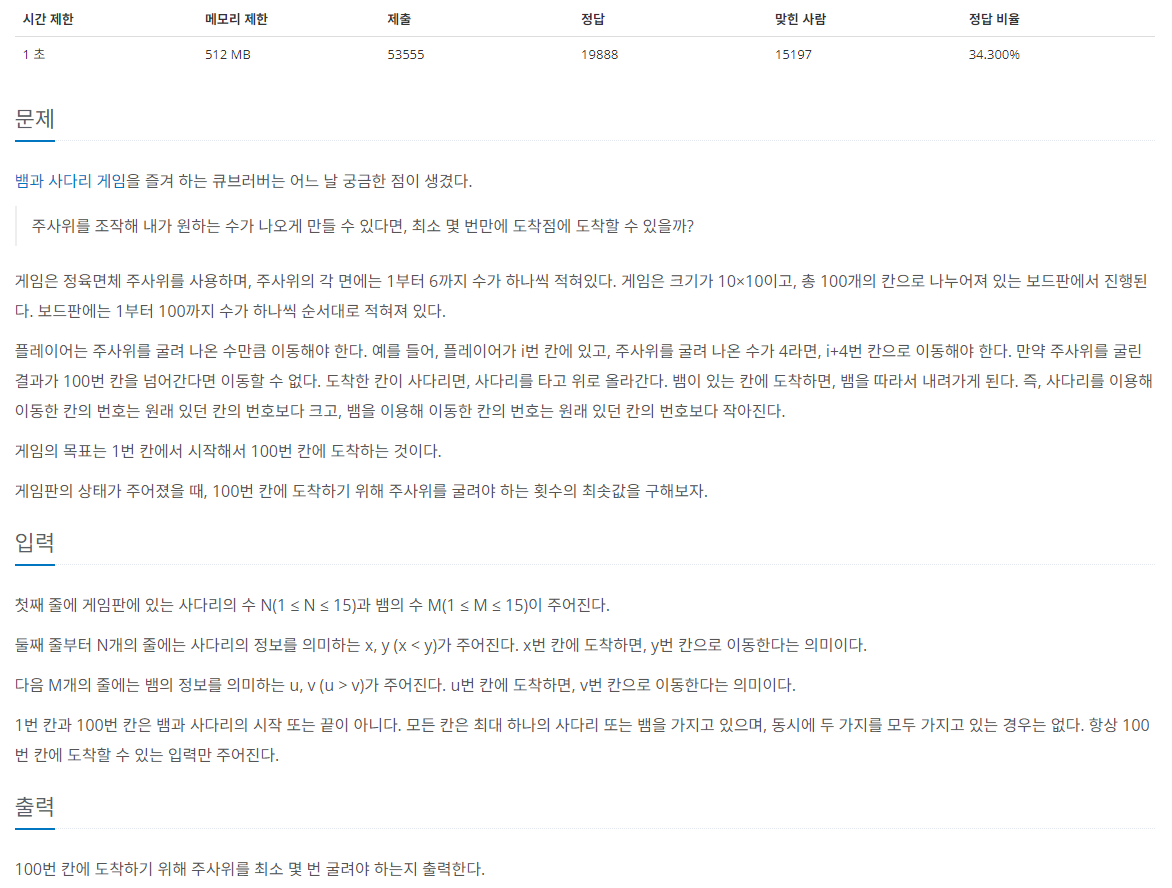
이 문제는 주사위를 굴려 나온 눈만큼 칸을 이동하며, 뱀이 나오면 더 큰 수가 적인 칸으로 이동하고, 사다리가 나오면 더 작은 수가 적힌 칸으로 이동하는 게임이다. 이때, 100번 칸에 도착하기 위해 주사위를 최소 몇 번 굴려야 하는지를 구하는 문제이다.문제 조건에서,

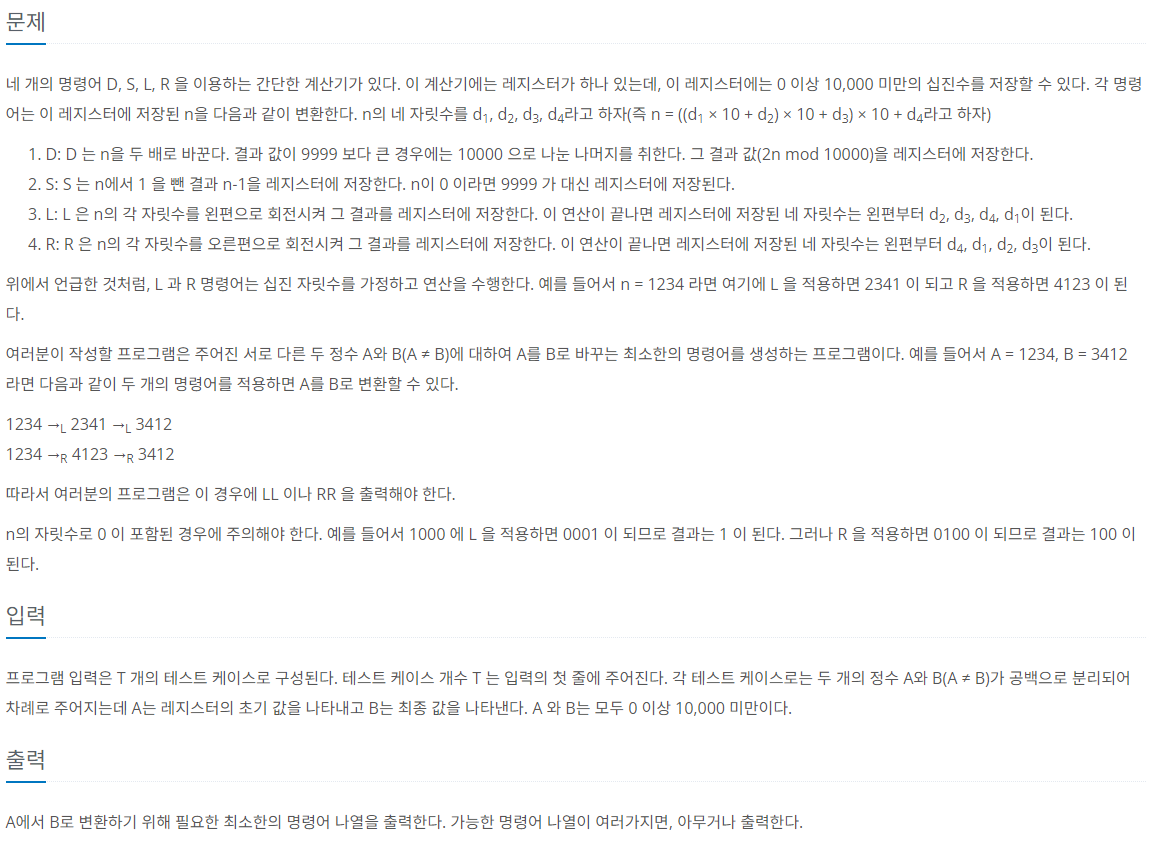
이 문제는 시간 제한이 6초로 널널하다. 그래서 모든 경우를 따져보면 될 것 같다. 하지만, 모든 경우를 따지면 시간복잡도가 $$O(N^4)$$가 되므로 시간초과가 발생한다.문제에서 명령어가 여러가지이면 아무거나 출력하라고 했으므로, BFS로 최단 경로로 접근하되 방문

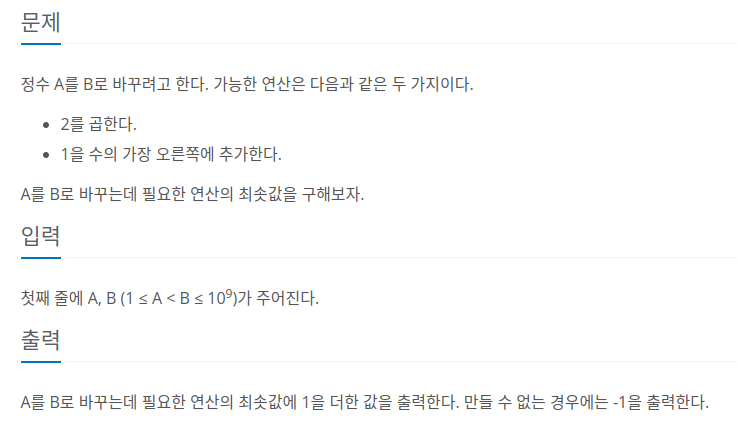
이 문제는 정수 A를 B로 바꾸는데 필요한 연산의 최소값을 구하는 문제이다. 얼핏보면, DP를 활용하여 문제를 해결할 수 있을 것 같지만, 이는 잘못된 생각이다. 왜냐하면 A와 B의 범위가 $$10^9$$이하이기 때문에, 시간복잡도가 $$O(N)$$의 형태인 DP에서는

이 문제는 문자열 s가 주어졌을 때, s에서 영문자나 숫자가 아닌 문자들을 제거하고 모든 문자를 소문자로 변경한 뒤, 이 문자열이 팰린드롬인지 판단하는 문제이다.정말 단순하게 s.toLowerCase().replaceAll("\[^a-z0-9]", "")로 문제의 요구

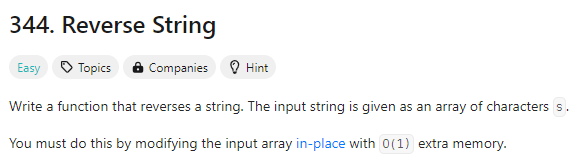
이 문제는 배열 내부에서 문자열을 뒤집는 문제이다.이는 정말 간단하게 투포인터로 풀어낼 수 있다. 한 포인터는 0부터 오른쪽으로, 다른 포인터는 끝 위치에서부터 왼쪽으로 이동해가며, 두 포인터가 각각 가리키는 위치의 원소들을 swap해주면 되는 문제이다.이를 코드로 옮

이 문제는 문자열 배열인 logs가 주어졌을 때, logs를 조건에 맞게 재정렬하는 문제이다.이 때, 문자 로그와 숫자 로그의 정렬 방식이 상이함을 알 수 있다.따라서 문자 로그와 숫자 로그를 분리한 뒤, 각각 정렬한 뒤 둘을 연결하여 해결하는 것이 유리할 것이다.먼저

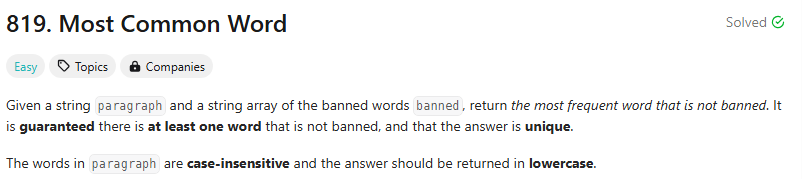
이 문제는 paragraph와 금지 단어들이 문자열 배열 banned로 주어질 때, 금지되지 않은 단어들 중 최빈 단어를 찾는 문제이다.먼저, paragraph에서 단어들을 추출해야한다.따라서 split을 해야하는데, paragraph에는 대소문자 뿐만 아니라 쉼표,

풀이 이 문제는 문자열 배열 strs가 주어졌을 때, 애너그램들끼리 그룹으로 묶어 리턴하는 문제이다. 애너그램이란, 단어(word)나 구(phrase)가 주어져있을 때, 문자를 재배열해서 만들어지는 새로운 단어나 구를 말한다. 따라서, 애너그램들은 각 문자들의 개

이 문제는 문자열 s가 주어졌을 때, s안의 가장 긴 팰린드롬 부분 문자열을 구하는 문제이다.정말 단순히 생각하자면 부분 문자열을 정한 뒤, 팰린드롬인지 판단하면 될 것 같다. 이 풀이는 시간복잡도가 $$O(N^2)$$으로, 문제 조건인 $$1 \\le N \\le 1

https://leetcode.com/problems/two-sum/description/이 문제는 정수 배열 nums와 정수 target이 주어졌을 때, nums의 두 원소들의 합이 target이 되는 원소들의 인덱스들을 리턴하는 문제이다.가장 먼저, 가능한

https://leetcode.com/problems/trapping-rain-water/이 문제는 각 막대의 너비가 1인 고도지도에서 높이를 나타내는 음수가 아닌 정수 n들이 주어질 때, 얼마나 많은 물이 비가 온 뒤 갇히는지 계산하는 문제이다.물이 갇히려면

https://leetcode.com/problems/3sum/description/?page=1&search=332이 문제는 정수 배열 nums가 주어졌을 때, 세 수의 합이 0이 되는 묶음을 모두 반환하는 문제이다.먼저, 브루트포스로 풀이할 생각을 할 수

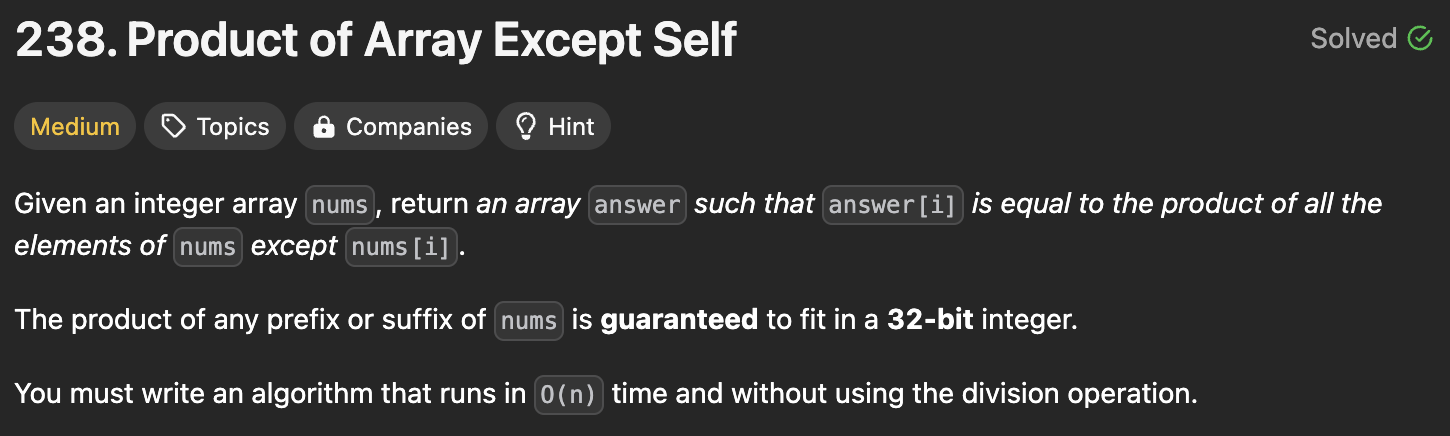
https://leetcode.com/problems/product-of-array-except-self/description/?page=1&search=332이 문제는 정수 배열 nums가 주어졌을 때, i번째 인덱스의 값이 nums\[i]를 제외한 나머지