[백준 15681] 트리와 쿼리 (C++)

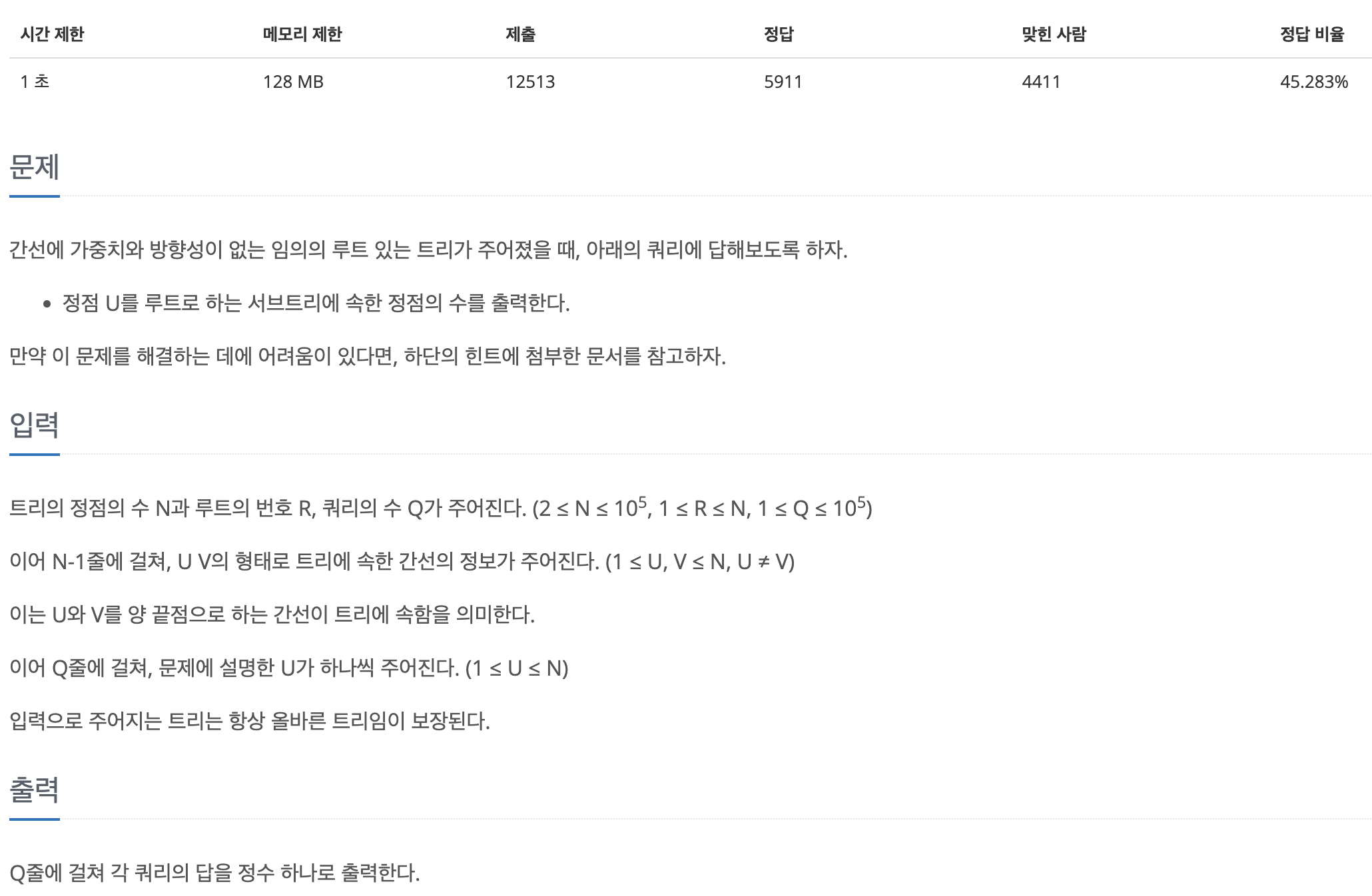
이 문제는 정점들의 연결관계를 통해 트리 정보가 주어진 후, 정점이 쿼리로 들어오는데, 해당 정점을 루트로 하는 서브 트리의 정점 갯수를 출력하는 문제이다.

정점들의 연결관계로 트리가 표현되기 때문에, 인접 행렬이나 인접 리스트를 사용해 트리를 표현해야 한다. 하지만, 공간복잡도가 $O(V^2)$인 인접 행렬은 $V \le 10^5$이므로 메모리 초과가 발생한다. 따라서, 공간복잡도가 $O(V + E)$인 인접 리스트로만 트리를 표현할 수 있다.

이제, 트리에서 서브 트리에 속한 정점들을 탐색해야 한다.
우리는 정점이 쿼리로 주어질 때마다, 해당 정점에서 탐색하는 방법을 생각할 수 있다.

이는, 시간복잡도가 $O(Q(V+E))$가 되므로, 시간 초과가 발생한다.

따라서, 매 번 트리를 탐색하는 것이 아니라, 미리 서브트리에 속하는 정점 갯수를 구해두고 쿼리가 들어올 때, 값을 출력해주도록 하는 방법을 고려해보자.

트리를 탐색할 때 BFS로 탐색한다면, 자식이 몇 개인지 파악하기 쉽지 않다. 따라서, 이는 적절한 방법이 아니다.

만약, DFS로 탐색한다면, 서브트리를 방문하고 부모로 돌아오는 과정을 반복한다.

이 과정에서, 서브 트리를 먼저 방문했기 때문에, 서브 트리에 속하는 정점의 갯수를 손쉽게 구할 수 있다. 이후, 루트 노드까지 추가해주면 해당 트리에 속하는 모든 노드의 갯수를 파악할 수 있다.

이렇게 구현하려면, 서브 트리를 방문했다가 부모로 재방문을 해야하는데, 이는 재귀 DFS로 손쉽게 구현이 가능하다.

#include <bits/stdc++.h>
using namespace std;

int n, r, q;
vector<int> adj[100'001];
int p[100'001], cnt[100'001];

void dfs(int cur) {
	cnt[cur]++;
	for (int nxt : adj[cur]) {
		if (p[cur] == nxt) continue;
		p[nxt] = cur;
		dfs(nxt);
		cnt[cur] += cnt[nxt];
	}
}

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);

	cin >> n >> r >> q;
	for (int i = 0, u, v; i < n - 1; i++) {
		cin >> u >> v;
		adj[u].push_back(v);
		adj[v].push_back(u);
	}

	dfs(r);

	while (q--) {
		int u;
		cin >> u;
		cout << cnt[u] << "\n";
	}
}