[백준 1707] 이분 그래프 (C++)

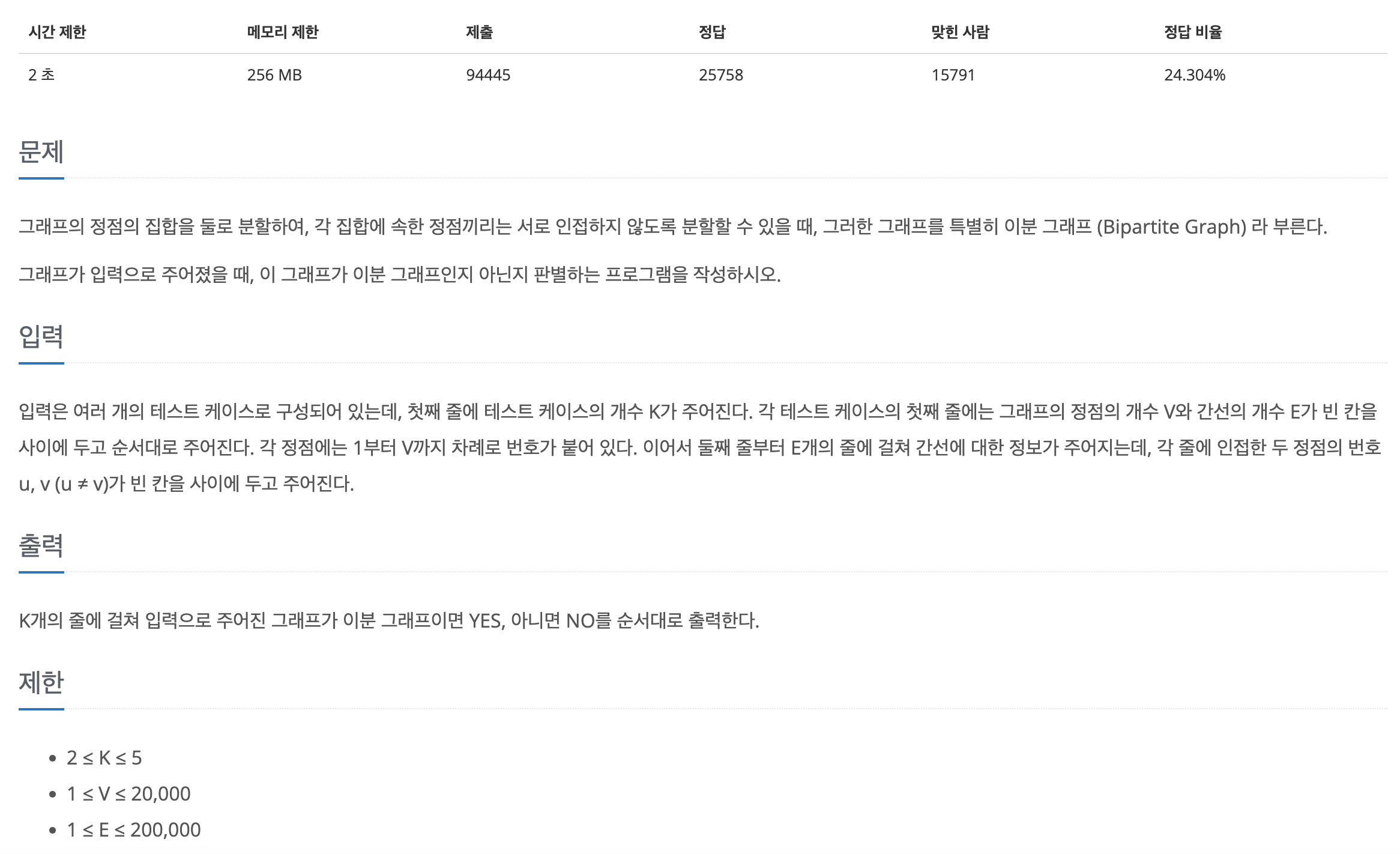
주어진 그래프가 이분 그래프인지 판별하는 문제이다.

이 문제는 그래프 표현시 인접 행렬로 표현하면 공간복잡도가 $O(V^2)$으로 메모리 초과가 나는 문제이다. 따라서, 공간복잡도가 $O(V + E)$인 인접 리스트로 표현해야 한다.

이분 그래프란, 인접한 정접을 서로 다른 색으로 칠해서 2가지의 색으로만 칠할 수 있는 그래프를 이분 그래프라 한다.

즉, 인접한 정점에 색을 칠해야하므로 BFS로 접근해야 하고, 색을 편의상 $0$과 $1$로 표현하자. 현재 정점의 색을 vis[cur]라 할 때, 인접 정점의 색 vis[nxt]은 (vis[cur] + 1) % 2가 된다.

만약, 방문한 적이 있는 정점이 인접 정점이라면, 색이 동일한지 체크하면 된다.
색이 동일하다면 이분 그래프가 아닌 것을 곧바로 알 수 있다.
모든 정점에서 색이 동일하지 않다면 이분 그래프임을 알 수 있다.

이를 코드로 옮기면 다음과 같다.

#include <bits/stdc++.h>
using namespace std;

int k, V, E;
vector<int> adj[20'001];

bool bfs() {
	queue<int> q;
	vector<int> vis(V + 1, -1);
	for (int i = 1; i <= V; i++) {
		if (vis[i] != -1) continue;
		q.push(i);
		vis[i] = 0;

		while (!q.empty()) {
			int cur = q.front();
			q.pop();

			for (int nxt : adj[cur]) {
				if (vis[nxt] != -1) {
					if (vis[nxt] == vis[cur]) return 0;
					continue;
				}
				q.push(nxt);
				vis[nxt] = (vis[cur] + 1) % 2;
			}
		}
	}

	return 1;
}

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);

	cin >> k;
	while (k--) {
		cin >> V >> E;
		for (int i = 1; i <= V; i++) adj[i].clear();

		for (int i = 0; i < E; i++) {
			int u, v;
			cin >> u >> v;
			adj[u].push_back(v);
			adj[v].push_back(u);
		}

		cout << (bfs() ? "YES" : "NO") << "\n";
	}
}

추가로 bfs의 결과를 곧바로 YES와 NO를 주도록 리팩터링 하는 것도 좋아보인다.