[백준 1781] 컵라면 (C++)

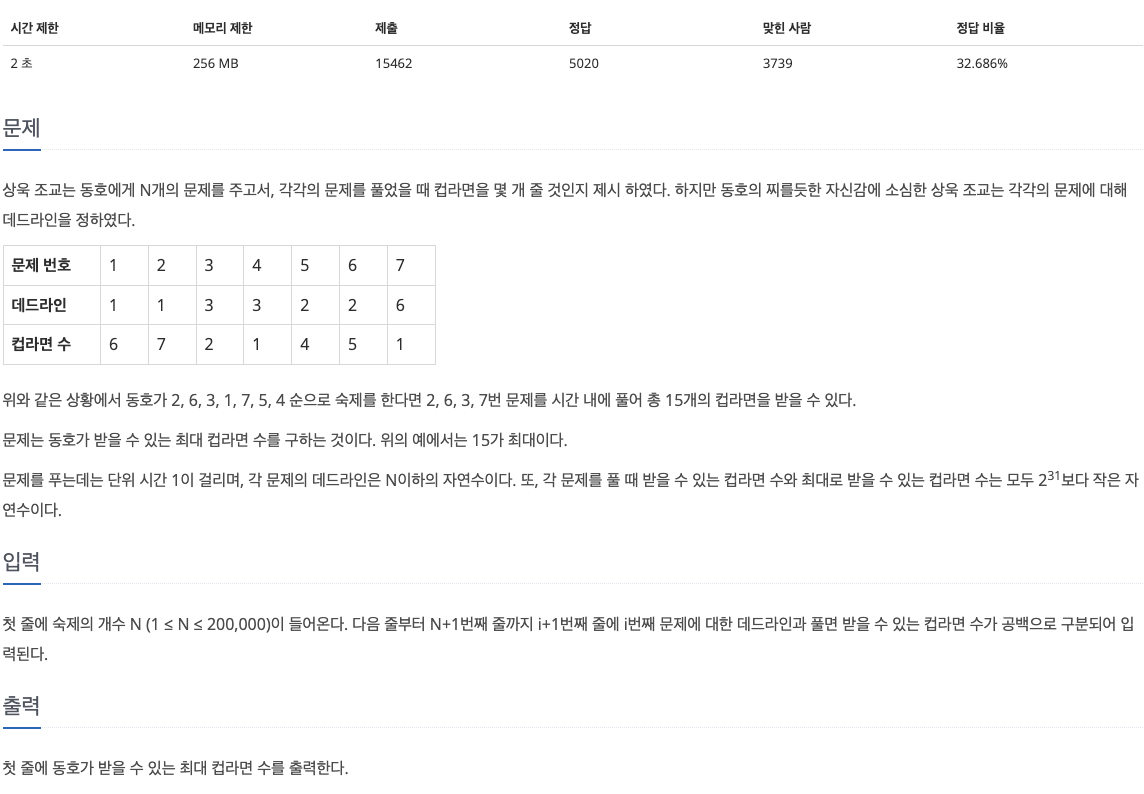
이 문제는 $N$개의 문제의 데드라인과 컵라면 수가 주어졌을 때, 동호가 받을 수 있는 최대 컵라면 수를 구하는 문제이다.
이는 데드라인 이내의 문제 중 컵라면을 가장 많이 주는 문제들을 골라 푸는 것으로 구할 수 있다.

추가로 문제를 푸는데 단위 시간 1이 걸린다고 했으니, 현재까지 푼 문제 수는 시간과 동일하게 될 것이고, 이보다 데드라인이 크거나 같아야 컵라면을 받을 수 있다. 그리고 이중 컵라면 수가 최대인 문제를 풀면 될 것이다.

이 문제에서 실수하기 좋은 것들은 같은 데드라인을 갖더라도 동호가 문제를 풀 수 있다는 것과 데드라인이 가장 가까운 것 중 컵라면을 최대로 주는 문제를 선택하는 것이다.

아래의 경우와 함께 실수하기 좋은 이유를 살펴보자.

4
1 1
2 1
3 10
3 10

데드라인이 가장 임박한 것들 중 컵라면 갯수가 최대인 문제를 선택한다고 가정하자.

그렇다면, 1,2,3번이 선택되어 1 + 1 + 10 = 12가 출력된다.

하지만, 1,3,4번을 선택하면 1 + 10 + 10 = 21이 되어 더 큰 값이 있다는 것을 알 수 있다.

무턱대고 데드라인을 오름차순으로 컵라면 갯수를 내림차순으로 정렬하고 선택해나가도록 하는 것은 최대를 보장할 수 없다는 것이다.

그리고, 데드라인이 동일해도 시점 $t_0$보다 같거나 크다면, 또 풀 수 있다는 것을 확인할 수 있다.

❗️ 따라서, 앞서 언급했듯이 데드라인 이내인 문제들 중 컵라면을 최대로 주는 문제를 선택해나가야 한다.

✅ 이제 자료구조에 대해 생각해보자.

이 문제는 $N \le 200,000$이므로 선형 자료구조로 데드라인과 컵라면을 관리하게 되면 시간 초과가 된다.

배열이나 연결 리스트는 각 시점 $t_0$에서 풀었을 때 컵라면을 받을 수 있는 문제들 중 받을 수 있는 컵라면 수가 최대인 문제를 고르는데 $O(N)$의 시간 복잡도가 필요하다. 따라서, 전체 시간 복잡도는 $O(N^2)$이므로 시간 초과가 된다.
추가로 이분 탐색으로 삽입할 위치를 찾는다고 해도 삽입 자체에서 $O(N)$의 시간 복잡도가 필요하니 이분 탐색을 적용해도 전체 시간 복잡도는 마찬가지로 $O(N^2)$가 된다.

그리고, 스택이나 큐를 monotone-stack으로 사용하는 방법인데, 각 문제마다 이를 유지하는데 시간복잡도가 $O(N)$이 필요하기 때문에, 전체 시간복잡도는 $O(N^2)$이 된다. 따라서, 시간 초과가 발생한다.

그렇기 때문에, 선형 자료구조로는 해결이 불가능하고 정렬 상태를 유지하면서 삽입과 삭제가 빈번히 일어나므로 트리 형태의 자료구조로 데이터를 저장해야 한다.

❗️ 하지만, 이 문제 상황에서는 우선순위가 가장 큰 것만 관심이 있으므로 우선순위 큐에 데이터를 저장하면 될 것이다.

그렇다면, 데드라인 이내의 문제들을 어떻게 $O(N)$이내로 알아낼 수 있을까?

이는 현재 시간이 $t$이고 문제의 데드라인을 $d_k$라고 가정하고 접근해보자.

이때, 우리는 $t \le d_k$를 만족하는 문제들을 살펴봐야 한다.$t$를 1부터 살펴본다면, 우선순위 큐에 {데드라인, 컵라면 수}의 형태로 원소들이 저장해야 하고, 매번 $d_k$이하의 시점에 문제를 풀었는지 체크해야한다. 즉, $1$ ~ $d_k$의 범위에서 문제를 풀지 않은 시점 $t_0$를 찾는 행위를 모든 문제에서 반복해야 한다는 것이고 전체 시간 복잡도는 $O(N^2)$이 될 것이다.

좀 더 구체적으로 설명하자면, $d_k$에 문제를 풀 수 있는지 먼저 확인해보고 해당 시점에 문제를 푼 적이 있으면 충돌이 일어났기 때문에 그 이전 시점들에서 처리가 가능한지 확인을 해야한다. 따라서 시간 복잡도는 $O(N^2)$이 된다.
(문제를 풀었는지 여부를 저장하는 배열은 정렬이 불가능하므로 이분 탐색을 진행할 수 없다.)

이 상황을 코드로 구현해보면 다음과 같이 된다는 의미이다. (이 코드는 시간 초과가 난다는 것을 참고하자.)

#include <bits/stdc++.h>
#define X first
#define Y second
using namespace std;

class Compare {
 public:
  bool operator()(const pair<int, int> &a, const pair<int, int> &b) {
	  if (a.Y != b.Y) return a.Y < b.Y;
	  return a.X > b.X;
  }
};

int n, ans;
int solve[200'001];
priority_queue<pair<int, int>, vector<pair<int, int>>, Compare> pq;

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);
	
	cin >> n;
	for (int i = 0, d, c; i < n; i++) {
		cin >> d >> c;
		pq.push({d, c});
	}

	while (!pq.empty()) {
		for (int i = pq.top().X; i > 0; i--) {
			if (solve[i]) continue;
			solve[i] = pq.top().Y;
			break;
		}
		pq.pop();
	}

	for (int i = 1; i <= n; i++) ans += mx[i];
	cout << ans;
}

하지만, 관점을 바꾸어 가장 나중에 처리될 것 부터 결정하게 된다면, 문제의 데드라인이 넘지 않았음을 굳이 확인해보지 않더라도 보장할 수 있다.

구체적으로, 문제들을 데드라인 별로 묶어서 관리한다는 의미이다. 이 문제 상황에서는 문제 번호는 의미가 없으므로 데드라인 별로 컵라면 수를 묶어서 관리하는 꼴이 된다. 이는 $N \le 200,000$이므로 vector<int> cnt[200'001]으로 표현이 가능하고, 각각의 cnt[d]에는 데드라인 $d$에 대한 컵라면 수들이 리스트로 관리된다는 의미이다.

이때 관점을 바꾸어, 시점 $t$를 데드라인의 최댓값인 $N$부터 $1$까지 역순으로 결정한다면, $t \le d$를 만족하는 데드라인 $d$의 범위는 $t \le d \le N$가 된다.

데드라인 $d$를 $N$부터 역순으로 cnt[d]의 리스트를 우선순위 큐 pq에 저장해 두면 시점 $t$에서는 우선순위 큐에 $t \le d$인 문제들만이 남게 된다. 따라서, 다음과 같이 코드를 구성해 볼 수 있다.

for (int i = n; i > 0; i--) {
	for (int c : cnt[i]) pq.push(c);
	if (pq.empty()) continue;
	ans += pq.top();
	pq.pop();
}

✅ 전체 코드는 다음과 같다.

#include <bits/stdc++.h>
using namespace std;

int n, ans;
vector<vector<int>> cnt(200'001);
priority_queue<int> pq;

int main() {
	ios::sync_with_stdio(0);
	cin.tie(0);

	cin >> n;
	for (int i = 0, d, c; i < n; i++) {
		cin >> d >> c;
		cnt[d].push_back(c);
	}

	for (int i = n; i > 0; i--) {
		for (int c : cnt[i]) pq.push(c);
		if (pq.empty()) continue;
		ans += pq.top();
		pq.pop();
	}
	cout << ans;
}