1. 기본적인 정렬 알고리즘

1. 선택 정렬 (Selection Sort)

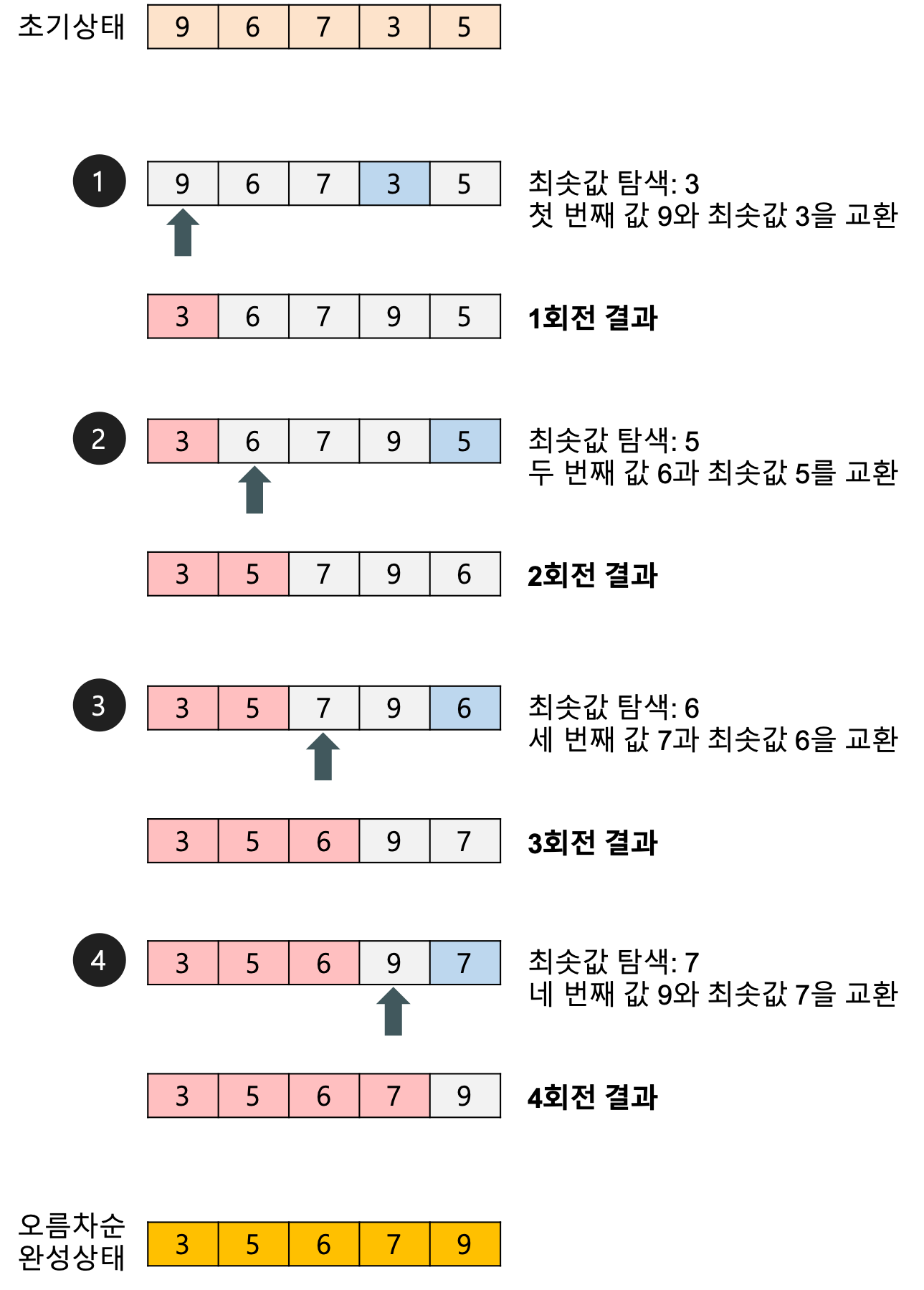
1. 주어진 리스트에서 최솟값을 찾는다.
2. 최솟값을 맨 처음의 index값과 위치 변경을 한다.
3. 맨 처음의 index값을 제외한 나머지 값들 중 최솟값을 찾아 위와 같은 방법으로 반복한다.

public class Main {
    public static void main(String[] args) {
        int[] a = {9,6,7,3,5};
        selection_sort(a, a.length);
        
        for(int i = 0; i < a.length ; i ++) {
            System.out.println(a[i]);
        }
    }
    private static void selection_sort(int[] a, int length) {

        for(int i = 0; i < length - 1; i++) {
            int min_index = i;

            // 최솟값을 갖고있는 인덱스 찾기
            for(int j = i + 1; j < length; j++) {
                if(a[j] < a[min_index]) {
                    min_index = j;
                }
            }
            // i번째 값과 찾은 최솟값을 서로 교환
            swap(a, min_index, i);
        }
    }
    private static void swap(int[] a, int i, int j) {
        int temp = a[i];
        a[i] = a[j];
        a[j] = temp;
    }
}

전체 코드는 위와 같이 됩니다. 아래의 코드에 대해서 좀 더 알아보겠습니다.

for(int i = 0; i < length - 1; i++) {
	System.out.println(i);
	int min_index = i;
	// 최솟값을 갖고있는 인덱스 찾기
	for(int j = i + 1; j < length; j++) {
		if(a[j] < a[min_index]) {
			min_index = j;
		}
	}
	// i번째 값과 찾은 최솟값을 서로 교환
	swap(a, min_index, i);
}

배열의 길이를 위의 for문 경우는 length-1 아래 for문 length 까지 합니다. 그 이유는 1 2 3 4 5 가 있다면 비교하는 값으로 최소값은 4까지만 구하면 다음 값에서 +1를 해서 5의 인덱스를 가져와서 비교해서 정렬을 하기 때문입니다. 그래서 배열의 갯수가 1개더 적은 부분까지만 서치를 해도 됩니다.

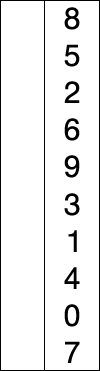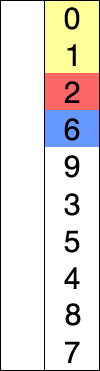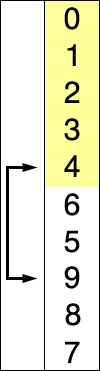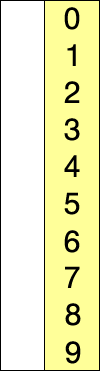
위 그림을 통해서 쉽게 이해 할 수 있습니다.

2. 삽입 정렬 (Insertion Sort)

public class Main {

    public static void main(String[] args) {
        int[] arr = {8,5,6,2,4};
        insertion_sort(arr, arr.length);
        for(int i = 0; i < arr.length ; i ++) {
            System.out.println(arr[i]);
        }
    }
    private static void insertion_sort(int[] arr, int length) {
        for(int i = 1; i < length; i++) {
            int target = arr[i];
            int j = i - 1;
            while(j >= 0 && target < arr[j]) {
                arr[j + 1] = arr[j];	
                j--;
            }
            arr[j + 1] = target;
        }
    }
}

전체 코드는 위와 같이 됩니다. 아래의 코드에 대해서 좀 더 알아보겠습니다.

    private static void insertion_sort(int[] arr, int length) {
        for(int i = 1; i < length; i++) {
            int target = arr[i];
            int j = i - 1;
            while(j >= 0 && target < arr[j]) {
                arr[j + 1] = arr[j];	
                j--;
            }
            arr[j + 1] = target;
        }
    }

처음의 target 값의 index는 항상 전체 배열의 첫번째 index의 + 1로 시작합니다. 그러니까 +1 된 index의 target 값부터 이전의 값을 비교하겠다는 것 입니다.

index가 +1 된 target의 값이 이전 target 보다 작다면 이전 값의 배열의 위치를 한단계 밀어줍니다.

이후 밀면서 생긴 자리에 target 값을 넣어주면 됩니다.

            while(j >= 0 && target < arr[j]) {
                arr[j + 1] = arr[j];	
                j--;
            }

while 탈출 조건에 따라서 target이 arr[] 보다 큰 경우에 탈출하거나 0보다 작은경우 탈출하게 됩니다. &&이기 때문에 둘중 하나의 조건만 만족해도 반복문을 탈출해서 target값이 arr에 대입되게 됩니다.

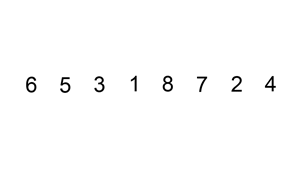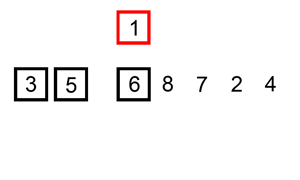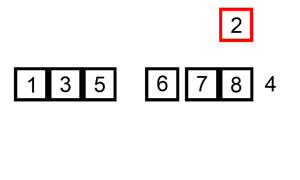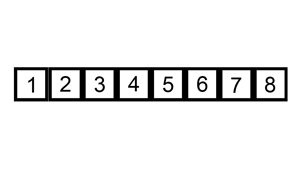
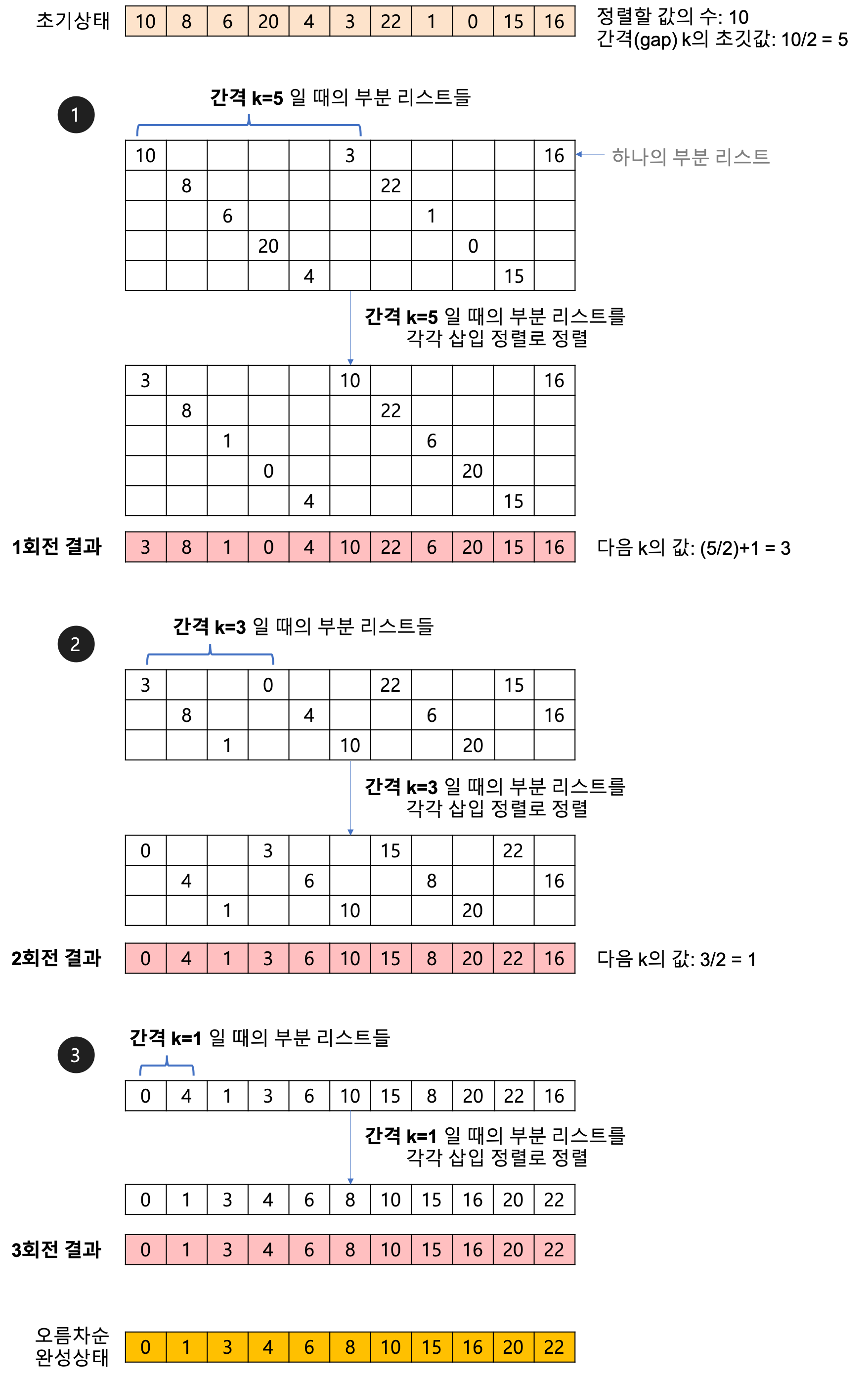
3. 쉘 정렬 (Shell Sort)

class Shell extends AbstractSort {
	public static void sort(Comparable[] a) {
		int N = a.length;
		int h = 1;
		while (h < N / 3)
			h = 3 * h + 1;
		while (h >= 1) {
			for (int i = h; i < N; i++)
				for (int j = i; j >= h && less(a[j], a[j - h]); j -= h)
					exch(a, j, j - h);
			h /= 3;
		}
	}
}

---

4. reference

https://gmlwjd9405.github.io/2018/05/06/algorithm-selection-sort.html
https://gmlwjd9405.github.io/2018/05/06/algorithm-insertion-sort.html
https://gmlwjd9405.github.io/2018/05/08/algorithm-shell-sort.html

https://en.wikipedia.org/wiki/Selection_sort
https://en.wikipedia.org/wiki/Insertion_sort