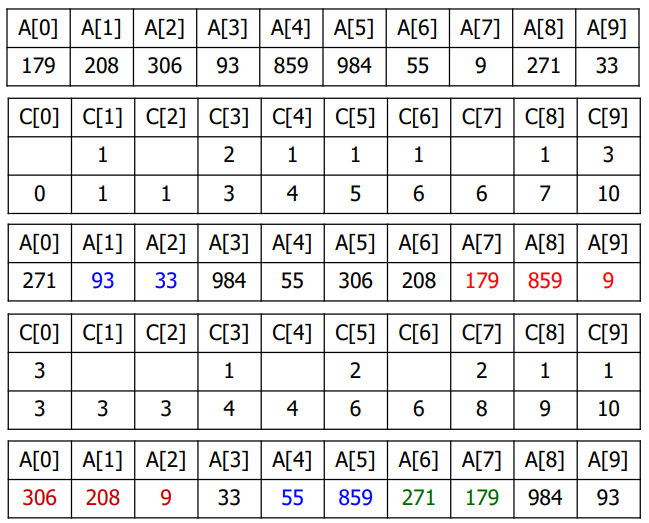
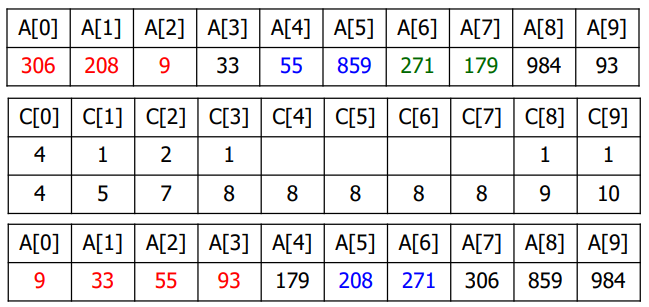
2. 선형 정렬 알고리즘
1. 계수 정렬 (Counting Sort)
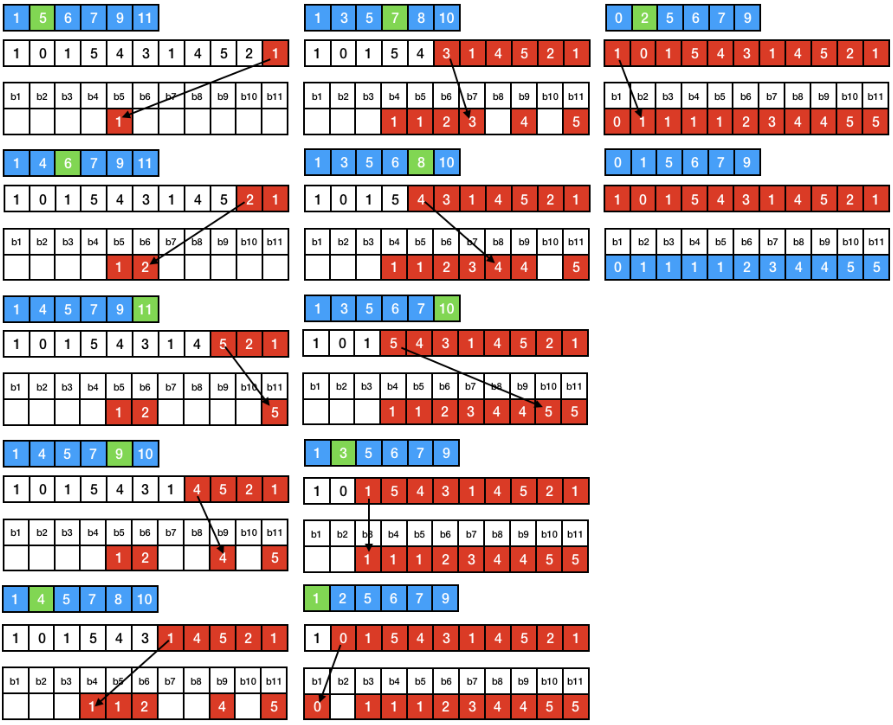
- 배열 Arr[11] = { 1, 0, 1, 5, 4, 3, 1, 4, 5, 2, 1 } 이 있다고 가정을 한다면 최대값이 5까지 있으므로 5까지의 Counting Array를 만들어줍니다. Counting Array는 Arr[] 배열의 원소의 갯수를 세어서 넣는 배열 입니다.
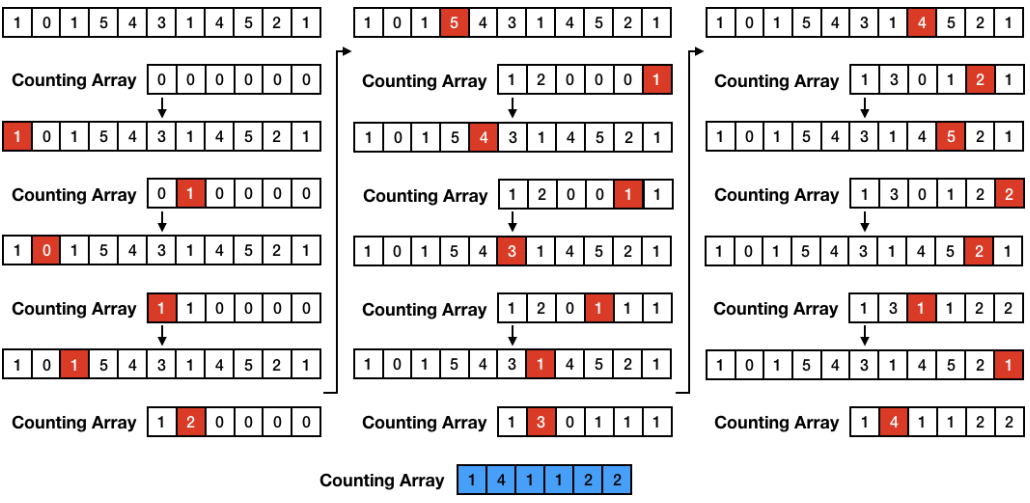
- Counting Array에 들어온 값을 이전 배열와 현재배열의 값을 더해서 다시 누적으로 배열 내부의 값이 커지게 다시 배열을 만들어 줍니다. 이 배열의 이름을 Counting Array' 라고 가칭으로 명명하겠습니다.

또다른 예시로 아래의 표로 설명하자면, 10까지 숫자가 있기 때문에 10까지 배열의 표로 만들어주고 존재하는 숫자만큼 +1씩 하여서 C 를 만들고 C' 그 C를 누적해서 만든 것을 알 수 있습니다.
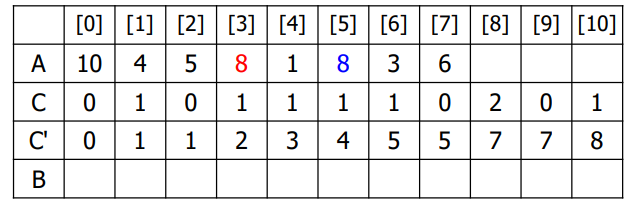
누적된 Counting Array를 해석해 보겠습니다.

2. 버킷 정렬 (Bucket Sort)
계수 정렬에서 여러 개의 구간을 하나의 버킷으로 통합
- 버킷의 크기 = 1일 경우 -> 계수 정렬
- 각 버킷을 정렬하는 별도 단계를 갖는다. (기수 정렬)
알고리즘의 동작 과정
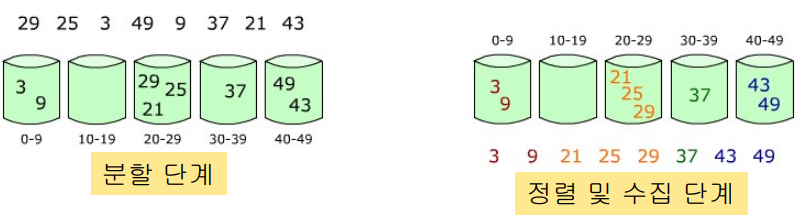
- 초기에 비어 있는 버킷을 준비
- 분할 단계: 입력 배열의 원소들을 해당되는 버킷에 저장
- 정렬 단계: 각 버킷을 정렬
- 수집 단계: 버킷을 차례로 방문하여 원소들을 원 배열에 저장
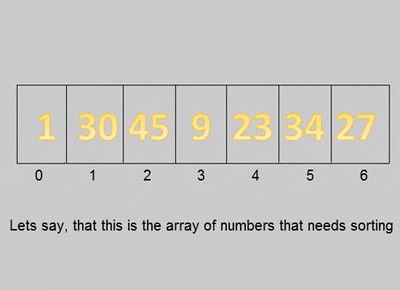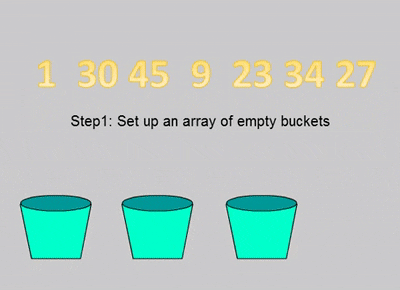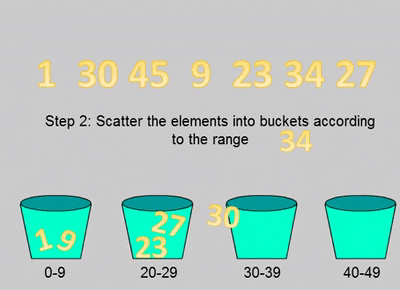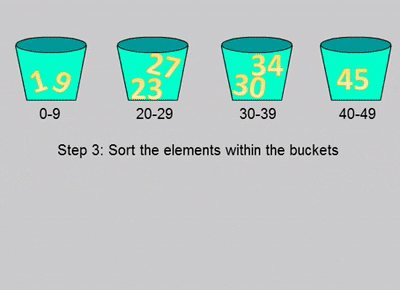
3. 기수 정렬 (Radix Sort)
1. 높은 자리 우선 정렬 (MSD sort)
K1 기준으로 버킷 정렬
각 버킷에 대해 K2 기준으로 다시 버킷 정렬예: 트럼프 카드
첫번째 단계: 무늬별로 4개의 버킷에 분할
두번째 단계: 각 버킷에서 숫자별로 다시 정렬
마지막 단계: 무늬 버킷을 순서대로 합친다
2. 낮은 자리 우선 정렬 (LSD sort)
K2 기준으로 버킷 정렬
각 버킷들을 합친다.
다시 K1 기준으로 버킷 정렬 (이때 stable sorting 알고리즘 사용)
버킷별로 별도 정렬 단계가 필요 없으므로 MSD보다 많이 사용
3. 예시 문제
LSD (radix sort) 를 이용한 기수 정렬 을 수행하여 배열에 저장된 데이터들을 오름차순으로 정렬하고자 한다 각 단계에서 정렬되는 순서를 나타내시오.

정렬 안된 원래 수: 427, 103, 054, 207, 009, 125
첫 번째 단계 정렬: 103, 054, 125, 427, 207, 009
두 번째 단계 정렬: 103, 207, 009, 125, 427, 054
세 번째 단계 정렬: 009, 054, 103, 125, 207, 427
4. LSD를 이용한 기수 정렬의 예
계수 정렬 (Counting Sort)를 이용하면 배열의 크기가 너무 극단적으로 커질 수가 있습니다. 그렇기 때문에 배열의 크기 손실을 막고자 기수 정렬를 사용하되 각 자리수를 계수 정렬로 정렬 시키는 경우 입니다.