정렬 알고리즘(4. 퀵정렬)

퀵 정렬

1. 개념

평균	최악	메모리	안정성
$O(N logN)$	$O(N^2)$	$O(1)$	X

Quick 정렬은 말 그대로 가장 빠른 정렬 방식입니다.
정렬을 하기 위해서는 모든 요소를 들여다봐야합니다(O(N)) 하지만 퀵 정렬 방식을 이용하면 $O(N logN)$ 의 시간복잡도로 정렬이 가능합니다. 흥미롭죠? 한번 살펴보시죠

퀵 정렬은 어떤 값을 기준으로 목록을 하위 목록으로 나눈 뒤 재귀를 반복하는 방식입니다. 하위 목록으로 계속해서 나누기때문에 $N logN$ 이 나오는 것이죠.

재귀의 과정은 말로 설명하기 어려우니 그림으로 살펴보겠습니다.

2. 동작 과정

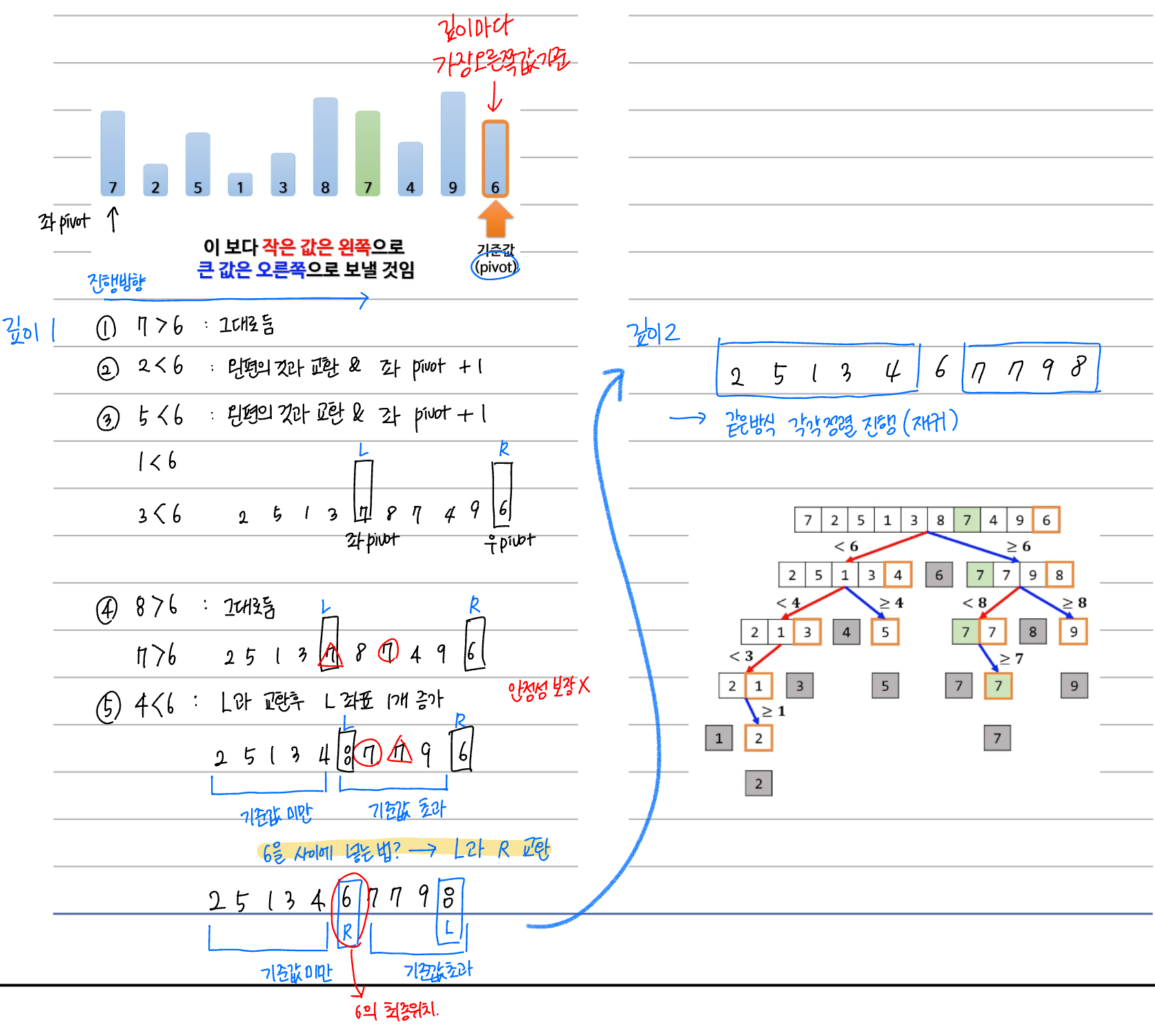
1회 순회 목표: 가장 오른쪽 값을 기준으로 기준값보다 작은 값들은 왼쪽에, 큰 값들은 오른쪽에 배치

1. 가장 왼쪽값-1(left)과 가장 오른쪽 값(right)을 기준으로 설정
2. left+1 요소부터 살펴보기 시작
   • 해당 요소가 기준값(right)보다 크면 그대로 유지
   • 해당 요소가 기준값(right)보다 작으면 left+1과 left 요소를 바꾸고 left 인덱스를 1 증가
3. 해당 과정을 right까지 계속해서 반복
4. 최종적으로 left 요소의 값과 right 요소의 값을 변경하면 순회 목표와 유사한 정렬이 완성

→ 해당 순회를 통해 기준 값의 위치는 선정이 되지만, 나머지 왼쪽과 오른쪽 값들은 정렬이 진행되지 않은 상태입니다.

그렇기 때문에 왼쪽과 오른쪽 각각 범위에 대해서도 위의 과정을 재귀로 넘겨주어 최종적으로 확정되는 요소들만 남게 됩니다.

3. 퀵 정렬의 시간 복잡도

퀵 정렬은 각 계층마다 N → 일정 부분 나뉜값 → 일정 부분 나뉜값을 방문하게 됩니다. 이를 쉽게 생각해 $O(N)$의 요소를 방문한다고 생각하겠습니다.

퀵 정렬은 재귀를 통해 반복되기때문에 재귀의 횟수가 시간 복잡도에 영향을 주게 됩니다. 평균적으로는 $\frac{1}{2}$씩 줄어든다고 가정하여 $O(longN)$으로 생각 할 수 있지만, 최악의 경우 1과 N-2 개씩 남게되는 상황이 있을 수 있기 때문에 $O(N)$까지 증가할 수 있습니다.

또, 재귀 함수를 활용하기 때문에 스택 메모리를 사용하게 되고 그 사용량은 $O(logN)$입니다.

이를 정리해보면 아래와 같습니다.

• 총 반복 횟수(재귀)
  • 매단계 좌우 균등 시: $O(longN)$
  • 매 단계 한쪽으로 몰릴 시: $O(N)$
• 각 계층마다 반복하는 요소 수: $O(N)$
• 시간 복잡도: 평균: $O(NlogN)$, 최악: $O(N^2)$
• 공간복잡도: $O(logN)$
• 안정성: ❌

구현

void quickSort(int[] arr, int left, int right) {
        if(left >= right) return;

        int pivotPos = partition(arr, left, right);

        quickSort(arr, left, pivotPos - 1);
        quickSort(arr, pivotPos + 1, right);
    }

    private int partition(int[] arr, int left, int right) {
        int pivot = arr[right];

        int i = left - 1;
        for(int j = left; j < right; j++){
            if(arr[j] < pivot){
                i++;
                swap(arr, i, j);
            }
        }

        int pivotPost = i + 1;
        swap(arr, pivotPost, right);

        return pivotPost;
    }

    public void swap(int[] arr, int i, int j) {
        int temp = arr[i];
        arr[i] = arr[j];
        arr[j] = temp;
    }

‼️주의
재귀를 호출하는 과정(quickSort)과 재귀 내에서 정렬하는 과정(partition)을 나누어서 구현하였습니다.

---

퀵 정렬은 실무에서 가장 많이 사용하는 알고리즘입니다. 직접 구현하기는 어려울지라도 그 개념만큼은 확실하게 익히세효!