정렬 알고리즘(5. 병합 정렬)

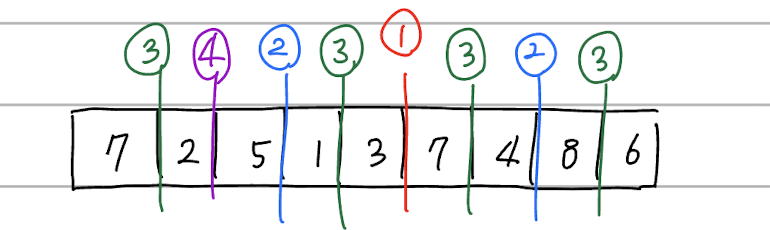
병합 정렬

1. 개념

평균	최악	메모리	안정성
$O(N logN)$	$O(N logN)$	$O(N)$	O

병합 정렬은 말 그대로 여러개였던 배열을 하나로 합치며 정렬하는 방식입니다.

기존에 정렬된 배열을 병합해 정렬된 배열의 완성본을 만드는 방식은 굉장히 쉽습니다. 병합 정렬에서는 이 방식을 그대로 사용합니다.
정렬을 하기 위해서는 기존의 배열을 여러개의 요소로 나눠야합니다.
하지만, 정렬되지 않은 배열을 어떻게 정렬된 여러개의 정렬된 배열로 나눌까요?

그 방법은 웃기게도 모두 1개의 요소로 이루어진 배열로 나누는 것입니다. 요소가 하나뿐이면 정렬이 된 상태로 볼 수 있기 때문이죠.

이후 나눠진 요소들을 정렬의 원칙을 지키며 하나씩 합치며 정렬하는 방식을 병합 정렬이라고 합니다.

2. 동작 과정

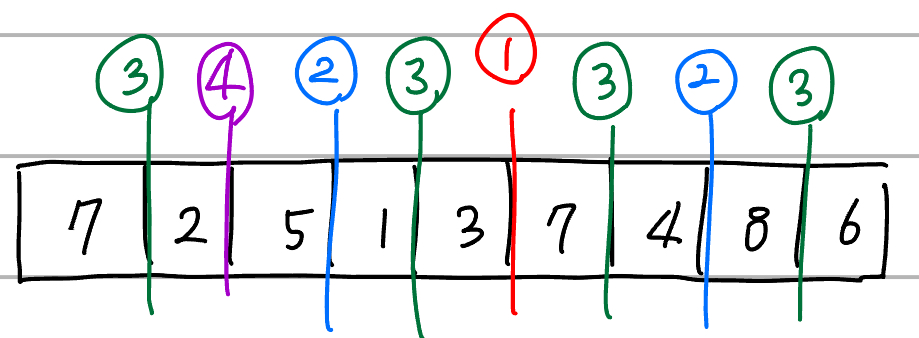
1. 주어진 배열을 정확하게 반씩 나눕니다.
2. 7,2,5,1,3,7,4,8,6 이렇게 총 8개의 배열이 남게 됩니다.
3. 나눈 방향의 역순으로 정렬된 상태로 배열을 합쳐나갑니다.

→ 최종적으로 정렬된 배열이 나옵니다.

3. 병합 정렬의 시간 복잡도

힙 정렬은 입력 배열을 힙 자료구조(완전이진트리)를 이용해 정렬하는 방식으로 배열 자체를 힙 구조로 정렬한 후 루트 노드를 반복적으로 삭제하며 정렬을 진행합니다.

힙 자료구조를 구성하는 것은 배열의 모든 원소를 한번씩 방문하여 제자리에서 힙의 속성을 만족하도록 재구성하는 것이기 때문에 $O(N)$의 시간복잡도가 필요하고

루트 노드를 삭제하며 남은 원소로 다시 힙을 구성하는 작업에서 힙의 높이만큼 시간이 소요되기 때문에 $O(logN)$이 소요되기 때문에 최종적으로 정렬을 위해서 $O(NlogN)$의 시간복잡도가 소요됩니다.

이를 정리해보면 아래와 같습니다.

• 힙 구성: $O(N)$
• 삭제 연산 & 힙 재구성: $O(logN)$
• 삭제 연산 횟수: $O(N)$
• 시간 복잡도: $O(N)$ + $O(NlogN)$ → $O(NlogN)$
• 공간복잡도: $O(N)$ → N개의 배열을 만들기 때문
• 안정성: O

---