[Programmers] 30. 인공지능 수학 기초 (3): 선형대수 (Linear Algebra) (3): 행렬연산과 선형조합

오류에 대한 지적이나 질문, 토의 환영합니다. 자유롭게 댓글 남겨주세요!.!

---

선형대수 (Linear Algebra) (3): 행렬연산과 선형조합

행렬 용어 정리

• 행렬 (Matrix)
  - 일반적으로 $n \times m$ 행렬

• 요소/원소 (Entry)

  • 행렬에 들어있는 수입니다.

• 행벡터 (Row Vector)

  • 하나의 행으로 이루어진 행렬을 의미합니다.

• 열벡터 (Column Vector)

  • 하나의 열로 이루어진 행렬을 의미합니다.
  • 일반적으로 선형대수에서 벡터라고 하면 열벡터를 의미합니다.

• 전치행렬 (Transpose Matrix)

  • 행렬의 행을 열로 열을 행으로 늘어놓은 행렬을 의미합니다.

• 영행렬 (Zero Matrix)

  • 행렬의 모든 요소가 0인 행렬을 의미합니다.
  • 행렬의 합에 대한 항등원 역할을 합니다.

• 정방행렬 (Square Matrix)

  • $n \times n$ 행렬을 말합니다.

• 주대각선/주대각원소 (Main Diagonal)

  • 정방 행렬의 행과 열의 숫자가 같은 위치에 있는 원소를 말한다. $a_{ii}$

• 항등행렬 (Identity Matrix)

  • 주대각선이 1이고 나머지 원소는 모두 0인 n차 정방행렬인 행렬을 말합니다.
  • 행렬의 곱에 대한 항등원 역할을 합니다.

• 내적 (inner product)

  • 벡터의 모든 요소들끼리 곱을 합친 결과를 말합니다.

행렬의 곱

• $A \times B = C$ 이고, $A = m \times r$ 행렬, $B = r \times n$행렬일 때,

• 행렬 $C = m \times n$행렬이 되고,

• 행렬 $C$의 각 요소 $C_{ij}$는 $A$의 $i-$번째 행벡터와 $B$의 $j-$번째 열벡터의 내적을 계산한 결과입니다.

• 행렬을 곱할 때 각 요소는 독립적이므로, 병렬처리(parallel processing)로 가속할 수 있습니다.

스칼라 / 벡터 / 행렬 / 텐서 계층적 구조 이해하기

• 스칼라 (Scalar)
  • 숫자 하나로 구성됩니다.
• 벡터 (Vector)
  • 여러 숫자가 일렬로 늘어선 구조입니다.
• 행렬 (Matrix)
  • 행과 열을 가지고 있는 구조입니다.
• 텐서 (Tensor)
  • 스칼라, 벡터 행렬을 아우르는 개념.
  • 숫자가 늘어설 수 있는 방향이 $k$개면 $k-$텐서라고 부릅니다.
• ex) $0-$텐서: 스칼라, $1-$텐서: 벡터, $2-$텐서: 행렬

---

분할행렬 (Partitioned Matrix) : 아주 중요

• 행렬의 구조가 복잡하여 이해하기 어려울 때,
  행렬을 추상적인 구조로 분할하면 행렬이나 행렬 연산을 파악하기 쉽습니다.

• 행렬을 조각(Partition) 단위로 분할하여 생각해도 무방합니다.

• 행렬은 부분행렬(Submatrix)로 이루어진 직사각형 구조로 확장해서 생각할 수 있습니다.

  

• 이런 행렬을 분할행렬(Partitioned Matrix) 혹은 블록행렬(Block Matrix)이라고 합니다.

• 행렬은 열벡터들의 모임이고 그렇게 본다면 행렬은 행벡터가 됩니다.

  

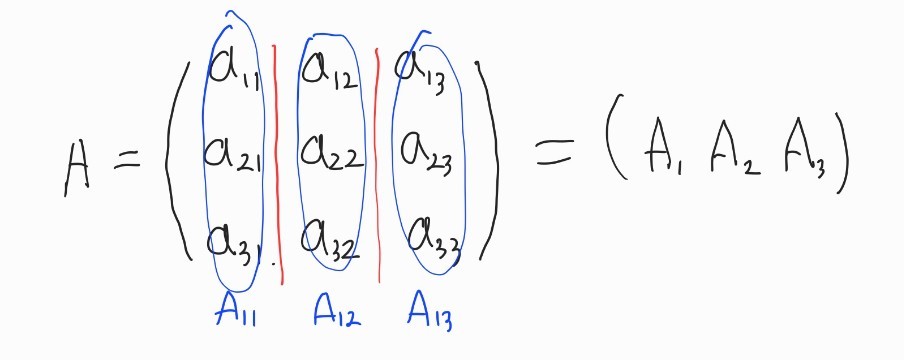
• 행렬은 행벡터들의 모임이고 그렇게 본다면 행렬은 열벡터가 됩니다.

  

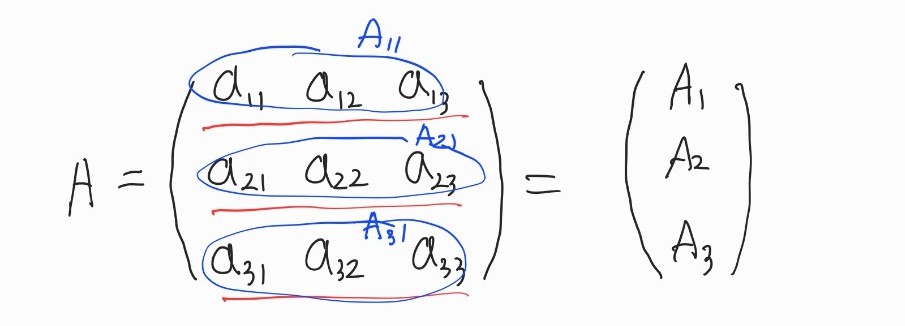
분할행렬로 행렬의 곱 이해하기

• 두 행렬의 곱 $A = m \times r$, $B = r \times n$일 때, $AB = C$를 수행합니다.
• 여기서, $B$ 행렬을 분할하여 열벡터의 모음으로 생각하면 다음과 같이 구조적으로 해석할 수 있습니다.
  (반대의 경우도 가능하다. A행렬을 분할하여 행벡터의 모음으로 생각하기)

  $AB = A\left[\begin{matrix}b_{1} ,\ \ b_{2}, \ ..., \ b_{n} \\\end{matrix}\right] = \left[\begin{matrix}Ab_{1} ,\ \ Ab_{2}, \ ..., \ Ab_{n} \\\end{matrix}\right] = C$

---

선형조합 (Linear Combination): 아주 중요

• 행렬 $A= m \times n$일 때,

• 행렬을 구조적으로 보면 행렬은 열벡터입니다.

  $A = \left[\begin{matrix}a_{11} ,\ \ a_{12}, \ ..., \ a_{1n} \\a_{21} ,\ \ a_{22}, \ ..., \ a_{2n} \\... \ \ \ \ \ ... \ \ \ \ ... \ \ \ \ ... \\a_{m1} ,\ \ a_{m2}, \ ..., \ a_{mn} \\\end{matrix}\right] = \left[\begin{matrix}a_{1} ,\ \ a_{2}, \ ..., \ a_{n} \\\end{matrix}\right]$

  • $m-$vector가 $n$개 있다고 볼 수 있습니다.
    다시 말해서, $m \times n$행렬은 $m-$벡터가 $n$개 있습니다.

• $Ax$는 행렬 A가 가지고 있는 열벡터의 선형조합이라고 볼 수 있습니다.

  $Ax = \left[\begin{matrix}a_{11} ,\ \ a_{12}, \ ..., \ a_{1n} \\a_{21} ,\ \ a_{22}, \ ..., \ a_{2n} \\... \ \ \ \ \ ... \ \ \ \ ... \ \ \ \ ... \\a_{m1} ,\ \ a_{m2}, \ ..., \ a_{mn} \\\end{matrix}\right]\left[\begin{matrix}x_{1} \\x_{2} \\ ... \\ x_{n} \\\end{matrix}\right] = \left[\begin{matrix}a_{1} ,\ \ a_{2}, \ ..., \ a_{n} \\\end{matrix}\right]\left[\begin{matrix}x_{1} \\x_{2} \\ ... \\ x_{n} \\\end{matrix}\right] = x_{1}a_{1} + x_{2}a_{2} + ... + x_{n}a_{n}$

  • 위와 같이 벡터 A와 x에 대한 가중치의 합으로 나타낼 수 있습니다.
  • 이를 선형조합이라고 합니다.
  • 다시말해, 벡터들에 대한 가중치의 합이라고 말하고 이것을 선형조합이라고 합니다.

정리

• 행렬 $A$의 열벡터를 가중치합으로 선형조합할 때,
• 벡터 $b$를 만들 수 있는 가중치 조합이 존재한다면,
• 선형시스템 $Ax = b$의 해는 존재합니다.
• 그 해는 가중치 $x_{i}$들로 구성된 $x$입니다.

결론

• 열공간 (Column space)
  행렬 $A$의 열벡터들에 대한 가능한 모든 선형조합의 결과를 모아 집합으로 구성할 수 있습니다.
  이 집합을 열공간이라고 하고 $col(A)$라고 표기합니다.

• 선형시스템 $Ax = b$가 해를 가지면, $b \in col(A)$

  Ex 1)
  $A = \left[\begin{matrix}-1 ,\ \ 3, \ 2 \\1 ,\ \ 2, \ -3 \\2 ,\ \ 1, \ -2 \\\end{matrix}\right]$

  • 행렬 $A$의 열벡터의 조합으로 $3-$벡터 $b$를 만들 수 있다면,
  • 선형시스템 $Ax = b$의 해는 존재한다.

• 선형시스템 $Ax = b$가 해가 없으면 $b \notin col(A)$

  Ex 2)
  $A = \left[\begin{matrix}-1 ,\ \ 3, \ 2 \\1 ,\ \ 2, \ -3 \\0 ,\ \ 0, \ 0 \\\end{matrix}\right]$

  • 행렬 $A$의 열벡터의 조합으로 만들 수 있는 공간은 $xy-$평면이다.
  • 벡터 $b$가 $xy-$평면에 존재하는 벡터라면, 선형시스템 $Ax = b$의 해는 존재한다.
  • 그러나, 벡터 $b$가 $xy-$평면에 벗어난 벡터라면 선형시스템 $Ax = b$의 해는 존재하지 않는다.

---

실습

스칼라, 벡터, 행렬, 그리고 텐서: 계층구조 이해하기

스칼라

import numpy as np

s = 3

print("a:", s)
print(np.shape(s))

a: 3
()

스칼라 -> 벡터

a = np.reshape(s, (1,))

print("a:", a)
print(np.shape(a))

a: [3]
(1,)

스칼라 -> 행렬

a = np.reshape(s, (1,1))

print("a:", a)
print(np.shape(a))

a: [[3]]
(1, 1)

스칼라 -> $3-$텐서

a = np.reshape(s, (1,1,1))

print("a:", a)
print(np.shape(a))

a: [[[3]]]
(1, 1, 1)

---

벡터

벡터: 24−벡터

a = np.array([1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23, 24])

print("a:", a)
print(np.shape(a))

a: [ 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24]
(24,)

벡터 -> 행렬

24-벡터 --> (1x24) 행렬

A = a.reshape(1,24)

print("A:", A)
print("A:", np.shape(A))

A: [[ 1  2  3  4  5  6  7  8  9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24]]
A: (1, 24)

24-벡터 --> (3x8) 행렬

A = a.reshape(3,8)

print("A:", A)
print("A:", np.shape(A))

A: [[ 1  2  3  4  5  6  7  8]
 [ 9 10 11 12 13 14 15 16]
 [17 18 19 20 21 22 23 24]]
A: (3, 8)

24-벡터 --> (6x4) 행렬

A = a.reshape(6,4)

print("A:", A)
print("A:", np.shape(A))

A: [[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]
 [13 14 15 16]
 [17 18 19 20]
 [21 22 23 24]]
A: (6, 4)

24-벡터 --> (24x1) 행렬

A = a.reshape(24,1)

print("A:", A)
print("A:", np.shape(A))

A: [[ 1]
 [ 2]
 [ 3]
 [ 4]
 [ 5]
 [ 6]
 [ 7]
 [ 8]
 [ 9]
 [10]
 [11]
 [12]
 [13]
 [14]
 [15]
 [16]
 [17]
 [18]
 [19]
 [20]
 [21]
 [22]
 [23]
 [24]]
A: (24, 1)

---

벡터 -> 3-텐서

24-벡터 --> (2x3x4) 텐서 (즉, 2개의 (3x4)행렬)

A = a.reshape(2, 3, 4)

print("A:", A)
print("A:", np.shape(A))

A: [[[ 1  2  3  4]
  [ 5  6  7  8]
  [ 9 10 11 12]]

 [[13 14 15 16]
  [17 18 19 20]
  [21 22 23 24]]]
A: (2, 3, 4)

벡터 -> 스칼라

## error: 벡터 a가 하나의 entry로 되어 있지 않기 때문에 아래의 경우는 모두 에러
# s = np.reshape(a, ())
# s = a.item() 

s = a[0]
print(s)

s = a.sum()
print(s)

1
300

---

행렬

A = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9,], [10, 11, 12]])

print(A)
print(np.shape(A))

[[ 1  2  3]
 [ 4  5  6]
 [ 7  8  9]
 [10 11 12]]
(4, 3)

---

행렬 -> 3-텐서

T = A.reshape(1, 4, 3)

print(T)
print(np.shape(T))

[[[ 1  2  3]
  [ 4  5  6]
  [ 7  8  9]
  [10 11 12]]]
(1, 4, 3)

T = A.reshape(2, 2, 3)

print(T)
print(np.shape(T))

[[[ 1  2  3]
  [ 4  5  6]]

 [[ 7  8  9]
  [10 11 12]]]
(2, 2, 3)

T = A.reshape(2, 3, 2)

print(T)
print(np.shape(T))

[[[ 1  2]
  [ 3  4]
  [ 5  6]]

 [[ 7  8]
  [ 9 10]
  [11 12]]]
(2, 3, 2)

---

행렬 -> 벡터

a = A.reshape(12,)

print(a)
print(np.shape(a))

[ 1  2  3  4  5  6  7  8  9 10 11 12]
(12,)

행렬 -> 스칼라

s = A[0,0]

print(s)
print(np.shape(s))

s = np.sum(A)

print(s)
print(np.shape(s))

1
()
78
()

---

텐서

T = np.array([[[1, 2, 3], [4, 5, 6]], [[7, 8, 9,], [10, 11, 12]]])

print(T)
print(np.shape(T))

[[[ 1  2  3]
  [ 4  5  6]]

 [[ 7  8  9]
  [10 11 12]]]
(2, 2, 3)

3-텐서 -> 행렬

A = T.reshape(4, 3)

print(A)
print(np.shape(A))

A = T.reshape(3, 4)

print(A)
print(np.shape(A))

[[ 1  2  3]
 [ 4  5  6]
 [ 7  8  9]
 [10 11 12]]
(4, 3)
[[ 1  2  3  4]
 [ 5  6  7  8]
 [ 9 10 11 12]]
(3, 4)

3-텐서 -> 벡터

a = T.reshape(12,)

print(a)
print(np.shape(a))

[ 1  2  3  4  5  6  7  8  9 10 11 12]
(12,)

3-텐서 -> 스칼라

s = T.sum()

print(s)
print(np.shape(s))

78
()

---

이 글은 프로그래머스 스쿨 인공지능 데브코스 과정에서 공부한 내용을 바탕으로 정리한 글입니다.