[Programmers] 31. 인공지능 수학 기초 (4): 선형대수 (Linear Algebra) (4): 좌표계 변환, 선형변환 기초

illstandtall·2021년 5월 1일

programmers python 선형대수 인공지능 수학

Programmers dev course

목록 보기

31/34

오류에 대한 지적이나 질문, 토의 환영합니다. 자유롭게 댓글 남겨주세요!.!

선형대수 (Linear Algebra) (4): 좌표계 변환, 선형변환 기초

좌표계 변환 (Change of Basis)

벡터의 표현: 고등 교과 과정 복습

벡터의 물리적 표현 (좌표계 없는)
- v의 크기: 화살표 길이
- v의 방향: 화살표의 방향
벡터의 수학적 표현 (좌표계 있는)
- 좌표계를 도입한 후 벡터의 시작점을 원점으로 맞추고 끝점의 위치를 벡터 v의 수학적 표현으로 정의헙니다.

좌표계 (coordinate system)

$I \times v = A \times v$
- 표준 좌표계( $I$ )에서 표현된 벡터 $v$
- 좌표계 $A$ 에서 표현된 벡터 $v$
$Ax = b$ 일 때,
- $A$ : 좌표계
- $x$ : 좌표값
- $b$ : 좌표값
좌표계를 행렬로 구성하고 벡터를 해당 좌표계에서의 좌표값이라고 말할 수 있습니다.

Ex) 1.
$2-$ 벡터 $v$ 가 표준좌표계에서 $(2, 3)$ 으로 표현되어 있습니다.
벡터 $(3, 1), (1, -2)$ 를 기저벡터로 가지는 새로운 좌표계를 도입했을 때,
해당 벡터는 $v$ 는 어떤 좌표값을 가질까요오? $(1, -1)$
=> $A = \left[\begin{matrix}3 \ \ \ 1\\ 1\ -2\end{matrix}\right]\left[\begin{matrix}x_{1}\\ x_{2}\end{matrix}\right] = \left[\begin{matrix}2\\ 3\end{matrix}\right]$

=> $x_{1}\left[\begin{matrix}3\\1\end{matrix}\right] + x_{2}\left[\begin{matrix}1\\-2\end{matrix}\right] =2\left[\begin{matrix}1\\0\end{matrix}\right] + 3\left[\begin{matrix}0\\1\end{matrix}\right]$
좌표계 A에서 표현된 좌표값 $(x_{1}, x_{2})$ 은 표준 좌표계 $\left[\begin{matrix}1 \ 0\\ 0\ 1\end{matrix}\right]$ 에서 좌표값 $(2, 3)$ 으로 표현할 수 있습니다.

다른 방법으로는 역행렬을 구하는 방법도 있습니다.
$\left[\begin{matrix}x_{1}\\ x_{2}\end{matrix}\right] = A^{-1}\left[\begin{matrix}2\\ 3\end{matrix}\right]$

Ex) 2
$3-$ 벡터 $v$ 가 표준좌표계에서 $(2, 1, 3)$ 으로 표현되어 있습니다.
벡터 $(1, 3, 1), (1, -2, -2)$ 를 기저벡터로 가지는 새로운 좌표계를 도입했을 때,
해당 벡터는 $v$ 는 어떤 좌표값을 가질까요오? $(1, 1)$
=> $A = \left[\begin{matrix}1 \ \ \ \ 1\\ 3\ -2 \\ 1\ -2\end{matrix}\right]\left[\begin{matrix}x_{1}\\ x_{2}\end{matrix}\right] = \left[\begin{matrix}2\\ 1 \\ 3\end{matrix}\right]$
=> $x_{1}\left[\begin{matrix}1\\3\\1\end{matrix}\right] + x_{2}\left[\begin{matrix}1\\-2\\-2\end{matrix}\right] =2\left[\begin{matrix}1\\0\\0\end{matrix}\right] + 1\left[\begin{matrix}0\\1\\0\end{matrix}\right] + 3\left[\begin{matrix}0\\0\\1\end{matrix}\right]$
좌표계 A에서 표현된 좌표값 $(x_{1}, x_{2})$ 느 표준 좌표계 $\left[\begin{matrix}1 \ 0 \ 0\\ 0\ 1 \ 0 \\ 0 \ 0 \ 1\end{matrix}\right]$ 에서 좌표값 $(2, 3, 1)$ 으로 표현할 수 있습니다.

선형변환 (Linear Transformation)

행렬은 선형함수입니다!
ex) 인공지능에서 합성곱, 역전파 등에 쓰입니다.

함수

함수는 맵핑 룰(mappeing rule)입니다.
정의역 (Domain): 입력이 정의되는 집합을 말합니다.
공역 (Codomain): 출력이 정의되는 집합을 말합니다.
치역 (range): 실제 함수의 출력이 나오는 부분집합을 말합니다.

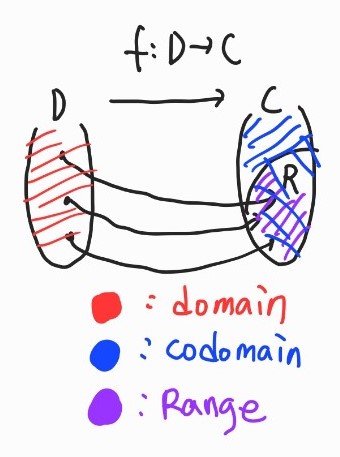
ex) $y = x^2 + 2x + 3$

domain/codomain: $R \rightarrow R$ or $f: R \rightarrow R$

programming:

float f(float x) { return x*x + 2*x + 3; }

domain: float x / codomain: float / range: x*x + 2*x + 3

선형함수

$f(x+y) = f(x) + f(y)$ ,
$f(cx) = cf(x)$
위 두 가지 조건을 만족하는 함수 $f$ 를 선형함수(linear function)라고 한다.

변환 (Transformation)

함수의 입력이 $n-$ 벡터이고, 출력이 $m-$ 벡터인 함수를 변환(transformation)이라고 한다.
특별히 입력과 출력이 같은 경우( $n=m$ ) 해당 변환을 연산자(operator)라고 한다.
예) mnist 손글씨 인식 문제 (비선형 변환)
$T: R^{28*28} \rightarrow R^{10}$

행렬변환 (Matrix Transformation)

$m \times n$ 행렬 $A$ 에 대해 $Ax$ 는 $n-$ 벡터를 입력으로 받아 $m-$ 벡터를 출력으로 내는 변환 $T_{A}(x) = A_{x}$ 로 볼 수 있습니다.
이 변환은 행렬이 정의하기 때문에 행렬변환이라고 합니다.

$T_{A}: R^n \rightarrow R^m$
그런데 행렬변환은 다음의 선형함수 성질을 모두 만족하기 때문에 선형변환입니다.
- $A(x+y) = A(x) + A(y)$ ,
- $A(cx) = cA(x)$
$A(x+y) = A(x) + A(y)$ 의
좌항 ' $+$ ' 는 $domain$ 에서 이루어진 $n-$ vector 끼리의 덧셈,
우항 ' $+$ '는 $codomain$ 에서 이루어진 $m-$ vector끼리의 덧셈입니다.
$A(cx) = cA(x)$ 의
좌항 스칼라 곱은 $domain$ 에서 이루어진 $n-$ vector 끼리의 곱,
우항 스칼라 곱은 $codomain$ 에서 이루어진 $m-$ vector끼리의 곱입니다.

정리

$m \times n$ 행렬은 $n-$ 벡터를 입력으로 받아 $m-$ 벡터를 출력으로 내는 선형변환이고,
임의의 선형변환은 행렬로 표현가능합니다.
즉, 행렬은 선형변환의 구현체입니다.

선형변환 코딩하기

행렬을 내가 원하는대로 디자인하는 것

구현하고자 하는 기능의 입력과 출력이 벡터로 정의되는지 확인합니다.
구현하고자 하는 기능이 선형인지 확인합니다.
입력이 n-벡터이고, 출력이 m-벡터이면 m*n 표준행렬을 구성합니다.

표준행렬 구하기

$n-$ 차원 표준기저벡터 { ${e_{1}, e_{2}, ..., e_{n}}$ }을 생각합니다.
각 $n-$ 차원 표준기저벡터 $e_{i}$ 에 대해,
우리가 원하는 기능을 동작시켜 얻은 결과인 $m-$ 차원 벡터 $T(e_{i})$ 를 표준행렬의 각 열에 적습니다.

예제1. 2차원 벡터를 입력으로 받아, 해당 벡터를 x-축에 프로젝션하는 기능 구현하기

생각 1. 이것이 변환인가?
=> 입력이 벡터이면 출력이 벡터여야 합니다.. Yes! $(3, 2) \rightarrow (3, 0)$

생각 2. 선형변환인가??? 선형 함수인가?
=> 입력이 직선벡터이고, 출력도 직선벡터여야 합니다.. Yes!

생각 3. 선형변환을 행렬로 표현할 수 있다!
=> 입력이 2차원 출력이 2차원인 $2 \times 2$ 행렬을 구성할 것입니다.

생각 4. 열벡터를 두 번 채우면 되겠군.

생각 5. 첫번째 열을 채우면 됩니다.
입력으로 첫 번째 기저벡터 $(1, 0)$ 를 넣었을 때 내가 원하는 기능을 돌려보면 $(1, 0)$ 이 됩니다.
=> $\left[\begin{matrix}1 \ *\\ 0\ *\end{matrix}\right]$

생각 6. 두번째 열을 채웁니다.
입력으로 두 번째 기저벡터 $(0, 1)$ 을 넣었을 때 내가 원하는 기능을 돌려보면 $(0, 0)$ 이 됩니다.
=> $\left[\begin{matrix}1 \ 0\\ 0\ 0\end{matrix}\right]$

생각 7. 함수를 모두 짰습니다. 선형변환 코딩이 모두 끝났습니다.
=> $\left[\begin{matrix}1 \ 0\\ 0\ 0\end{matrix}\right]\left[\begin{matrix}x \\ y\end{matrix}\right] = \left[\begin{matrix}x \\ 0\end{matrix}\right]$

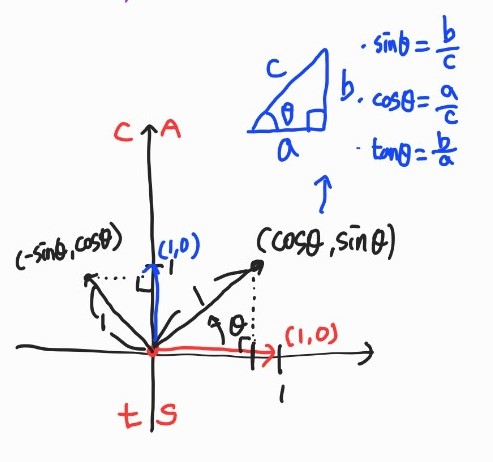
예제 2. 2차원 벡터를 입력으로 받아, 해당 벡터를 반시계방향으로 $\theta$ 만큼 회전하는 기능을 구현하기

생각 1. 이것이 변환인가?
=> Yes! 벡터를 입력으로 넣으면 출력으로 회전된 벡터가 나옵니다.

생각 2. 선형변환인가?
=> Yes 직선을 입력으로 넣었을때 회전된 직선이 나옵니다.

생각 3. 입력으로 2차원 벡터, 출력으로 2차원 벡터 $2 \times 2$ 행렬을 구성하면 됩니다.

생각 4. 열벡터를 채웁니다.
첫 번째 열벡터를 채울 때 $domain$ 에서 기저벡터 $(1, 0)$ [x축]을 넣고 원하는 기능을 생각해보면 $(cos\theta, sin\theta)$ 가 나옵니다.
=> $\left[\begin{matrix}cos\theta \ *\\ sin\theta\ *\end{matrix}\right]$

생각 5. 두번째 열 벡터를 채웁니다.
기저벡터 $(0, 1)$ [y축]을 넣고 원하는 기능을 생각해보면 $(cos(\theta+90), sin(\theta+90)) = (-sin\theta, cos\theta)$
=> $\left[\begin{matrix}cos\theta \ -sin\theta\\ sin\theta\ \ \ \ cos\theta\end{matrix}\right]$

생각 6. 함수를 모두 짰습니다.
=> $\left[\begin{matrix}cos\theta \ -sin\theta\\ sin\theta\ \ \ \ cos\theta\end{matrix}\right]\left[\begin{matrix}x \\ y\end{matrix}\right] = \left[\begin{matrix}xcos\theta - ysin\theta \\ xsin\theta + ysin\theta\end{matrix}\right]$

참고