[Programmers] 33. 인공지능 수학 기초 (6): 선형대수 (Linear Algebra) (6): SVD, PCA, 최소제곱법

SVD, PCA, 최소제곱법

행렬분해 (3): 특이값 분해: SVD

• 특이값 분해 (SVD: singular value decomposition): 중요

• LU, QR 분해는 $n \times n$ 정방행렬에서만 사용이 가능합니다.

• 특이값 분해는 일반적인 $m \times n$ 행렬에 관한 행렬분해입니다.

• SVD는 직교분할, 확대축소, 차원변환 등과 관련이 있습니다.

• $A = UDV$

  • $U$: $m \times m$인 $m$차원 회전행렬 - 정규직교행렬(열벡터)
  • $D$: $m \times n$인 $n$차원 확대/축소 - 확대/축소 크기에 따른 정렬형태 대각행렬 - 축방향으로 확대/축소
  • $V^T$: $n \times n$인 n차원 회전행렬 - 정규직교행렬(행벡터)

• SVD의 의미

  • $U$: 입력 차원인 $R^m$공간에서의 회전
  • $D$: 입력 차원인 $R^n$ 공간에 대해 축방향으로의 확대축소한 후, $R^n \rightarrow R^m$으로차원변환
  • $V$: 입력차원인 $R^n$ 공간에서의 회전

• SVD의 활용
  - $A$의 특이값 분해 $U, D, V$는 각각 열벡터의 순서대로
  행렬 $A$의 열벡터가 어떤 방향으로 강한 응집성을 보이고 있는지를 분석한 것입니다.
  - 열벡터를 순서대로 $p$개 취한다면,
  강한 응집성을 가지는 $p$개의 방향으로 수선의 발을 내린 $A$의 근사치 $A'$를 재구성 할 수 있습니다.
  - 영상처리 등에서 많이 쓰입니다.

  예
  $\ \ \ \ \ \ \ A_{3 \times 2} \ \ \ \ \ \ = \ \ \ \ \ \ \ \ \ U_{3 \times 3} \ \ \ \ \ \ \ \ \ \ \ \ \ \ D_{3 \times 2} \ \ \ \ \ \ \ \ \ \ {V^T}_{2 \times 2}$
  $\left[\begin{matrix}2 \ \ \ 2 \\ -\frac{1}{2}\ \ \ \ \frac{1}{2} \\ -2 \ -2\end{matrix}\right] = \left[\begin{matrix}\frac{1}{\sqrt{2}} \ \ \ 0 \ \ \ \frac{1}{\sqrt{2}} \\ 0 \ \ \ \ 1 \ \ \ \ 0 \\ -\frac{1}{\sqrt{2}} \ 0 \ -\frac{1}{\sqrt{2}}\end{matrix}\right] \ \ \ \left[\begin{matrix}4 \ \ \ \ \ \\ \ \ \ \ \ \frac{1}{\sqrt{2}} \\ \ \ \ \ \ \ \ \end{matrix}\right] \ \ \left[\begin{matrix}\frac{1}{\sqrt{2}} \ \ \ \frac{1}{\sqrt{2}} \\ -\frac{1}{\sqrt{2}}\ \ \ \ \frac{1}{\sqrt{2}}\end{matrix}\right]$
  $\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = \ \ \ \ \ \ \ \ \ {U^{'}}_{3 \times 1} \ \ \ \ \ \ \ \ \ \ \ \ \ \ {D^{'}}_{1 \times 1} \ \ \ \ \ \ \ \ \ \ {{V^{'}}^T}_{1 \times 2} \ \ \ \ \ \ \ = \ \ \ \ {A^{'}}_{3 \times 2}$
  $\ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ \ = \ \ \ \ \ \ \ \ \left[\begin{matrix}\frac{1}{\sqrt{2}}\\ 0\\ -\frac{1}{\sqrt{2}}\end{matrix}\right] \ \ \ \ \ \ \ \ \ \ \ \left[\begin{matrix}4\end{matrix}\right] \ \ \ \ \ \ \ \ \ \ \ \ \ \left[\begin{matrix}\frac{1}{\sqrt{2}} \ \ \ \frac{1}{\sqrt{2}}\end{matrix}\right] \ \ \ \ = \left[\begin{matrix}2 \ \ \ 2 \\ 0\ \ \ 0 \\ -2 \ -2\end{matrix}\right]$
  $A' = \left[\begin{matrix}2 \ \ \ 2 \\ 0\ \ \ 0 \\ -2 \ -2\end{matrix}\right]$ => 응집성이 낮은 것을 버린 결과 => 유의미한 부분을 더 돋보이게 할 수 있습니다.

---

주성분 분석: (PCA: principal component analysis)

• 다수의 $n$차원 데이터에 대해 데이터의 중심으로부터 데이터의 응집력이 좋은 $n$개의 직교방향을 분석하는 방법입니다.

• 데이터의 공분산행렬(covariance matrix)에 대한 고유값(eigenvalue) 분해에 기반을 둔 직교분해입니다.

1. 데이터의 중심 구하기 -> 데이터의 평균 $m$

   • $m = \frac{1}{k}\sum_{i=1}^K x_{i}$

2. 가진 임의의 데이터 $x_{i}$와 중심간의 벡터의 외적을 통해 차원을 쌓습니다.

   • $C = \frac{1}{k}\sum_{i=1}^K (x_{i}-m)(x_{i}-m)^T$

• $C = W D W^t$
  • $W$: $n$차원 회전행렬 - 정규 직교행렬
  • $D$: $n$차원 확대축소 - 대각행렬 고유값이 크면 응집성이 큽니다.

PCA의 활용: 벡터공간의 최소제곱법

집합과 공간

• 집합(Set)
  임의의 원소(element)를 수집하여 만든 모임을 말합니다.

• 연산에 닫혀있다
  집합에 속해있는 원소를 뽑아 연산을 실행항 결과가 다시 그 집합에 속한 경우를 말합니다.

• 공간(Space): 다음 두 연산에 닫혀있는 집합을 말합니다.
  1. 덧셈 연산에 닫혀있다.
  2. 스칼라 곱 연산에 닫혀있다.

• 열공간 (column space)

  • 행렬 $A$의 열벡터들에 대한 가능한 모든 선형조합의 결과를 모아 집합으로 구성한 공간을 말합니다.
  • 해가 있다 : 열공간 내에 있다는 것을 말합니다.
  • 해가 없다: 열공간을 벗어난다는 것을 말합니다.

최소제곱법 (least squares method)

• 선형시스템 $Ax = b$에 대한 해가 없음에도 불구하고, 가장 가까운 해답(근사해)을 내는 방법입니다.

• 벡터 $b$를 행렬 $A$가 정의하는 열공간으로 투영한 결과를 가장 가까운 답인 $x$로 봅니다.

• $A\overline{x} = \overline{b} = proj_{a}b$

• 목표 $b$와 달성가능한 목표 $\overline{b}$의 차이를 나타내는 벡터 $(b-\overline{b})^2$의 길이를
  최소화 시키는 의미를 지니기 때문에 최소제곱법이라고 불립니다.

$Ax = b$
=> $A^TA\overline{x} = A^Tb$
=> $\overline{x} = (A^TA)^{-1}A^Tb$

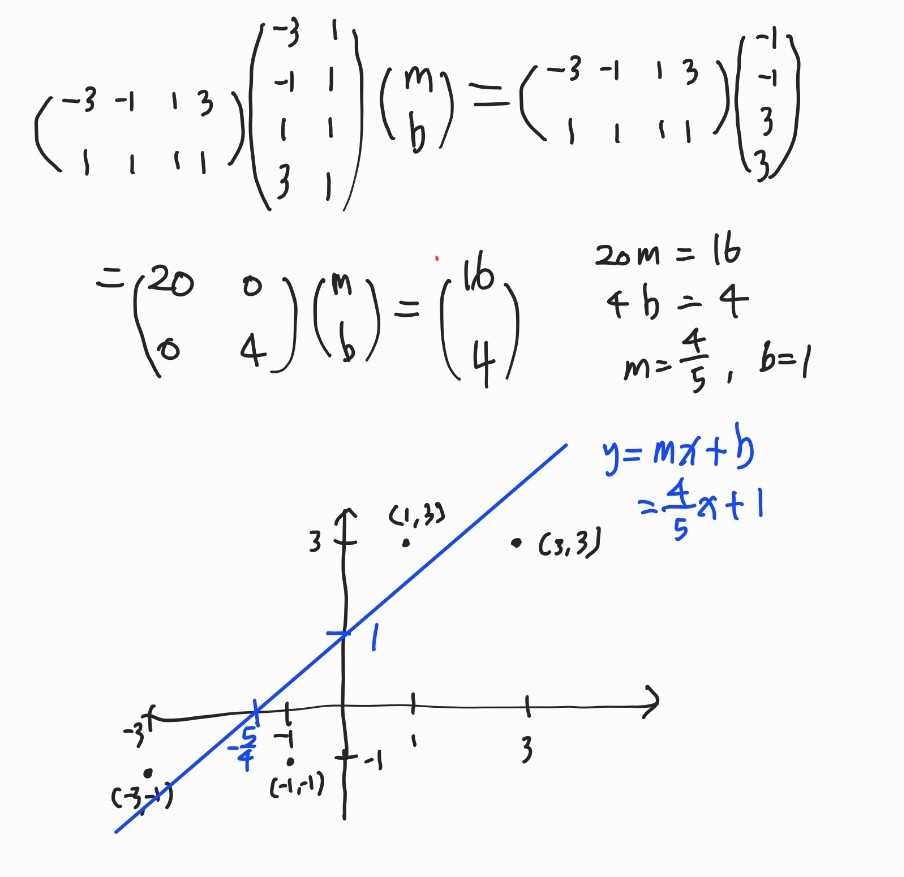
최소제곱법의 응용: 선형회기 (linear regression)

1. 선형시스템 구성 $Ax = b$
   $\left[\begin{matrix}-3 \ 1 \\ -1\ 1 \\ 1 \ 1 \\ 3 \ 1\end{matrix}\right]\left[\begin{matrix}m \\ b\end{matrix}\right] = \left[\begin{matrix}-1 \\ -1 \\ 3 \\ 3 \end{matrix}\right]$
   => $A_{4 \times 2} \overline{x}_{2 \times 1} = b_{4 \times 1}$
2. 최소제곱법 적용
   $(A^TAx)_{2 \times 2}\overline{x}_{2 \times 1} = (A^Tb)_{2 \times 1}$
3. 

---

SVD, PCA, 최소제곱법 실습해보기

SVD

import numpy as np

A = np.array([[1, 1], [-2, 2], [-1, -1]])

print("A:")
print(A)

A:
[[ 1  1]
 [-2  2]
 [-1 -1]]

U: 정규직교행렬(열벡터), UU: 열벡터를 한 개 취함

U = np.array([[1/1.414, 0, 1/1.414], [0, 1, 0], [-1/1.414, 0, 1/1.414]])

UU = U[:,:1]

print("U:")
print(U)
print("UU:")
print(UU)

U:
[[ 0.70721358  0.          0.70721358]
 [ 0.          1.          0.        ]
 [-0.70721358  0.          0.70721358]]
UU:
[[ 0.70721358]
 [ 0.        ]
 [-0.70721358]]

D: 확대/축소 행렬, DD: 강한 응집성 보이는 열

D = np.array([[4, 0], [0, 1/1.414], [0, 0]])

DD = D[:1,:1]

print("D")
print(D)

print("DD")
print(DD)

D
[[4.         0.        ]
 [0.         0.70721358]
 [0.         0.        ]]
DD
[[4.]]

Vt: 정규직교행렬(행벡터)), VVt: 행벡터 한 개를 취함

Vt = np.array([[1/1.414, 1/1.414], [-1/1.414, 1/1.414]])

VVt = Vt[:1,:]

print("Vt")
print(Vt)

print("VVt")
print(VVt)

Vt
[[ 0.70721358  0.70721358]
 [-0.70721358  0.70721358]]
VVt
[[0.70721358 0.70721358]]

AA:

AA = U @ D @ Vt

print("AA")
print(AA)

AA
[[ 2.00060418  2.00060418]
 [-0.50015105  0.50015105]
 [-2.00060418 -2.00060418]]

강한 응집성

UU @ DD @ VVt

array([[ 2.00060418,  2.00060418],
       [ 0.        ,  0.        ],
       [-2.00060418, -2.00060418]])

---

PCA

import numpy as np
from sklearn.decomposition import PCA

X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
pca = PCA(n_components=2)
pca.fit(X)

PCA(n_components=2)

---

print(pca.explained_variance_ratio_)

[0.99244289 0.00755711]

---

print(pca.singular_values_)

[6.30061232 0.54980396]

---

print(pca.components_)

[[-0.83849224 -0.54491354]
 [ 0.54491354 -0.83849224]]

---

최소제곱법

import numpy as np

A = np.array([[-3, 1], [-1, 1], [1, 1], [3, 1]])
b = np.array([-1, -1, 3, 3])
print('A:', A)
print('b:', b)

A: [[-3  1]
 [-1  1]
 [ 1  1]
 [ 3  1]]
b: [-1 -1  3  3]

At = A.transpose()
print(At)

[[-3 -1  1  3]
 [ 1  1  1  1]]

• 전치행렬 곱

AtA = At @ A
print(AtA)

Atb = At @ b
print(Atb)

AtA_inv = np.linalg.inv(AtA)
print(AtA_inv)

[[20  0]
 [ 0  4]]
[16  4]
[[0.05 0.  ]
 [0.   0.25]]

• $m=0.8, b=1$

xx = AtA_inv @ Atb
print(xx)

[0.8 1. ]

• $b$에서 최소제곱법으로 구한 직선에 수선의 발을 내려 $\overline{b}$를 구했다.!

bb = A @ xx
print(bb)

[-1.4  0.2  1.8  3.4]

---

이 글은 프로그래머스 스쿨 인공지능 데브코스 과정에서 공부한 내용을 바탕으로 정리한 글입니다.