[Programmers] 32. 인공지능 수학 기초 (5): 선형대수 (Linear Algebra) (5): 벡터의 투영/사영, 직교 행렬, QR 분해
Programmers dev course

오류에 대한 지적이나 질문, 토의 환영합니다. 자유롭게 댓글 남겨주세요!.!
벡터의 투영/사영, 직교 행렬, QR 분해
벡터의 내적 (Inner Product)
-
벡터는 크기와 방향을 가진 물리량을 말합니다.
-
좌표계 없이:
-
좌표계 에서:
-
두 벡터의 내적이 0이면 두 벡터는 직교(Orthogonal: )합니다.
- 물리적 의미:
와 가 직교일 때, 방향으로의 전진은 방향에서 전혀 측정되지 않는다는 의미를 가집니다.
- 물리적 의미:
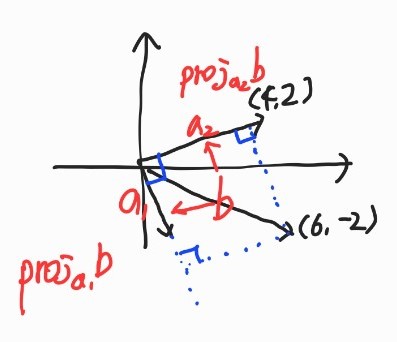
벡터의 투영/사영(Projrction)
- 벡터 를 벡터 위에 투영한 결과:
=> : 크기(기저 에 대한 좌표값), : 방향 - 벡터 를 벡터 위에 투영하고 남은 보완벡터(complement vector):
- 투영과 보완벡터는 서로 직교이다.
직교 행렬 (orthogonal matrix)
-
직교 좌표계에 대한 행렬 표현입니다.
-
직교 행렬 (orthogonal matrix)
- 주어진 행렬의 모든 열벡터가 서로 직교하는 경우입니다.
- 직교행렬은 직교 좌표계를 의미합니다.
-
-
정규 직교 행렬 (orthonormal matrix)
- 주어진 행렬이 직교 행렬이고 모든 열벡터의 크기가 1인 행렬을 말합니다.
- 회전행렬이라고도 합니다.
-
직교 행렬을 이용한 선형시스템
-
선형시스템 에서 행렬 가 직교행렬이면, 해 는 역행렬의 계산 없이 구할 수 있습니다.
-
의 번째 요소는 투영으로 계산할 수 있습니다.
즉, 벡터 를 행렬 의 각 열벡터 에 투영한 연산 로 부터 알 수 있습니다. -
의 번째 요소와 번째 요소의 계산은 독립적이므로 의 계산을 병렬로 처리할 수 있습니다.
예제)
<=>- =
- =
정규직교행렬을 이용한 선형시스템
-
선형시스템 에서 행렬 가 정규직교행렬이면, 해 는 역행렬의 계산 없이 구할 수 있습니다.
-
의 번째 요소는 내적으로 계산할 수 있습니다.
즉, 벡터 를 행렬 의 각 열벡터 에 투영한 연산 로 부터 임을 계산할 수 있습니다. -
의 번째 요소와 번째 요소의 계산은 독립적이므로 의 계산을 병렬로 처리할 수 있습니다.
예제)
<=>- =
- =
행렬분해 (2): QR 분해 (QR Decomposition)
-
그람슈미트 과정을 행렬로 코드화한 것입니다.
-
주어진 행렬에서 정규직교행렬을 추출하는 행렬 분해입니다.
-
행렬 를 의 꼴로 변형시키는 분해입니다.
- = (Orthonormal matrix) (Upper triangular matrix)
-
QR 분해의 장점
<=>
=> => : 내적으로 쉽게 계산 가능
=> => : 후방 대치법으로 쉽게 계산 가능
- QR 분해의 활용
- 를 이용한 부분에서 병렬처리로 빨리계산할 수 있습니다. (은 불가능)
- 가 자주 업데이트되는 경우 사용합니다.
행렬분해: LU 분해 vs QR 분해
- LU 분해: 선형시스템을 풀 때 병렬처리할 수 없습니다.
- QR 분해: Q행렬이 꽉찬 구조이므로 메모리를 더 많이 차지합니다.

이 글은 프로그래머스 스쿨 인공지능 데브코스 과정에서 공부한 내용을 바탕으로 정리한 글입니다.
