Leetcode 222. Count Complete Tree Nodes with Python - 리뷰 O

문제

Given the root of a complete binary tree, return the number of the nodes in the tree.

According to Wikipedia, every level, except possibly the last, is completely filled in a 
complete binary tree, 
and all nodes in the last level are as far left as possible. 
It can have between 1 and 2h nodes inclusive at the last level h.

Design an algorithm that runs in less than O(n) time complexity.

완전 이진 트리 root가 주어졌을때, O(n)의 시간복잡도 안에 노드의 갯수를 구하시오.

예시

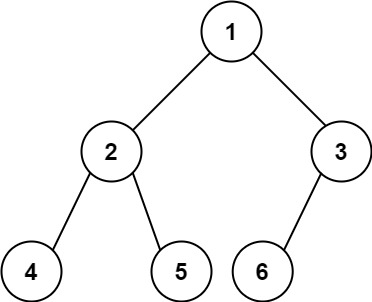
Input: root = [1,2,3,4,5,6]
Output: 6

제한

• 트리 내부 값의 범위 [0, 5 * 10^4].
• 0 <= Node.val <= 5 * 10^4
• 반드시 완전트리가 주어진다.

풀이법

첫번째로 내가 생각해낸 방법은 단순 재귀를 이용한 방법이다.

생각보다 속도가 빠르게 나와 당황했다.

엄청 느릴줄 알았는데

def count(root: Optional[TreeNode]):
    if root == None: return 0;
    return count(root.left) + count(root.right) + 1

class Solution:
    def countNodes(self, root: Optional[TreeNode]) -> int:
        return count(root)

근데 이 방식은 완전트리인걸 이용하지 않지 않나 싶어서

이게 완벽하게 채워진 트리일때를 따로 빼서 O(1)에 계산할수 있게 했다.

왼쪽 노드 끝까지 갔을때 길이와 오른쪽 노드 끝까지 갔을때 길이가 같으면 2^길이 - 1 을 리턴하도록 했다.

def count(root: Optional[TreeNode]):
    if root == None: return 0;
    return count(root.left) + count(root.right) + 1

class Solution:
    def countNodes(self, root: Optional[TreeNode]) -> int:
        left = 0
        right = 0
        rl = rr = root

        while rl != None:
            rl = rl.left
            left += 1
        while rr != None:
            rr = rr.right
            right += 1

        return count(root) if left != right else 2 ** (left) - 1
        

99.14%! 아주 만족스러운 결과가 나왔다.

( 2024 / 12 / 10 )

복기

• 에 왜 저게 O(1)이라고 자랑스럽게 써놨지 ㅋㅋㅋ 노드 갯수 N이면 O(LogN) 아닌감? ㅋㅋㅋ

class Solution:
    def countNodes(self, root: Optional[TreeNode]) -> int:
        if not root:
            return 0

        return self.countNodes(root.left) + self.countNodes(root.right) + 1

• 세상은 간단한게 최고다 깔끔하게 짜자잇