Leetcode 98. Validate Binary Search Tree with Python - 리뷰 O

문제

Given the root of a binary tree, determine if it is a valid binary search tree (BST).

A valid BST is defined as follows:

- The left subtree of a node contains only nodes with keys less than the node's key.
- The right subtree of a node contains only nodes with keys greater than the node's key.
- Both the left and right subtrees must also be binary search trees.

예시

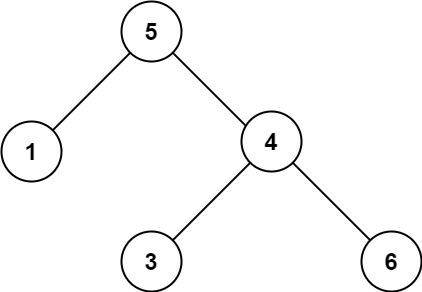
Input: root = [5,1,4,null,null,3,6]
Output: false
Explanation: 루트 Node의 값 [ 5 ] 보다 오른쪽 노드의 값 [ 4 ] 가 작다.

제한

• 트리 내 노드 갯수 범위 [1, 104].
• 2^31 <= Node.val <= 2^31 - 1

풀이법

자칫 잘못하면 Node의 왼쪽값과 오른쪽 값만 검사하면 된다고 생각할수도 있으니 이는 오산이다.

Binary search tree의 경우 Node의 왼쪽 Subtree의 모든 값 이 노드 값보다 작아야 하고

Node의 오른쪽 Subtree의 모든 값 이 노드 값보다 커야 하기 때문이다.

즉 크기 범위가 전체 Subtree에 적용되어야 하기에 재귀 패러미터에 각각 lowerBound와 upperBound를 추가해야 한다.

def validity(root: Optional[TreeNode], lowerBound: int, upperBound: int):
    if root == None: return True
    if root.val <= lowerBound or root.val >= upperBound: return False
    return validity(root.left, lowerBound, root.val) and validity(root.right, root.val, upperBound)

class Solution:
    def isValidBST(self, root: Optional[TreeNode]) -> bool:
        return validity(root, -(2**32-1), 2**32)

( 2024 / 12 / 10 )

복기

class Solution:
    def isValidBST(self, root: Optional[TreeNode], lower: int = -float('inf'), upper: int = float('inf')) -> bool:
        if root is None:
            return True

        if root.val <= lower or root.val >= upper:
            return False

        return self.isValidBST(root.left, lower, root.val) and self.isValidBST(root.right, root.val, upper)

따로 헬퍼 함수를 만들지 않고 해봤다.
옵셔널 패러미터를 임의로 추가해도 되네, 따로 검사는 안하는듯