Leetcode 2290. Minimum Obstacle Removal to Reach Corner

문제

You are given a 0-indexed 2D integer array grid of size m x n. Each cell has one of two values:

0 represents an empty cell,
1 represents an obstacle that may be removed.
You can move up, down, left, or right from and to an empty cell.

Return the minimum number of obstacles to remove so you can move from the upper left corner (0, 0) to the lower right corner (m - 1, n - 1).

• 그리드에 0은 장애물이 없는것, 1은 장애물이 있는것이다.
• (0, 0) 에서 그리드의 오른쪽 맨 아래까지 이동할때 최소한으로 거칠수 있는 장애물의 수를 구하라

예시

• 0
  • 장애물을 하나도 거치지 않고도 갈수 있다.

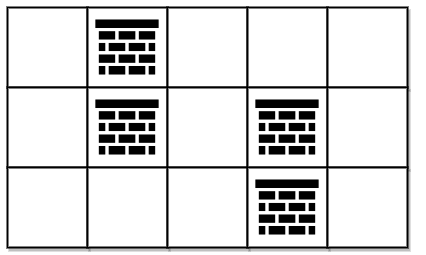
제한

• $m == grid.length$
• $n == grid[i].length$
• $1 <= m, n <= 10^5$
• $2 <= m * n <= 10^5$
• 그리드는 0 혹은 1로만 구성된다.
• $grid[0][0] == grid[m - 1][n - 1] == 0$

풀이

• BFS와 최소힙을 이용한다.
• 최소힙을 이용해 지우는 수가 제일 적은것을 우선하여 계속 탐색해 나간다.
• 지우는 수가 적을때만 추가하고, 그렇지 않을 경우는 제외한다.

class Solution:
    def minimumObstacles(self, grid: List[List[int]]) -> int:
        dr = [-1, 1, 0, 0]
        dc = [0, 0, -1, 1]

        R = len(grid)
        C = len(grid[0])

        visit = defaultdict(int)

        q = [(0, 0, 0)]

        visit[(0, 0)] = 0

        while q:
            remove, row, col = heappop(q)

            for i in range(4):
                trow = row + dr[i]
                tcol = col + dc[i]
                if min(trow, tcol) < 0 or trow >= R or tcol >= C:
                    continue

                new_remove = remove + grid[trow][tcol]
                if (trow, tcol) not in visit or visit[(trow, tcol)] > new_remove:
                    visit[(trow, tcol)] = new_remove
                    heappush(q, (new_remove, trow, tcol))

        return visit[(R-1, C-1)]