Leetcode 3243. Shortest Distance After Road Addition Queries I

문제

class Solution:
    def shortestDistanceAfterQueries(self, n: int, queries: List[List[int]]) -> List[int]:
        dp = [0] * n

        graph = defaultdict(list)

        for i in range(n):
            dp[i] = i

        ans = []

        for start, end in queries:
            graph[start].append(end)

            dp[end] = min(dp[end], dp[start] + 1)

            if end in graph:
                for to in graph[end]:
                    dp[to] = min(dp[to], dp[end] + 1)

            for ee in range(end + 1, n - 1):
                dp[ee] = min(dp[ee], dp[ee - 1])
                if ee in graph:
                    for to in graph[ee]:
                        dp[to] = min(dp[to], dp[ee] + 1)

            dp[n - 1] = min(dp[n - 1], dp[n - 2] + 1)

            ans.append(dp[-1])

        return ans

• 0~n-1의 이름을 가진 도시가 있다.
• 각 도시는 0부터 n-1 까지 일직선으로 연결되어 있다.
• 쿼리는 아래를 의미한다.
  • [s, e]
    • s 도시에서 e도시로 가는 다리를 건설한다.
• 쿼리로 인한 다리가 계속 쌓여나간다고 할때, 각 쿼리마다 0번 도시에서 (n - 1) 번 도시로 갈때 최단 거리를 각각 구하시오

예시

n = 5, queries = [[2,4],[0,2],[0,4]]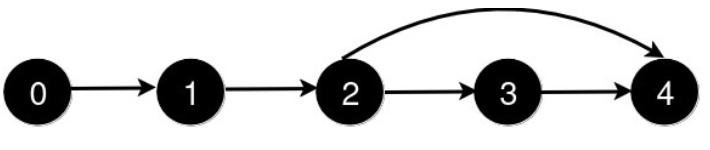

• 첫번째 다리가 놓아지면
• 0 -> 1 -> 2 -> 4 로 3번 이동

• 두번째 다리가 놓아지면
• 0 -> 2 -> 4 로 2번 이동

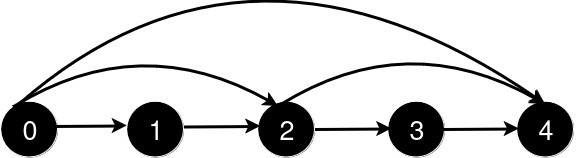
• 세번째 다리가 놓아지면
• 0 -> 4 로 1번 이동

답 : [3, 2, 1]

제한

• $3 <= n <= 500$
• $1 <= queries.length <= 500$
• $queries[i].length == 2$
• $0 <= queries[i][0] < queries[i][1] < n$
• $1 < queries[i][1] - queries[i][0]$
• 중복되는 다리는 존재하지 않는다.

풀이

• 1차원 DP를 이용해 푼다.
• DP의 각 원소의 뜻
  • 0번째부터 자신까지 가는 최소한의 거리

class Solution:
    def shortestDistanceAfterQueries(self, n: int, queries: List[List[int]]) -> List[int]:
        dp = [0] * n

        graph = defaultdict(list)

        for i in range(n):
            dp[i] = i

        ans = []

        for start, end in queries:
            graph[start].append(end)

            dp[end] = min(dp[end], dp[start] + 1)

            if end in graph:
                for to in graph[end]:
                    dp[to] = min(dp[to], dp[end] + 1)

            for ee in range(end + 1, n - 1):
                dp[ee] = min(dp[ee], dp[ee - 1])
                if ee in graph:
                    for to in graph[ee]:
                        dp[to] = min(dp[to], dp[ee] + 1)

            dp[n - 1] = min(dp[n - 1], dp[n - 2] + 1)

            ans.append(dp[-1])

        return ans