Leetcode 746. Min Cost Climbing Stairs with Python

문제

You are given an integer array cost where cost[i] is the cost of ith step on a staircase. 
Once you pay the cost, you can either climb one or two steps.

You can either start from the step with index 0, or the step with index 1.

Return the minimum cost to reach the top of the floor.

계단을 밟을때 사용하는 cost의 배열인 cost[i]가 주어집니다.
당신은 계단을 하나 혹은 두개씩 오를수 있습니다.
제일 높은곳에 도달하기 까지 사용되는 최소한의 cost를 계산하십시오.

예시

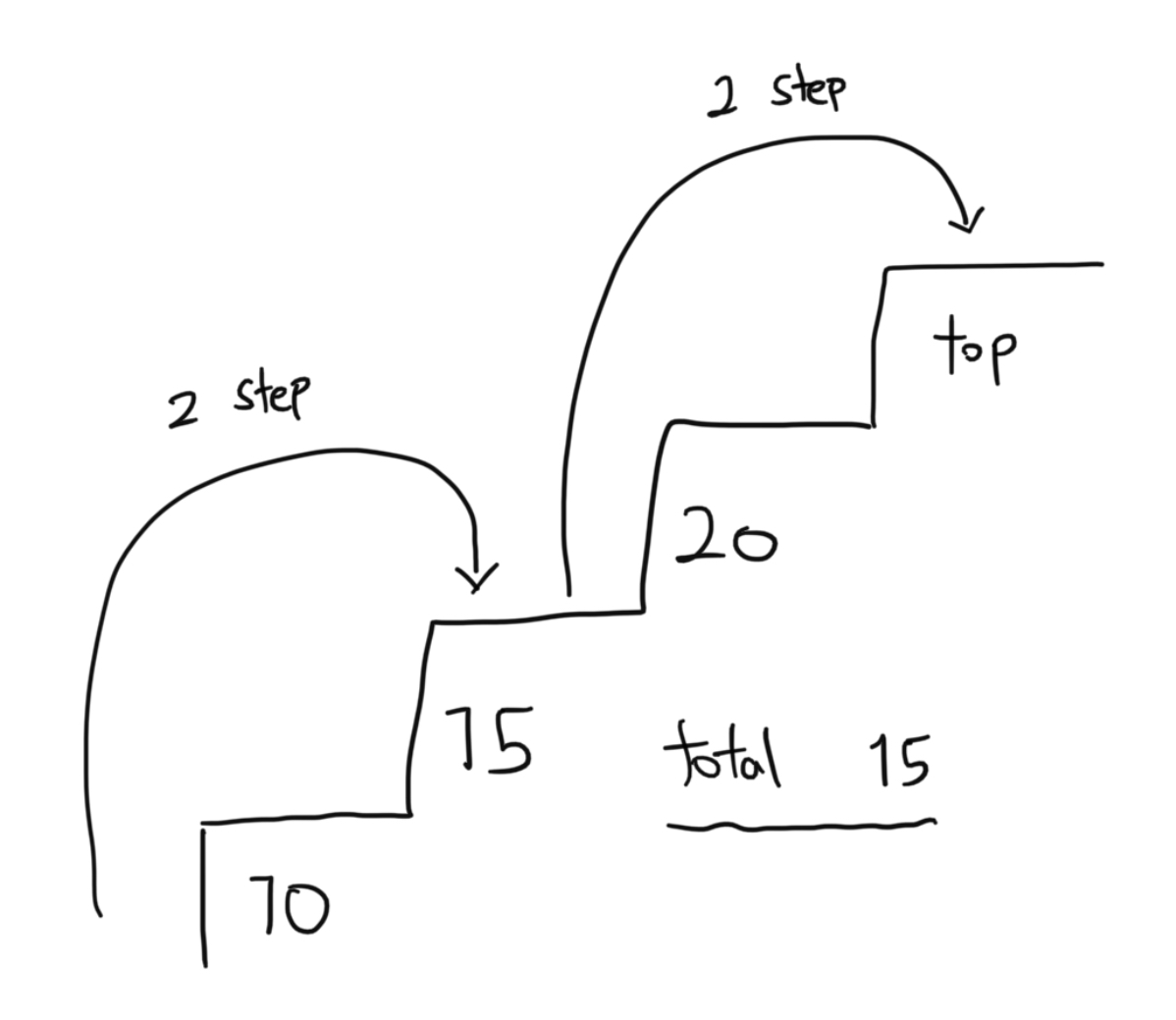
Input: cost = [10,15,20]
Output: 15
Explanation: 2계단 올라가 15 짜리 밟고 다시 2계단 올라가면 도착.

제한

• 2 <= cost.length <= 1000
• 0 <= cost[i] <= 999

풀이법

Dynamic programming의 memoization을 이용하면 빠른 속도 내에 풀수 있다.

dp 라는 이름의 배열을 하나 더 만들어 이용한다.

dp의 배열의 값은 각 dp index에 해당하는 계단까지 도달하는데 든 최소 비용을 의미하는데

dp[0] 과 dp[1]은 처음 올라가는 계단이기 때문에 cost[0]과 cost[1]이 그대로 들어가면 되고

0, 1번째 계단이 아닌 2번째 계단부터는 약간 복잡해지는데 별거 없다.

2번째 계단에 도달하기 위해선 0번째 계단에서 2계단을 올라가는 방법과 1번째 계단에서 1계단을 올라오는

두가지 방법밖에 없기 때문이다.

이 둘을 비교해 짧은 방법을 택하면 된다.

i번째 계단에 대해

dp[i-2] + cost[i] 와 dp[i-1] + cost[i] 를 비교하는 것이다.

이를 통해 끝까지 계산 후

마지막 최후까지 올라갈수 있는 경우는 dp의 맨 마지막 원소와 맨 마지막 바로 이전 원소이기에

이 둘중 최솟값을 리턴하면 된다.

class Solution:
    def minCostClimbingStairs(self, cost: List[int]) -> int:
        cost = cost
        dp = [0 for _ in range(len(cost))]
        dp[0] = cost[0]
        dp[1] = cost[1]
        for j in range(2, len(cost)):
            dp[j] = min(dp[j-2] + cost[j], dp[j-1] + cost[j])
        return min(dp[len(dp)-1], dp[len(dp)-2])

Recursive 하게 < Top - Down >

원리는 같다.

def rec(dp, cost, n):
    if n < 0: return 0
    if dp[n] != 0: return dp[n]
    dp[n] = min(cost[n] + rec(dp, cost, n-1), cost[n] + rec(dp, cost, n-2))
    return dp[n]

class Solution:
    def minCostClimbingStairs(self, cost: List[int]) -> int:
        dp = [0] * (len(cost))
        cost = cost
        dp[0] = cost[0]
        dp[1] = cost[1]
        return min(rec(dp, cost, len(dp)-1), rec(dp, cost, len(dp)-2))