
본 문서는 https://www.udemy.com/course/master-the-coding-interview-big-tech-faang-interviews/ 강의를 참조하여 작성되었습니다.
본 글은 강의 내용중 bellman-ford 알고리즘의 내용을 포함합니다.
문제
You are given a network of n nodes,
labeled from 1 to n.
You are also given times,
a list of travel times as directed edges times[i] = (ui, vi, wi),
where ui is the source node, vi is the target node,
and wi is the time it takes for a signal to travel from source to target.
We will send a signal from a given node k.
Return the minimum time it takes for all the n nodes to receive the signal.
If it is impossible for all the n nodes to receive the signal, return -1.n개의 1~n으로 라벨링 된 노드를 가진 정점들이 있습니다.
이들 사이의 간선은 times 배열에 [ui, vi, wi] 형태로 저장되어 있는데
ui는 시작정점, vi는 도착정점, wi는 신호가 지나가는데 걸리는 시간을 의미합니다.
k 노드로부터 신호를 보낼때, 모든 정점이 신호를 받을수 있으면, 전부 신호를 받는데 걸린 시간을
특정 노드는 신호를 받을수 없다면 -1을 리턴하세요.
예시
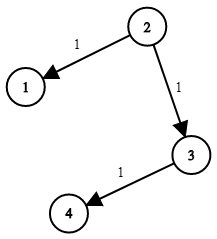
Input: times = [[2,1,1],[2,3,1],[3,4,1]], n = 4, k = 2
Output: 2제한
- 1 <= k <= n <= 100
- 1 <= times.length <= 6000
- times[i].length == 3
- 1 <= ui, vi <= n
- ui != vi
- 0 <= wi <= 100
- time에 주어지는 모든 간선은 unique 하다.
풀이법
1. Dijikstra
정점의 갯수만큼의 distance 배열을 만들어 시작 정점의 index를 제외하고 2**32라는 아주 큰 수로 채운다.
이는 시작 정점과 index에 해당하는 정점의 거리를 나타내는 것으로, 시작 정점 index는 자기 자신의 거리인 0이 된다.
이후 시작정점에서 연결되는 정점들의 거리로 distance를 갱신하고
distance와 크기가 같으면서 모든 값이 0인 check 배열을 만들어 시작정점 index의 값을 1로 만들어
시작 정점에서 근처의 점의 거리를 계산 했음을 적어 놓는다.
이후 distance의 최솟값을 가지면서 check값이 1이 아닌 index를 리턴하는 함수를 통해 시작 정점에서
제일 가까우면서 주변의 점의 거리를 측정해보지 않은 정점을 가져와
그 정점과 연결된 모든 간선을 확인하는데
index를 가져옴과 동시에 check에 표시를 해주는것이 중요하다!
본 시작정점이 p이고 도착 정점이 q이고 그 거리가 w일떄
distance[q], 즉 시작 정점에서 q까지의 거리보다 distance[p] + w, 즉 시작정점에서 p를 거쳐 q로 가는 거리가
짧을 경우 distance[q]를 본 값으로 대치한다.
만약 distance가 제일 짧으면서 연결되지 않은 index를 찾을수 없으면 종료되는데
distance에 여전히 2**32 라는 큰 숫자가 남아 있으면, 연결이 되어있지 않아 이 정점으로는 갈수 없었다는 의미이기에
-1을 리턴하고,
아니면 distance의 최대값을 리턴하면 된다.
코드는 아래와 같다.
class Edge:
def __init__(self, to: int, weight: int):
self.to = to
self.weight = weight
def getLeastDistance(check: List[int], distance: List[int]):
min = 2 ** 32
idx = -1
for i, v in enumerate(distance):
if min > v and check[i] == 0:
min = v
idx = i
return idx
class Solution:
def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
INF = 2 ** 32 + 1
graph = [list() for _ in range(n + 1)]
check = [0 for _ in range(n + 1)]
distance = [INF for _ in range(n + 1)]
reachable = n - 1
for t in times:
graph[t[0]].append(Edge(t[1], t[2]))
# 시작 정점 표 및 check
check[k] = 1
distance[k] = 0
for g in graph[k]:
distance[g.to] = g.weight
while True:
# distance가 짧으면서 check되지 않은 정점 찾기
start = getLeastDistance(check, distance)
# 없으면 break
if start == -1: break
# 있으면 check 해서 다시 뽑히지 않도록 방지
check[start] = 1
reachable -= 1
for v in graph[start]:
# 이미 정점 체크가 끝나지 않은 정점에 한해 거쳐 가는게 빠른지 직접 가는게 빠른지 비교 후 대치.
if check[v.to] == 0 and distance[v.to] > distance[start] + v.weight:
distance[v.to] = distance[start] + v.weight
distance = distance[1:]
if reachable == 0: return max(distance)
else: return -1
Bellman-ford 알고리즘
dijikstra보단 조금 느리지만 간선의 가중치 / 거리 가 음수인 경우에도 사용이 가능하다.
위와 같은 distance를 만들어 준 다음에
비교해서 대치하는거는 똑같은데, 여기서 다른점은 제일 작은 index를 뽑아 내려는 노력을 안한다.
그냥 정점의 갯수 - 1 번 동안 모든 간선에 대해 dijikstra와 같은 연산을 반복한다.
그러면 distance가 알아서 계산된다.
class Solution:
def networkDelayTime(self, times: List[List[int]], n: int, k: int) -> int:
INF = 2 ** 32
distance = [INF for _ in range(n+1)]
distance[k] = 0
for _ in range(n-1):
for edge in times:
if distance[edge[1]] > distance[edge[0]] + edge[2]:
distance[edge[1]] = distance[edge[0]] + edge[2]
distance = distance[1:]
try:
distance.index(INF)
return -1
except:
return max(distance)
### 압도적으로 짧은 소스코드
코드가 짧고 이해하기 쉽지만, 수행속도는 Dijikstra에 비해 2-3배정도 느리다.
