Leetcode 773. Sliding Puzzle

문제

On an 2 x 3 board, there are five tiles labeled from 1 to 5, and an empty square represented by 0. A move consists of choosing 0 and a 4-directionally adjacent number and swapping it.

The state of the board is solved if and only if the board is [[1,2,3],[4,5,0]].

Given the puzzle board board, return the least number of moves required so that the state of the board is solved. If it is impossible for the state of the board to be solved, return -1.

• 2 x 3 슬라이딩 퍼즐에 1~5까지의 블록이 꽂혀 있다.
• 0이 의미하는것은 빈 부분을 의미하며, 이는 주변의 다른 블록과 위치를 바꿀수 있다.
  • 즉, 빈자리로 다른 블록이 이동한다.
• [1, 2, 3][4, 5, 0] 이 되면 풀어졌다고 가정할때, 풀때까지의 최소한의 움직임을 구하거나
• 안된다면 -1을 리턴하시오.

예시

• 5를 왼쪽으로 옮기면 끝이니까 1!

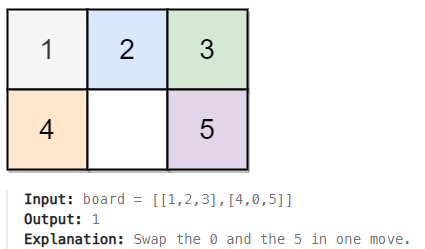
제한

• $board.length == 2$
• $board[i].length == 3$
• $0 <= board[i][j] <= 5$
• 보드 내 모든 값은 유일하다. ( 1 ~ 5 )

풀이법

• 일단 2X3 밖에 되지 않는 사이즈이기 때문에 BFS를 통해 모든 경우의 수를 탐색할수 있다.
• 단! 이미 탐색한 경우의 수는 visited set을 통해 걸러 주어야 빠르게 구할수 있다.
• queue를 이용한 BFS를 구현해 해결할수 있었다.

class Solution:
    def slidingPuzzle(self, board: List[List[int]]) -> int:
        dr = [-1, 1, 0, 0]
        dc = [0, 0, -1, 1]

        q = deque()

        visited = set()

        q.append((board, 0))

        while q:
            board_state, step = q.popleft()

            if board_state == [[1, 2, 3], [4, 5, 0]]:
                return step

            r = 0
            c = 0

            for i in range(6):
                if board_state[i // 3][i % 3] == 0:
                    r = i // 3
                    c = i % 3
                    break

            for i in range(4):
                tr = r + dr[i]
                tc = c + dc[i]
                if tr < 0 or tc < 0 or tr >= 2 or tc >= 3:
                    continue

                moved_board = [[num for num in row] for row in board_state]
                moved_board[tr][tc], moved_board[r][c] = moved_board[r][c], moved_board[tr][tc]

                if str(moved_board) not in visited:
                    visited.add(str(moved_board))
                    q.append((moved_board, step + 1))

        return -1

후기

• 점심시간에 푸려고 했을땐 컨디션이 안좋아서 되도 안하는 게임이론 같은거 생각하고 있었는데
  생각해보니 이정도 사이즈면 그냥 BFS로 선택트리처럼 하면 되는거 아닌가? 싶어서 해보니
  되네? 어??