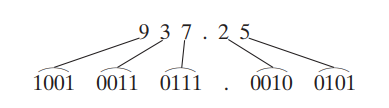논리회로 Ch1. Introduction to Number system and Conversion

1.1 Digital System and Switching Circuit

Logic Circuit

Logic Circuit은 AND, OR, NOT과 같은 Logic gate들로 이루어진다.

Combinational circuit

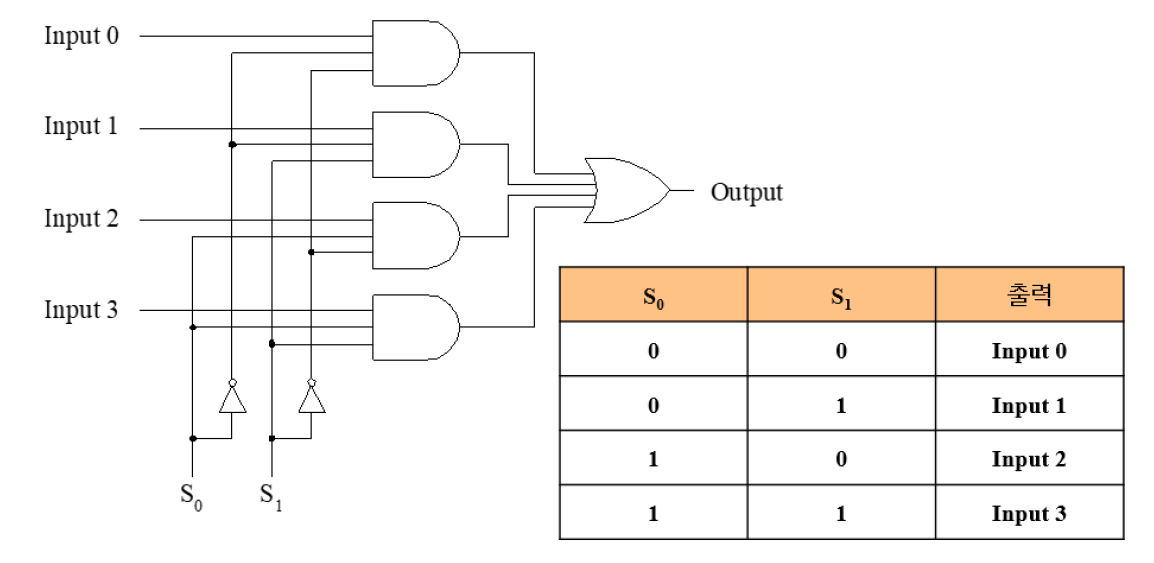
출력이 오직 입력에만 영향을 받는다.

즉, 입력이 같다면 출력은 항상 같다.

• 예시 : 전가산기

Sequential circuit

출력이 입력과 이전 출력에 의해 결정된다.

이전의 출력은 state ( 상태 ) 로 회로에 저장된다.

• 예시 : Flip-Flop

---

1.2 Number Systems and Conversion

모든 진법에서 소숫점 아래의 숫자는 n이 음수가 된다.

2진법에서 0.1은 $2^{-1} * 1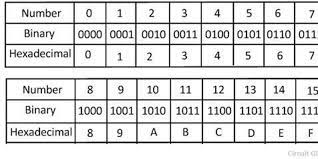$과 같다

1. Decimal Number, 10진법

• 10^n * a 값들의 덧셈으로 이루어진다. $0 <= a < 10$
  예시 : $1234=10^3\times1+10^2\times2+10^1\times3+10^0\times4$

2. Binary number, 2진법

• 2^n * a 값들의 덧셈으로 이루어진다. [ 0 <= a < 10 ]
  예시 : $1011 = 2^3 \times 1 + 2^2 \times 0 + 2^1 \times 1 + 2^0 \times 1$

10진법과 2진법을 서로 변환하는 방법

• 10진법 -> 2진법

  • 2로 나누어가며 나오는 나머지를 통해 구할수 있다.
    

  • 증명

    2진법은 2^n * a들의 합으로 이루어져 있는데, 
    이 값에 2를 나누게 되면 n이 0이 아닌 나며지는 n으로 나누어져 몫을 가지지만
    n이 0인 부분은 몫이 없어 그대로 나머지가 된다.
    즉 n이 0인 a값들을 하나하나 추출해 내는 방식이다.
    
    2^3 * 1 + 2^2 * 0 + 2^1 * 1 + 2^0 * 1 을 2로 나누면
    1이 나머지가 되고
    2^2 * 1 + 2^1 * 0 + 2^0 * 1
    이 몫이 된다.

• 2진법 -> 10진법
  • 곱셈과 덧셈으로 $2^n \times a$를 계산하면 된다.

소숫점 아래 2진수를 10진수로 변환하는 방법

• 예시 : $0.101_2$
  • 방법

0.101은 풀어서 작성하면 아래와 같습니다.
2^-1 * 1 + 2^-2 * 0 + 2^-3 * 1
이 숫자에 2를 곱하면 맨 앞의 항이 2^0 * 1이 되어 소수점 밖으로 나오게 됩니다.
이렇게 소수점 밖으로 나온 숫자들을 하나하나 모아 나가면서 구하면 됩니다.

3. Hexadecimal Number, 16진법

• 2^n * a 값들의 덧셈으로 이루어진다. $0 <= a < 16$

• 2진법의 4자리를 묶으면 16진법의 한 자리와 대응한다.

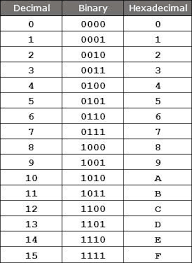
• 10진수로 표현 불가능한 부분은 A~F로 표기한다.

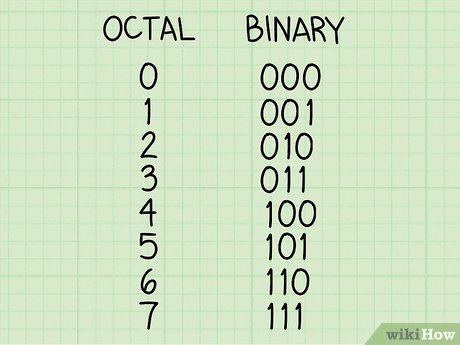
4. Octal Number, 8진법

• 2^n * a 값들의 덧셈으로 이루어진다. $0 <= a < 8$

• 2진법의 3자리를 묶으면 16진법의 한 자리와 대응한다.

---

1.3 Binary Arithmetic

이진수끼리 사칙연산이 가능하다.

1. 덧셈
   

• Carry = 올림수

2. 뺄셈
   

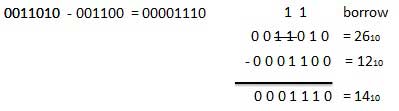
• Borrow = 빌림수
• 빌림수를 표현시 2진수로 10으로 표현한다, 이는 10진수로는 2와 같은 숫자이다.

3. 곱셈
   

• 이후 나올 곱셈기는 이 원리를 적극 활용한다.

3. 나눗셈
   

• 이후 나올 나눗셈기는 이 원리를 적극 활용한다.

---

1.4 Representation of Negative Numbers

1. Sign and Magnitude Numbers

부호 절대값

MSB에 부호에 대한 정보를 담는다.

• MSB가 0이면 양수, 1이면 음수가 된다.
• MSB를 제외한 비트는 숫자 크기의 절댓값이 된다.

+	2진수	-	2진수
0	0000	-0	1000
1	0001	-1	1001
2	0010	-2	1010
3	0011	-3	1011
4	0100	-4	1100
5	0101	-5	1101
6	0110	-6	1110
7	0111	-7	1111

• 이를 사용해 숫자를 계산하는 회로를 설계하는것은 어렵다

2. 2's Complement number

2의 보수

비트를 전부 Flip 하고 1 더한다.

• MSB가 0이면 양수이고 1이면 음수이다.

+	2진수	-	2진수
0	0000	-0	X
1	0001	-1	1111
2	0010	-2	1110
3	0011	-3	1101
4	0100	-4	1100
5	0101	-5	1011
6	0110	-6	1010
7	0111	-7	1001
8	X	-8	1000

• n 비트로 표현하는 숫자 N에 대해 N의 2의 보수는 2^n - N과 같다.

  • N과 더했을때 $2^n$이 되는 숫자

• 예를 들어 4비트로 표현한 숫자 0010에 대해 N의 보수는 10000 - 0010이 되는것이다.

	10000 - 0010
=   1111 + 1 - 0010
=   (1111 - 0010) + 1

• 이는 풀어서 작성하면 (1111 - 0010) + 1과 마찬가지가 되는데, 앞부분이 모든 Bit를 Flip하고, 뒷부분은 1을 더하는 모양새가 된다.

• 2의 보수를 이용해 2진법의 뺄셈을 계산할수 있다.
  • 10의 보수를 이용해 10진법의 뺄셈또한 계산 가능.

2의 보수의 덧셈

양수 + 양수

• 덧셈 결과로 음수가 나올수도 있는데, 이는 결과가 표기가능한 양수의 범위를 넘어선 경우이다.
  • 오버플로우

1. 올바른 양수와 양수의 덧셈 표기 가능한 양수 범위인 1 ~ 7을 넘기지 않는 결과.
   
2. 틀린 양수와 양수의 덧셈 표기 가능한 양수 범위인 1 ~ 7을 넘긴 결과.
   - 해결법 : 더 많은 비트를 사용해 숫자를 표현한다.
   

음수 + 음수

• 2의 보수로 표현된 음수를 그대로 덧셈 계산으로 더하면 된다
• 표기 가능한 비트보다 더 긴 결과가 나올수도 있는데, 이 경우 MSB쪽의 비트를 버리면 된다.
• 덧셈 결과로 양수가 나올수도 있는데, 이는 결과가 표기가능한 음수의 범위를 넘어선 경우이다.
  • 오버플로우

1. 크기를 넘기지 않는 음수와 음수의 덧셈

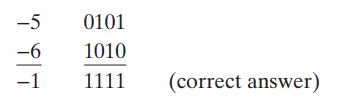
2. 크기를 넘기는 음수와 음수의 덧셈

3. 올바르지 않는 결과가 나오는 음수와 음수의 덧셈

양수와 양수를 더했는데 음수가 나오거나, 음수와 음수를 더했는데 양수가 나오면

그 연산은 오버플로우가 생긴것이다.

양수와 음수의 덧셈

• 양수와 2의 보수로 생긴 음수를 더하면 된다.
• 표기 가능한 비트보다 더 긴 결과가 나올수도 있는데, 이 경우 MSB쪽의 비트를 버리면 된다.

3. 1's Complement

1의 보수 표기

비트를 전부 Flip 한다.

• n자리 이진수로 표기되는 2진수 N에 대해 $(2^n - 1) - N$ 이 된다.

• MSB가 0이면 양수, 1이면 음수이다.

+	2진수	-	2진수
0	0000	-0	1111
1	0001	-1	1110
2	0010	-2	1101
3	0011	-3	1100
4	0100	-4	1011
5	0101	-5	1010
6	0110	-6	1001
7	0111	-7	1000

1의 보수 표기법에서의 연산은 2의 보수 표기법과 동일하다

하지만, 1의 보수 표기법에서 결과가 표현 가능한 범위를 초과하지 않으나 MSB에 비트가 더 많을경우 이를 버리지 않고 1의 자리로 옮겨 더해주면 된다.

• 크기가 초과하지 않는 경우
  • 평범하게 계산하면 된다.

• 크기가 초과하는 경우

  • 초과한 비트를 LSB 자리에 옮겨 더하면 된다.

    

• 물론 1의 보수 표기법으로 표현 가능한 범위를 넘어서 오버플로우가 발생할수도 있다.