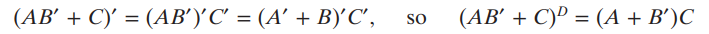논리회로 Ch2. Boolean algebra

Alpha, Orderly·2023년 3월 3일

논리회로

목록 보기

2/12

2.1 Introduction

1847년 George Boole이 수학 논리문제 해결을 위해 개발함
우리가 사용할 Boolean variable은 0 혹은 1의 값을 가집
이들은 숫자적 값(Numeric value)를 가지진 않음
논리회로에서 주로
- 0 : 저전압
- 1 : 고전압
을 나타냄
이 외에도 Binary valued system에서 0과 1은 많은것을 표현하는데 사용 가능.

두 값을 갖는 부울 대수는 종종 스위칭 대수(Switching Algebra)라고 불린다.

2.2 Basic Operations

NOT

Switching Algebra를 Switching circuit에 사용하기 위해 각각의 스위치를 variable로 이름붙힌다.

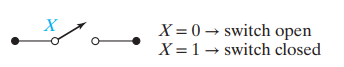
스위치가 열려있으면 0, 닫혀있으면 1

스위치의 닿는 부분(contact)은 Normally Open/NO/0 이거나 Normally Closed/NC/1이다.
스위치의 위치가 바뀌면 이들이 서로 바뀌게 된다.
이는 NO와 NC의 상태는 서로 반대라는 것이고, NO와 NC는 서로 보수(Complement)관계이다.
고로 Switching Algebra에서 0의 Complement는 1이 된다.

$0' = 1$ $and$ $1' = 0$
$X' = 1$ $if$ $X = 0$
$X' = 0$ $if$ $X = 1$

또한 스위치의 상태를 두번 바꾸면 다시 원래 상태로 돌아온다
보수의 보수는 다시 자기 자신이 된다.

$X'' = X$

Complementation의 다른 이름은 Inversion이며, 전자 회로에서 Inversion을 일으키는것은 보통 inverter라고들 부른다.
Inverter는 회로에서 다음과 같이 표현한다.

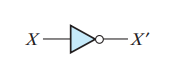
출력이 반대가 되는것(Inverted) 을 확인할수 있다

AND

2개의 스위치기 직렬로 연결되어 있을때 두 스위치가 모두 닫혀야 회로가 닫힌다.

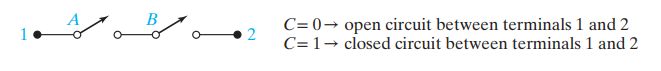
위는 진리표로 표현시 다음과 같다.

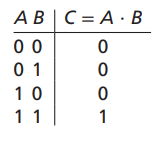
또한 위를 불대수로 작성시 아래와 같은 형태를 가진다.

$F = AB$

OR

2개의 스위치가 병렬로 연결되어 있을때 둘중 하나의 스위치만 닫혀도 회로가 닫힌다.

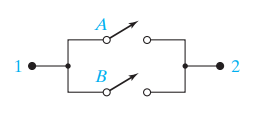
이를 진리표로 표현시 다음과 같다.

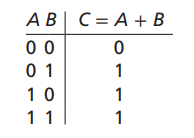
또한 위를 불대수로 작성시 아래와 같은 형태를 가진다.

$F = A + B$

OR는 Inclusive OR이라 불리기도 한다. Exclusive OR 또한 존재한다.

Logic Gate

Logic Gate에서 AND는 아래와 같이 표현된다.

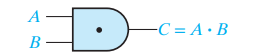
Logic gate에서 OR은 아래와 같이 표현된다.

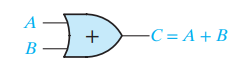
2.3 Boolean Expressions and Truth table

Boolean expression은 간단한 연산과 하나 혹은 더 많은 변수 혹은 상수로 이루어진다.
- 단일 상수 혹은 단일 변수 또한 Boolean expression이다.
여러 AND와 OR과 NOT을 사용해 복잡한 수식을 만들수도 있다.

$AB' + C$

* 이를 회로로 표현시 아래와 같다.

$[A(C + D)]' + BE$

* 이를 회로로 표현시 아래와 같다.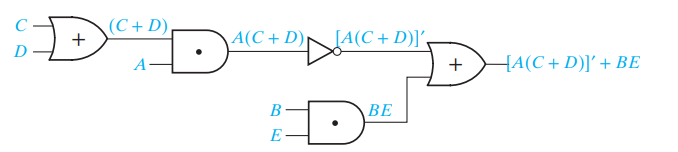

괄호는 주로 연산이 실행되는 순서를 명확하게 표기할때 사용된다.
위 연산들은 주로 변수를 0이나 1로 치환해 계산할수 있다.

진리표 / Truth Table

모든 가능한 변수 값의 경우의 수와 이에 따르는 Output 값을 정리해둔 것이다.
적는 순서는 정해진것이 없다.
n개의 변수에 따라 $2^n$ 개의 Row를 가진다.

$A' + B$ 의 진리표

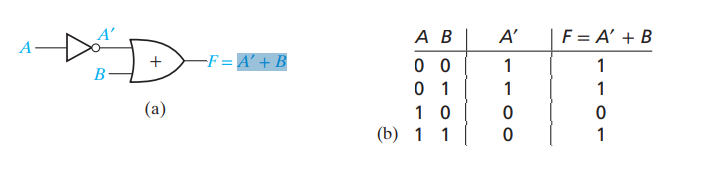
2.4 Basic Theorem

Boolean Algebra에서 반드시 알아야할 Theorem들.

Calculation with 0 and 1

$X + 0 = X$

$X + 1 = 1$

$X · 1 = X$

$X · 0 = 0$

Idempotent Laws

$X + X = X$

$X · X = X$

Involution Law

$(X')' = X$

Laws of Complementarity

$X + X' = 1$

$X · X' = 0$

각각의 법칙은 모든 가능한 변수에서 되는지 테스트함으로 확인 가능하다

2.5 Advanced Theorem

Commutative, Associative, Distributive, De-Morgan

Commutative law

$XY = YX$

$X + Y = Y + X$

AND 와 OR은 연산 순서 상관없이 같은 결과를 가진다.

Associative law

$(X + Y) + Z = X + (Y + Z) = X + Y + Z$

$(XY)Z = X(YZ) = XYZ$

AND에는 3개 이상의 input이 들어갈수 있다.

Distributive law

$X(Y + Z) = XY + XZ$

$X + YZ = (X + Y)(X + Z)$

DeMorgan law

$(X + Y)' = X'Y'$

$(XY)' = X' + Y'$

Duality

어떤 식이 있을때 그 식의 Dual 식도 항상 성립한다.
- 변수는 그대로 둠
- AND <> OR 변환
- 0 <> 1 변환
```
	   X(X+Y) = X
    -> X+XY = X
       성립한다.
       식의 양쪽을 둘 다 변환해야 한다!
```

2.6 Simplification Theorem

Uniting

$XY + XY'$
-> $X(Y + Y')$
-> $X$

$(X + Y)(X + Y′)$
-> $X + YY'$
-> $X$

Absorption

$X + XY$
-> $X(1+Y)$
-> $X$

$X(X + Y)$
-> $XX + XY$
-> $X + XY$
-> $X$

Elimination

$X + X′Y = X + Y$

$X(X′ + Y ) = XY$
-> $0 + XY$

Consensus / 동의, 합의

$XY + X'Z + YZ$
-> $XY + X'Z + (X+X')YZ$
-> $XY + X'Z + XYZ + X'YZ$
-> $XY + XYZ + X'Z + X'ZY$
-> $XY + X'Z$

$(X + Y)(X' + Z)(Y + Z) = (X + Y)(X' + Z)$

위 법칙들을 적용시 여러 변수로 이루어진 값을 일정 변수로 치환해 사용할수도 있다.
- 예시
  
  $Z = [A+B'C+D+EF][A+B'C+(D+EF)'] = [X+Y][X+Y'] = X = (A+B'C)$
  $X = (A+B'C)$
  $Y = (D+EF)$

2.7 Multiplying Out and Factoring

Factoring : 인수분해
Multiplying out : 거꾸로 전개하는것

Sum of product form / SOP

	AB + CD == Sum of product
    AB + D'EF + AD == Sum of product
    (A+B)C + D != Sum of product
    * 식을 풀어서 Sum of product form 으로 만들수도 있다.

Product of sum form / POS

    모든 합의 항은 단일 변수들의 합이여야 한다.
    (A+B)(C+D) == Product of sum
    (AB + CD)(D + E) != Product of sum
    * 식을 풀어서 Product of sum form 으로 만들수도 있다.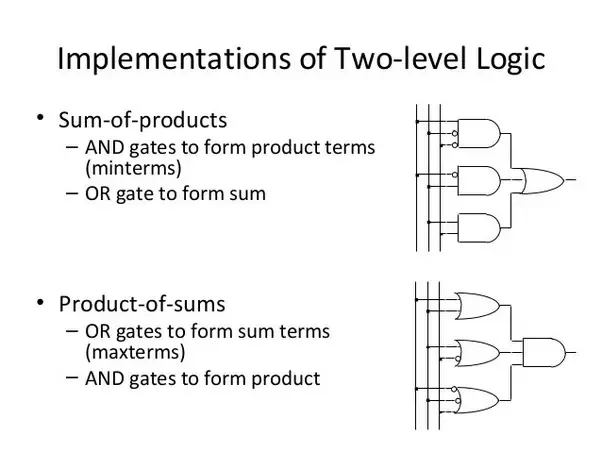

2.8 Complementing Boolean Expression

DeMorgan law에 따라 아래 식들이 성립한다.

$(X_1 + X_2 + X_3 + · · · + X_n)' = X_1'X_2'X_3' . . . X_n'$

$(X_1X_2X_3 . . . X_n)' = X_1'+ X_2'+ X_3'+ · · · + X_n'$

이를 이용해 보수의 식을 간소화 하는데 사용할수 있다.

Dual of expression이 전체 표현식의 보수를 구하면서 발견될수 있는데
이것은 모든 AND와 OR을 바꾸고 0과 1을 바꾸고 변수를 보수로 바꿈으로 생겨난다.

Alpha, Orderly

만능 컴덕후 겸 번지 팬

이전 포스트

논리회로 Ch1. Introduction to Number system and Conversion

다음 포스트