Simple fixed point iteration
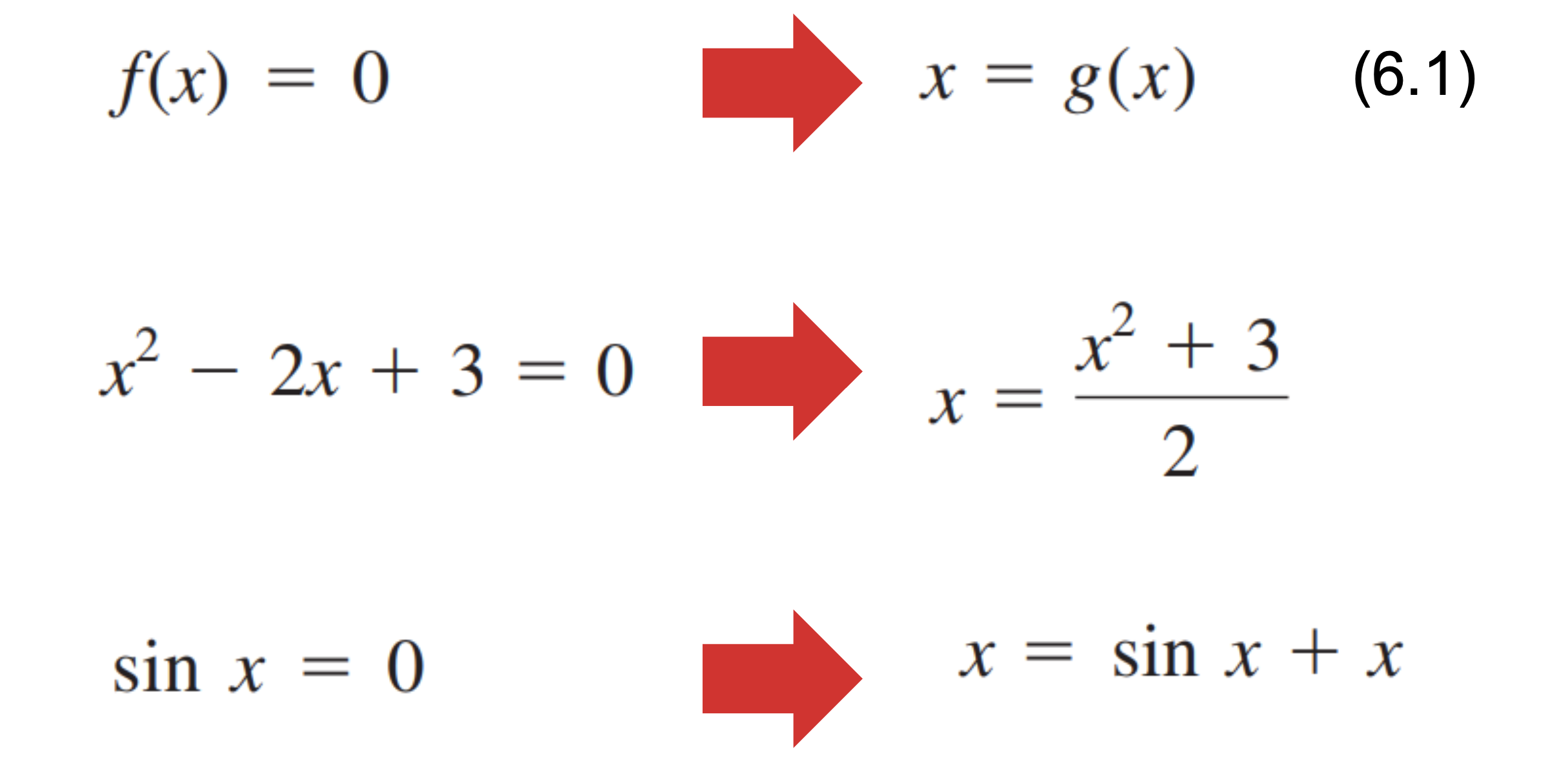
Fixed point
- 함수에 대해 자기 자신으로 매핑되는 원소.
- 상수 c에 대해 인 경우
- Domain 과 Co-domain 에 c가 모두 속한다.
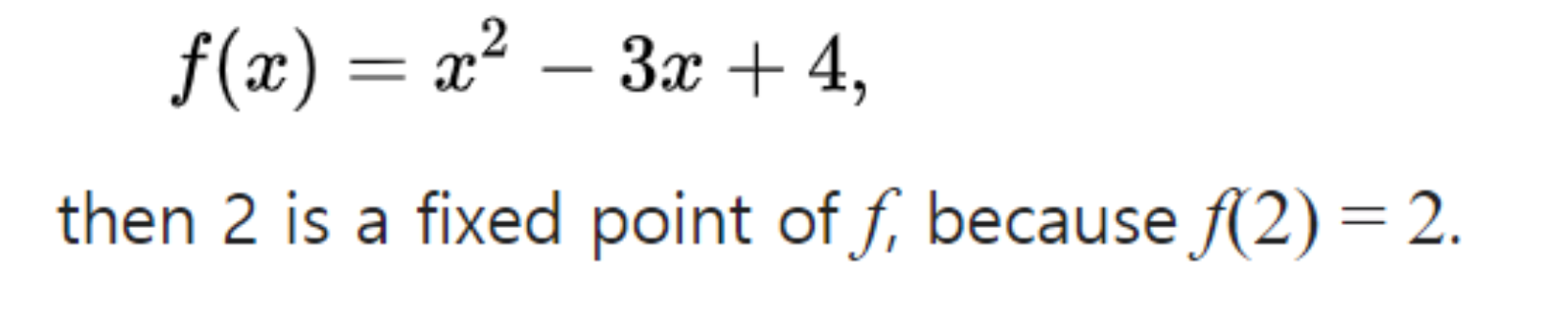

- Domain 과 Co-domain 에 c가 모두 속한다.
- 만나는 점들이 Fixed Point 가 된다.
- 모든 함수가 Fixed point를 가지진 않는다.
- Ex.
예시
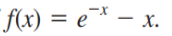
- 위의 근을 구하기
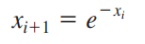
1. 형태로 변환하기
- 새로이 구한 은 다시 에 대입.
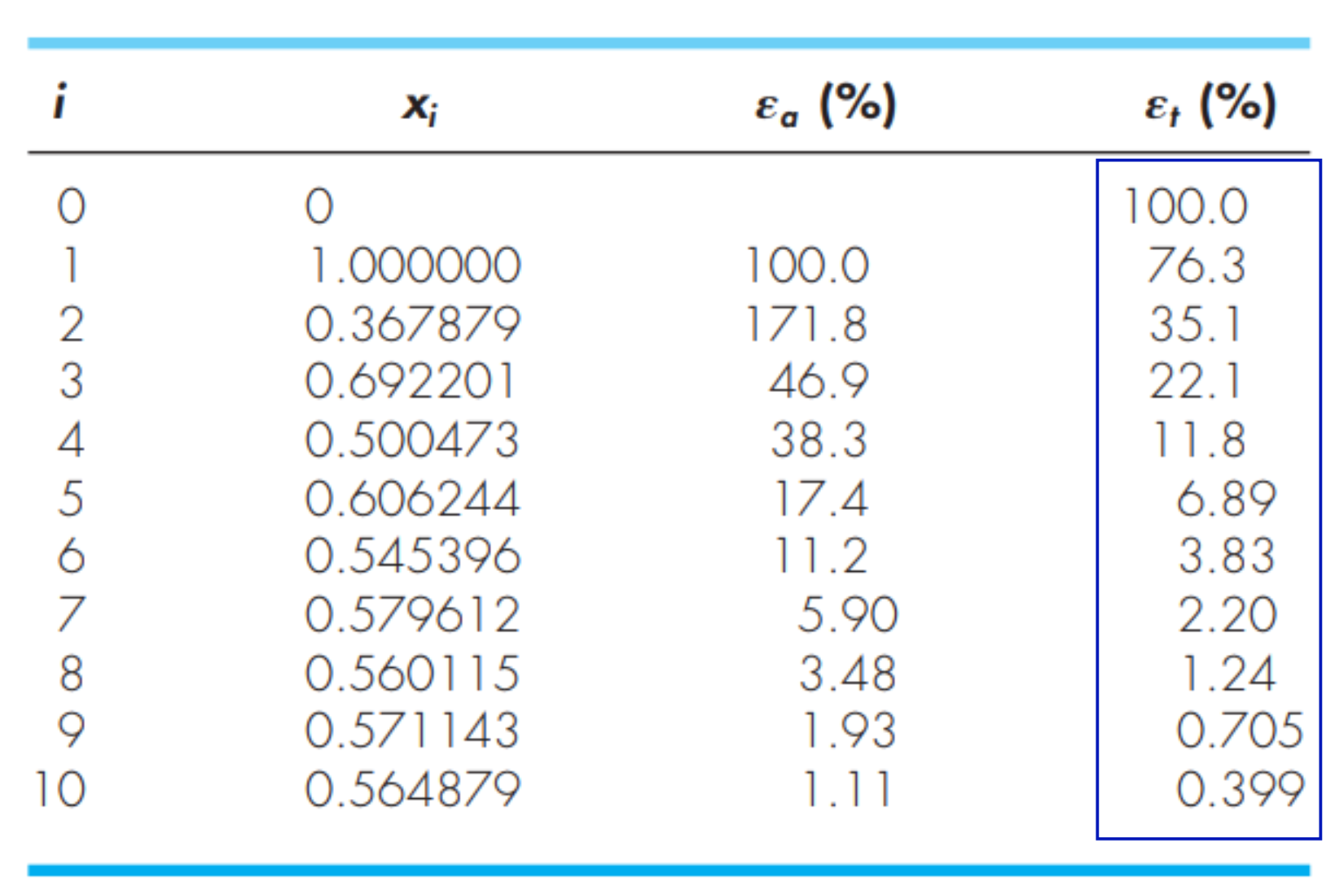
2. 부터 시작해 위 식을 반복한다.
- 에서 시작해 근을 찾는 과정
- 아래 경우 은 0부터 시작한다.
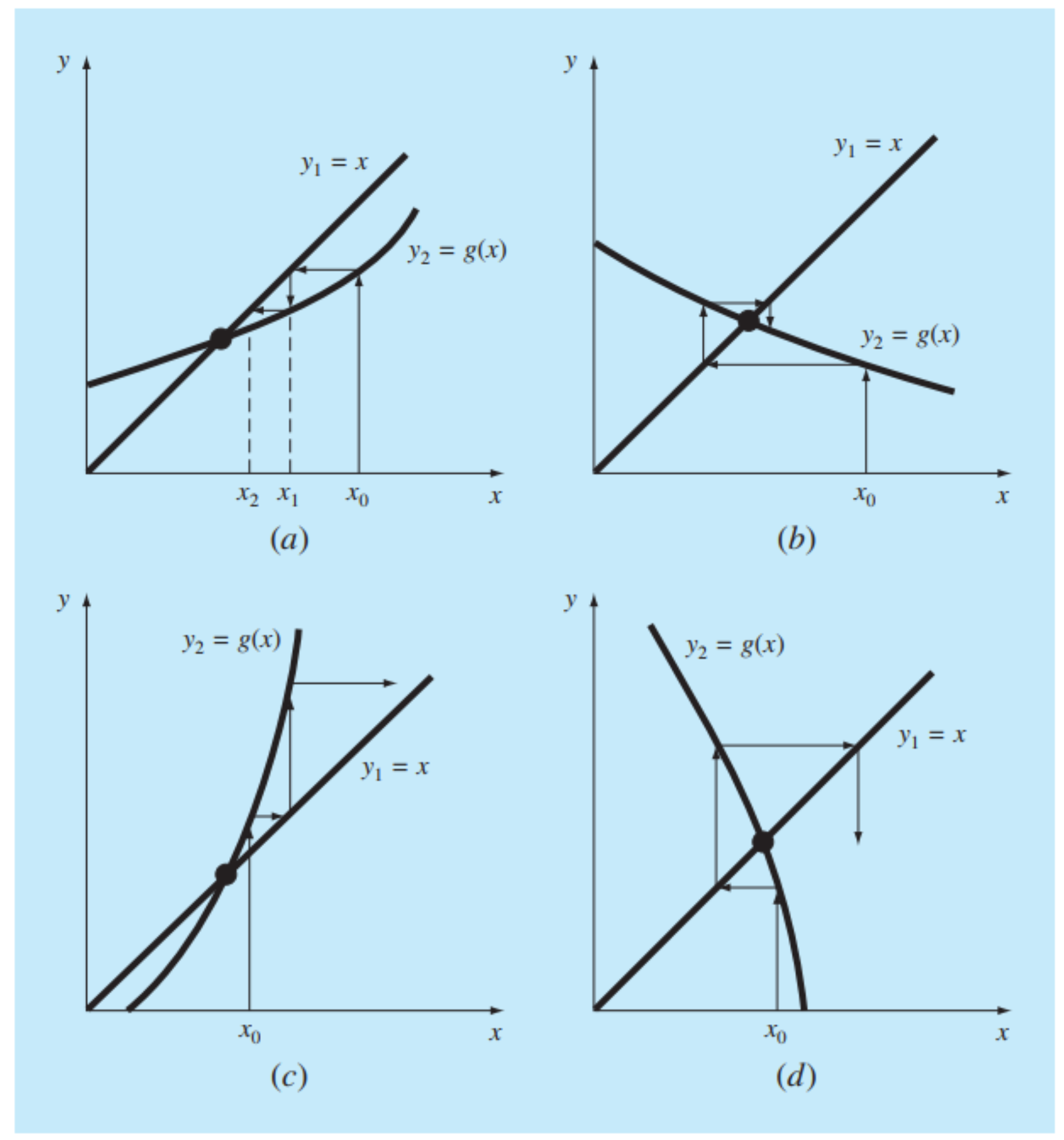
- (c), (d) 의 경우처럼 발산할수도 있다.
Newton-Raphson Method
- 미분과 이를 통해 구한 기울기를 사용한다.
- 즉, 수치해석적 미분이 아닌 미분식을 구해 사용한다.
- 를 반복한다.
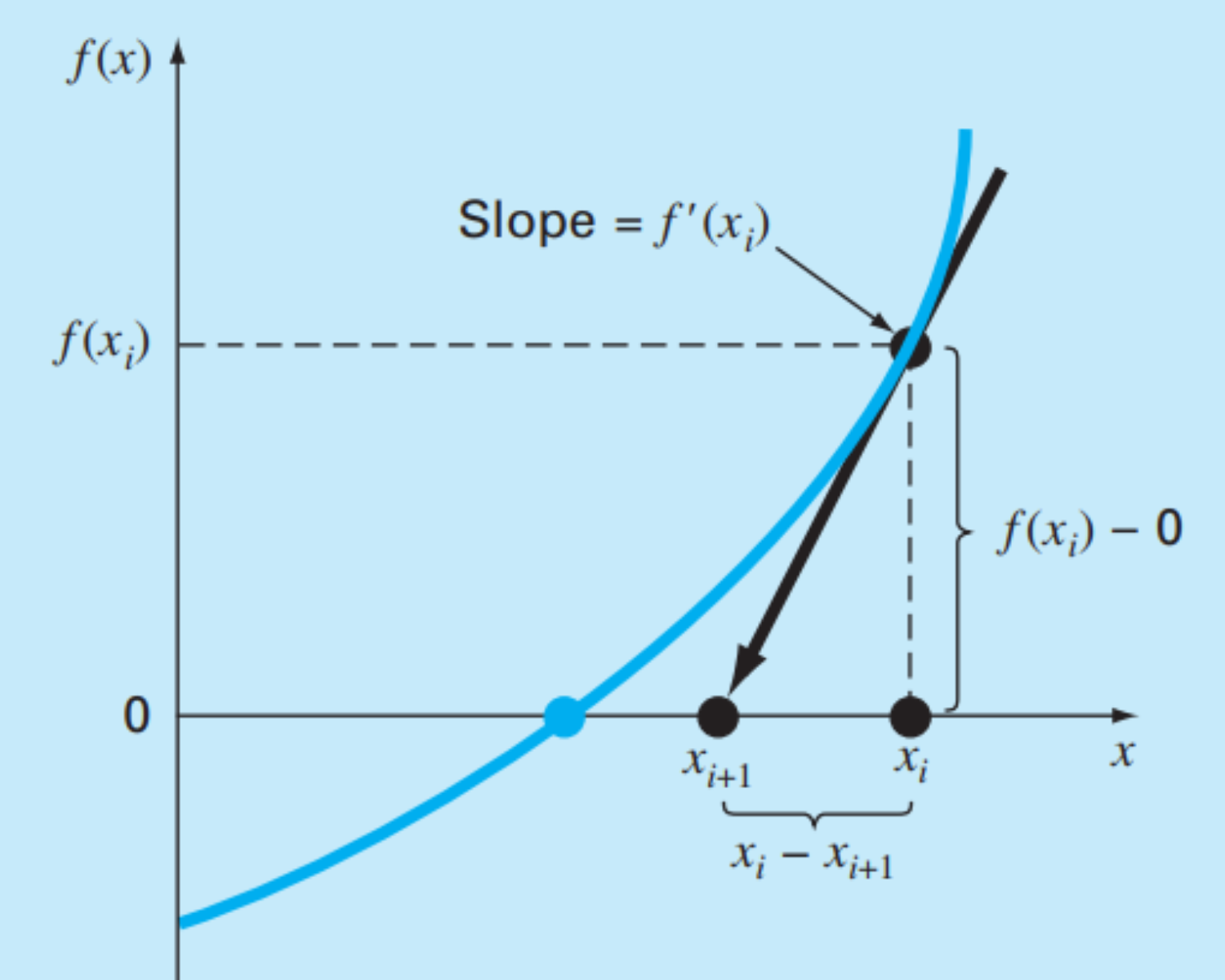
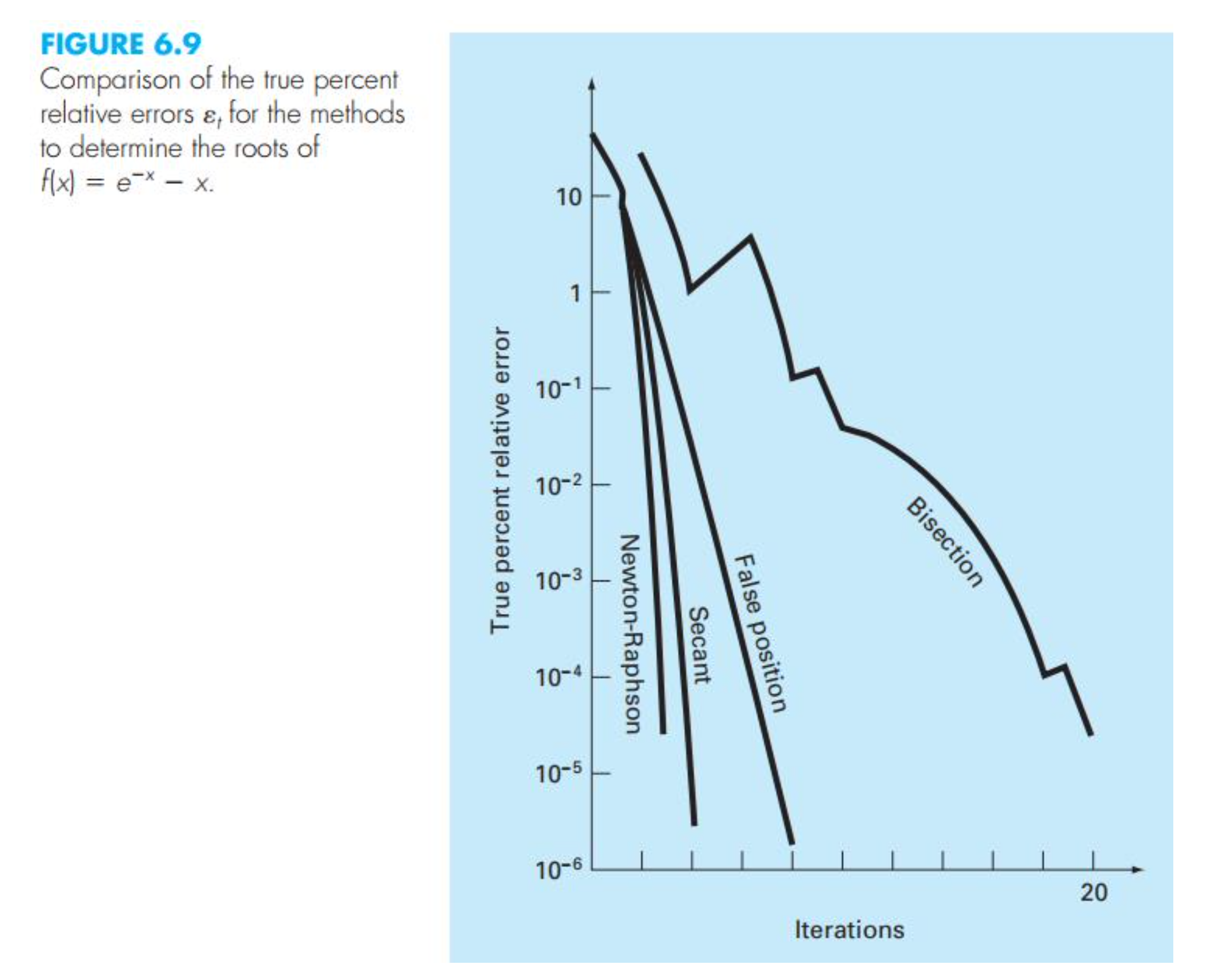
- 매우 빠르게 근에 접근한다.
- 하지만 과 같은 경우는 근을 빨리 찾지 못한다.
Secant Method
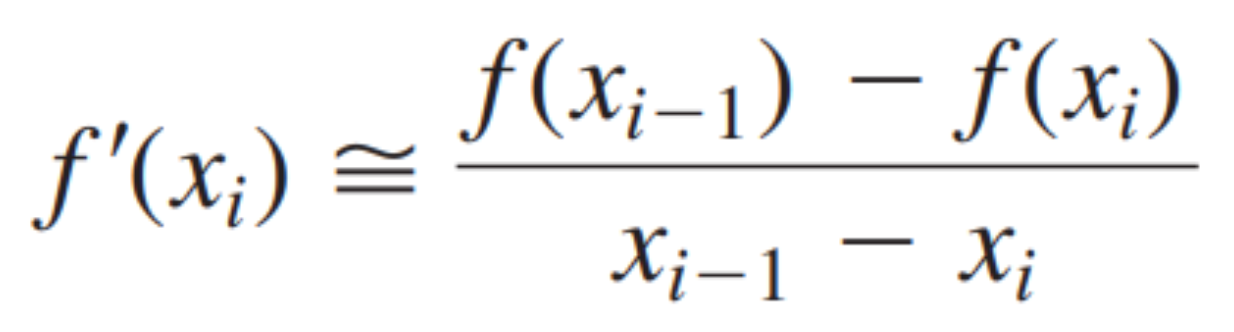
- 뉴튼 렙슨 방식에서 미분을 수치해석적으로 구한다.
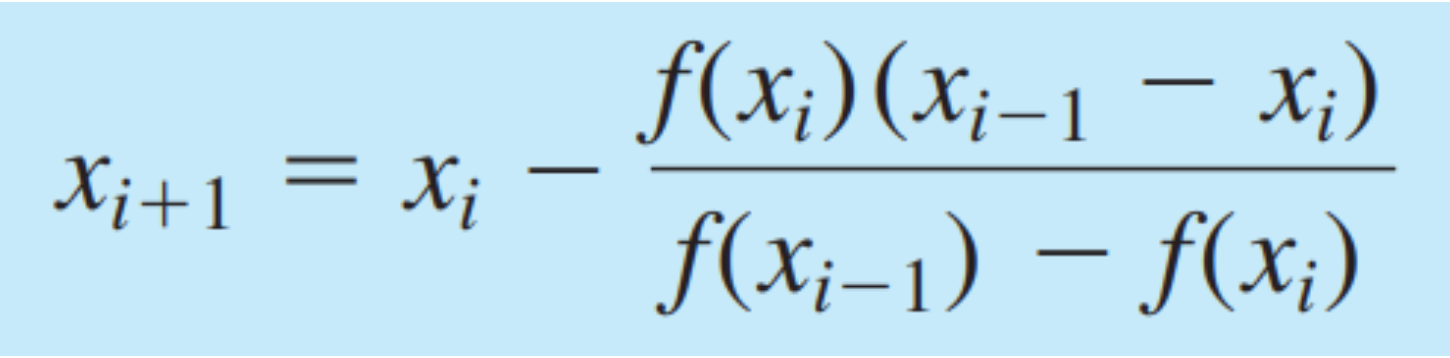
Modified Secant Method
- 수치 미분을 구할때, 값을 매우 작게 둔다.
- 이전 x값과 현재 x값을 사용해 기울기를 구한다.

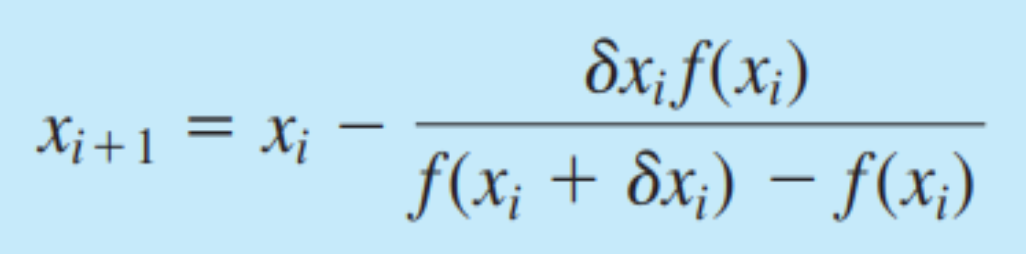
Brent Method
- CH5와 CH6의 방식을 조건에 따라 사용하는것.
- 정해진 구간을 벗어날 시 Bisection 사용, 범위 내에 있으면 CH6의 방식을 사용한다.
