최적화 / Optimization
- 함수의 최댓값, 최솟값을 찾는것
찾아내기
- 그 지점에서의 미분값이 0인 지점
- 2차 미분값이 0보다 크면 최솟값, 2차 미분값이 0보다 작으면 최대값이다.
Objective Function
- 최소값, 최대값을 찾으려는 함수
Multimodal Function
- 1개를 초과하는 최소, 최대값을 가지는 함수
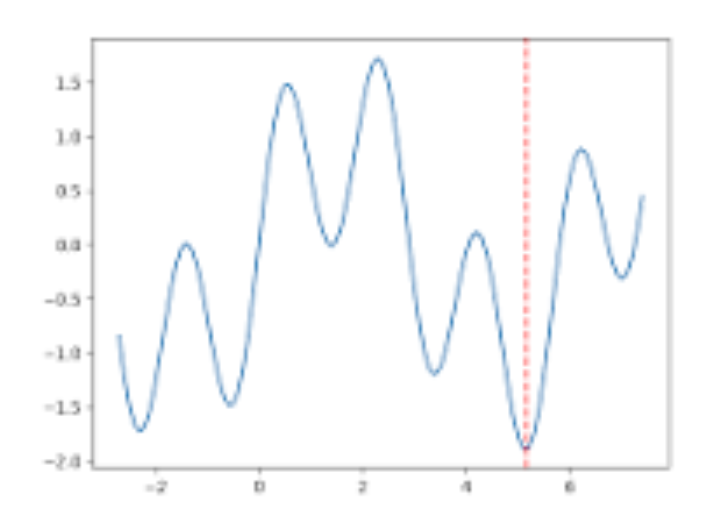
- 가장 높은 지점 : Global Maximum
- 가장 낮은 지점 : Global Minimum
- 최대 값 : Local Maximum
- 최소 값 : Local Minimum

Global Maximum/Minimum 을 찾는 방법
- 최대/최소 값을 찾아나가며 계속 Global 값을 설정한다.
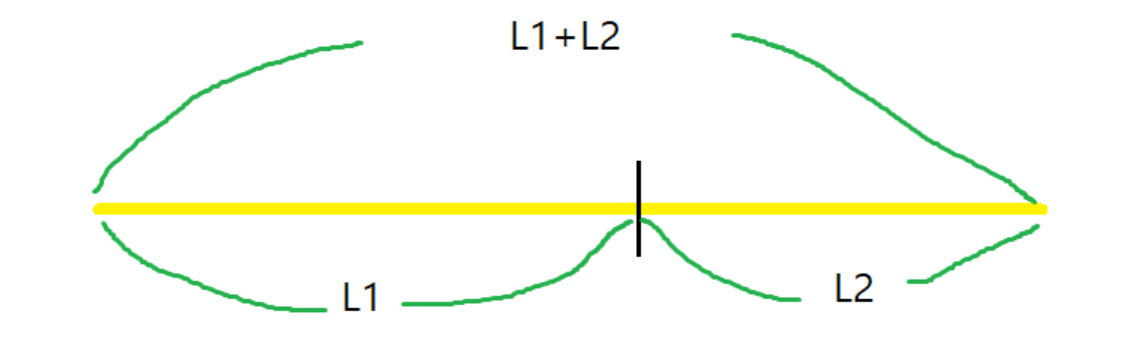
황금비
두 길이 에 대해 를 만족하면 과 는 황금비 를 가진다.
값은 대략 1.618
Golden Section Search
• The key is making this approach efficient by choosing
intermediate points wisely thus minimizing the function
evaluations by replacing the old values with new values.
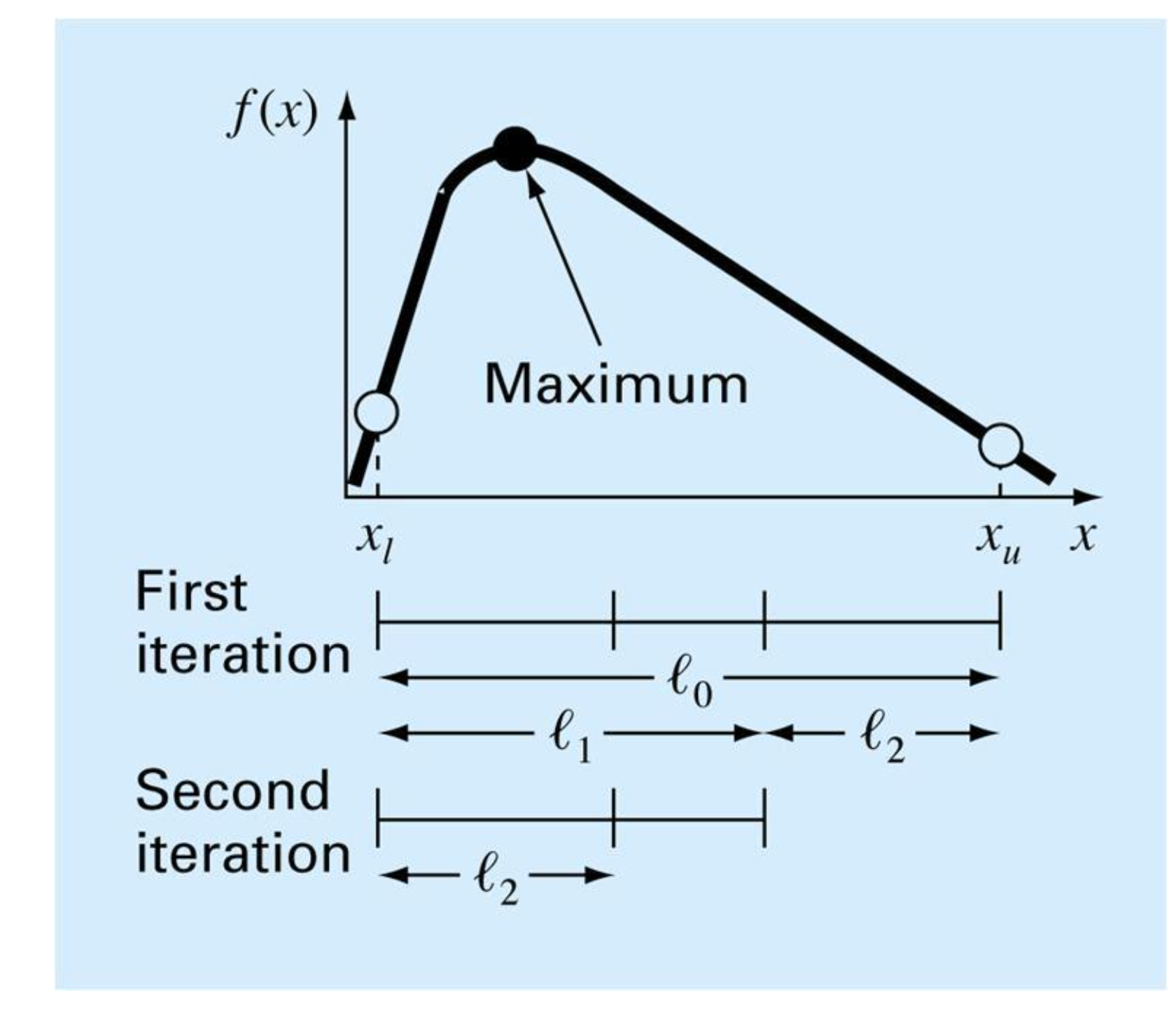
- 최대/최소값의 앞뒤에 위치하는 xl, xu 두 포인트를 고른다.
1-1. 이 두 점은 아래 속성을 만족해야 한다. - 두 점 사이에 최대값을 찾기 위해 중간에 점을 두개 고른다.
2-2. 위 두 점은 와 이며, d는 )이다.
즉, 전체 구간의 61.8% 정도가 된다.
최대값을 구할 경우
- 두 점중 함수값이 큰 점을 포함하는 세 점의 구간이 최대값을 포함할 것이므로, 함수값이 적은 점과 끝점이 포함하는 구간을 제외한다.

위 경우 x_1이 더 함수값이 크기 때문에 x_2와 x_l이 포함하는 구간을 제외한다.
최소값을 구할 경우
- 두 점중 함수값이 작은 점을 포함하는 세 점의 구간이 최소값을 포함할 것이므로, 함수값이 큰 점과 끝점이 포함하는 구간을 제외한다.

위 경우 x_2가 함수값이 더 작기 때문에 x__1과 x_u가 이루는 구간을 제외한다.
상대오차
- 상대오차가 지정한 오차보다 작아질때까지 위를 반복하게 된다.
- x_opt 는 x_1과 x_2 중 함수값이 작은/큰 것을 의미한다 ( 즉, 최대/최소값을 포함하는 구간에 있는 점의 위치 )
상대오차 =
Parabolic Interpolation
- 함수에서 세 점을 찾는다.
- 세 점을 잇는 포물선 식을 유도한다.
- 만들어진 포물선을 미분하여 0인지점 ( 최대/최소값이 있는 지점 ) 을 찾는다.
- 세 점중 3에서 찾은 점을 포함하는 두 점을 찾는다.
- 두 점과 미분값이 0이 되는 점으로 새로 2로 진행한다.
3의 값을 구하는 공식

Newton's Method
- 극대/극소 값은 1차 미분식의 값이 0이 되는 점으로도 알수 있다.
- 이 속성을 이용해, 뉴튼 렙슨 방식으로 극대/극소 값의 위치를 찾을수 있다.
Brent's Method
- Parabolic 방식을 쓰다가 안되면 Golden section 방식을 사용한다.
2차원 극대/극소 값 찾기

- 값이 가장 커지는 x와 y축의 값을 찾는다.
Random Search
- 랜덤한 (x, y) 점을 대입해 최댓값을 갱신하며 찾는다.
Univariate Pattern Search
- 한번에 한개의 변수를 바꿔가며 값이 증가하게 이동한다.
- 아래의 예시를 보면 알수 있겠지만, x값이나 y값중 하나만 변하기에 탐색이 축에 평행하게 이루어진다.

- 아래의 예시를 보면 알수 있겠지만, x값이나 y값중 하나만 변하기에 탐색이 축에 평행하게 이루어진다.
Powell's Method
- 시작점 하나와 두개의 방향을 선택한다.

- 시작점과 h1 방향을 기준으로 하여 1차원 최적화를 진행해 최대값을 찾는다.
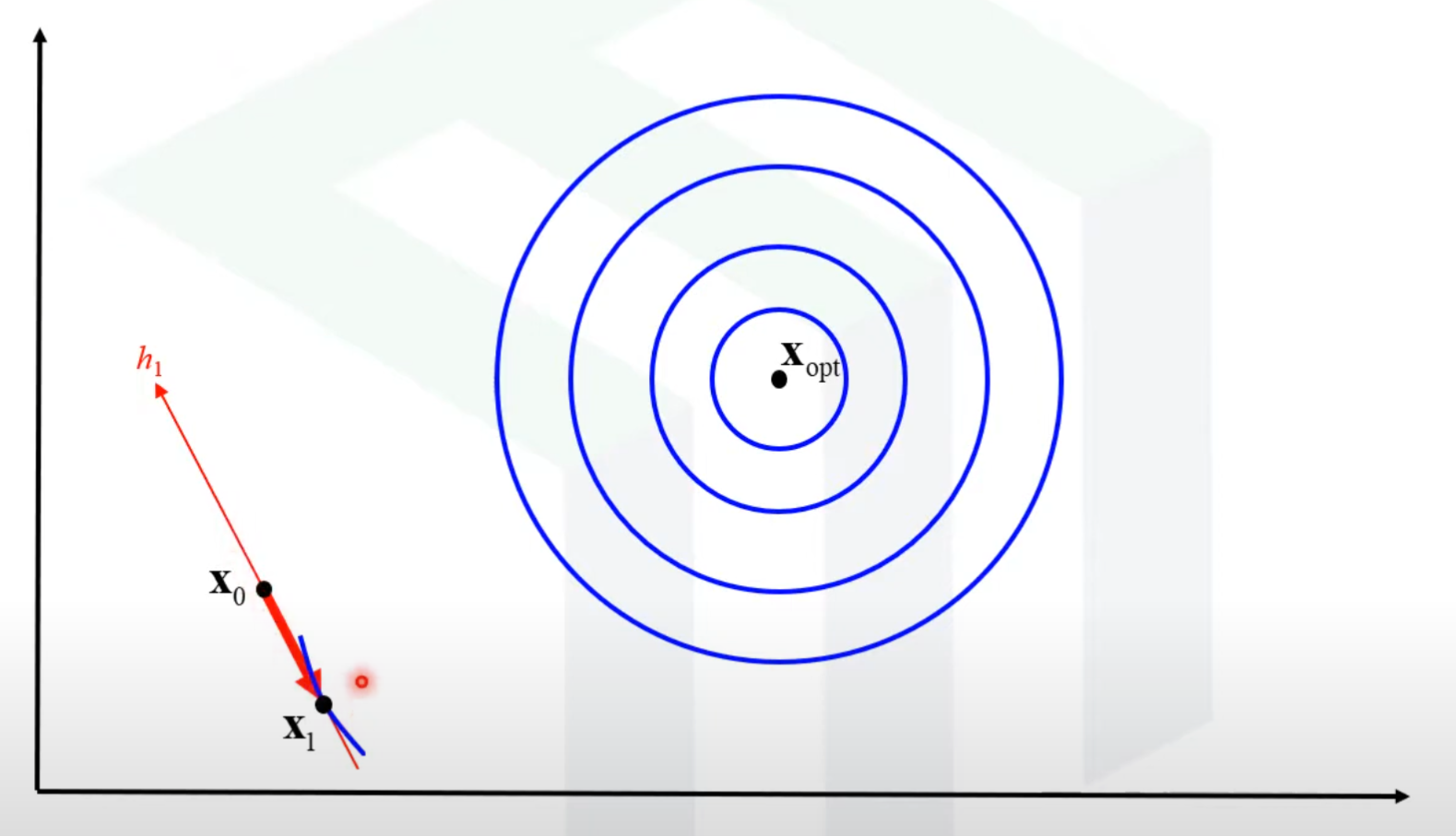
- 찾은 점과 h2 방향을 기준으로 또 1차원 최적화를 진행한다.
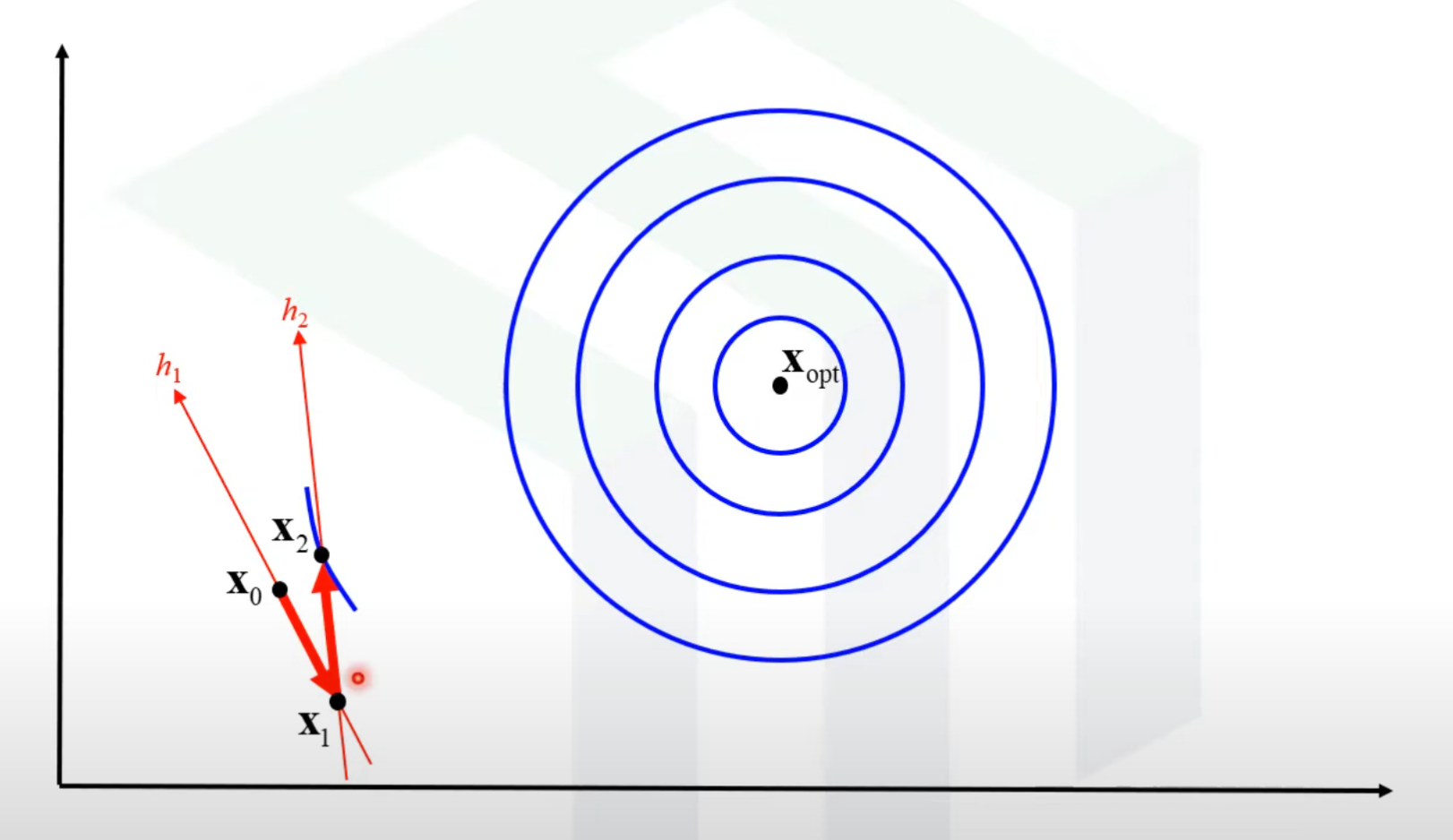
- 시작점과 3에서 찾은 최대값의 점을 잇는 방향 h3을 하나 더 찾는다.
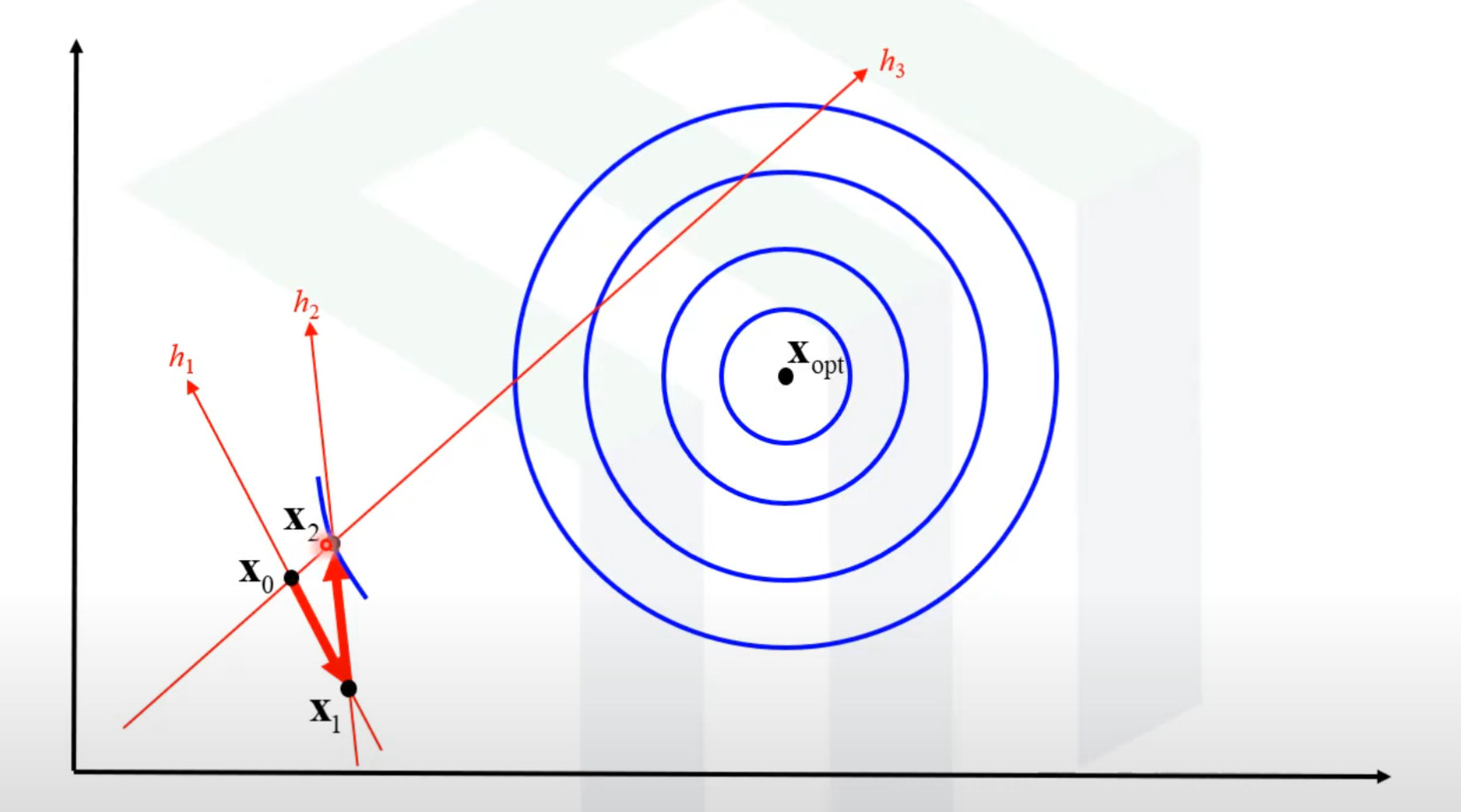
- 찾은 선을 기준으로 또 1차원 최적화를 진행해 최대값이 있는곳을 찾는다.
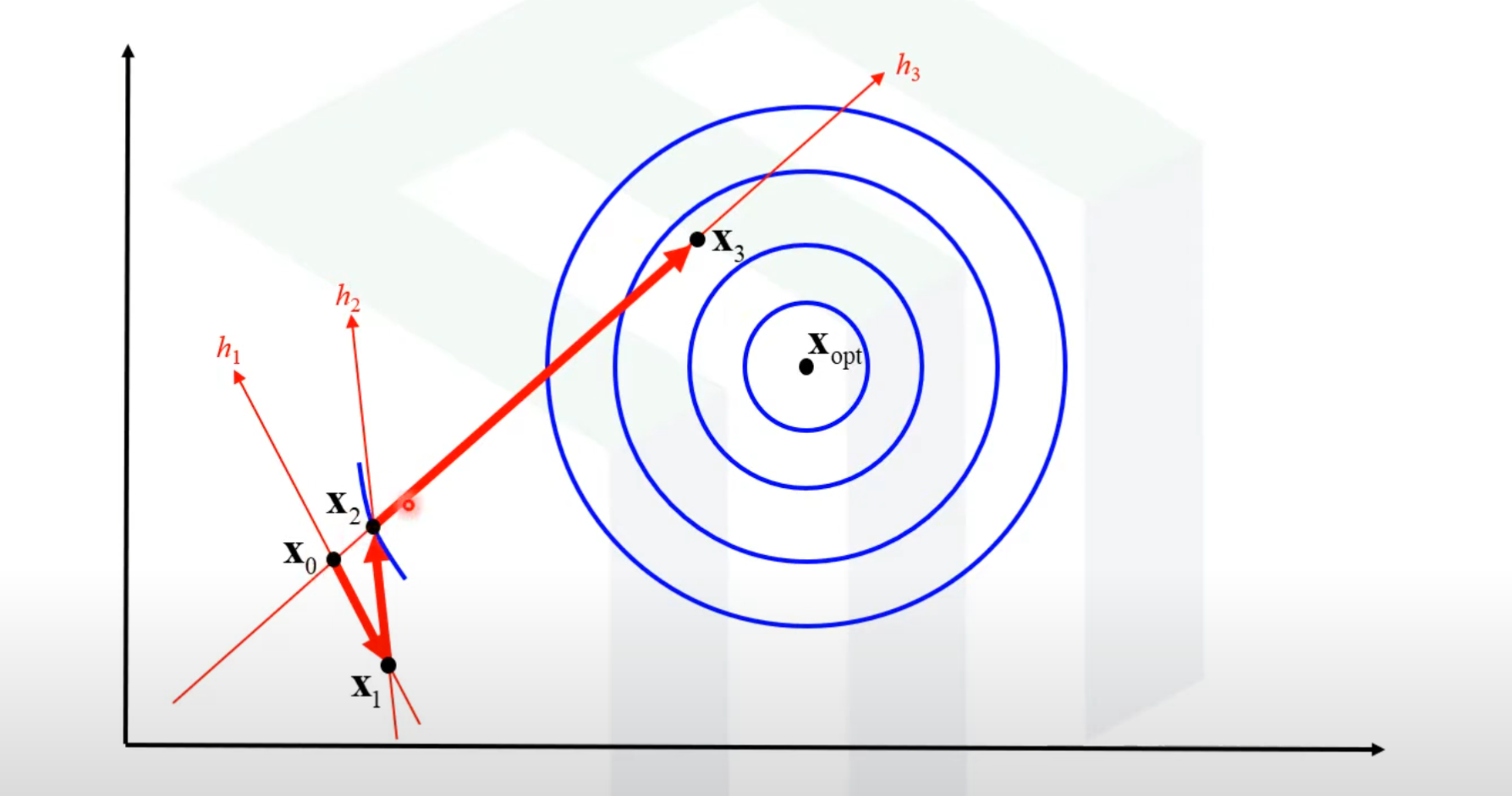
- 찾은 점에서 h2 방향을 기준으로 하여 최대값이 있는곳을 찾는다.

반복..
- 즉, 찾아놓은 최대값들의 점들을 이어 새로운 방향을 만들거나, 이전 방향을 그대로 이용해 1D 최적화를 계속 진행해 나간다.
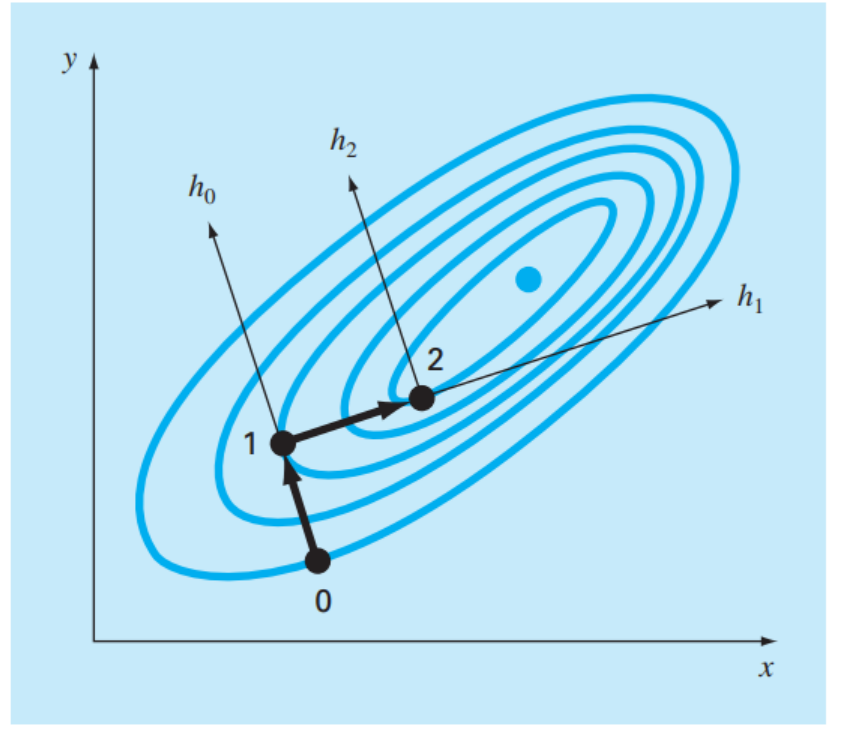
Gradient Method
- 미분을 사용한다.
- 시작점을 찾고, 그 점에서 가장 가파르게 올라가는 벡터를 찾아 그 방향으로 올라가고, 또 다른벡터를 찾아 올라가는 과정을 반복한다.
- 가파르게 올라가는 벡터는 각각 x에 대해 미분한 값과 y에 대해 미분한 값으로 이루어진다.
- 또 이는 함수의 등고선과 직각한다.
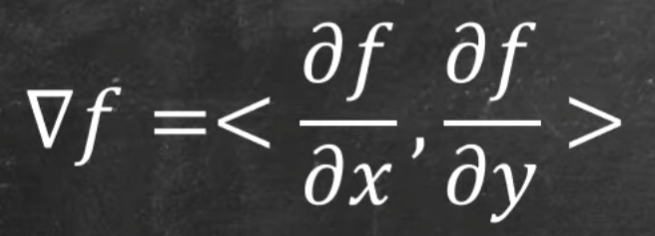
- 또 이는 함수의 등고선과 직각한다.
- 점에서 방향 * (한번에 이동할 길이) 를 더해 진행된다.
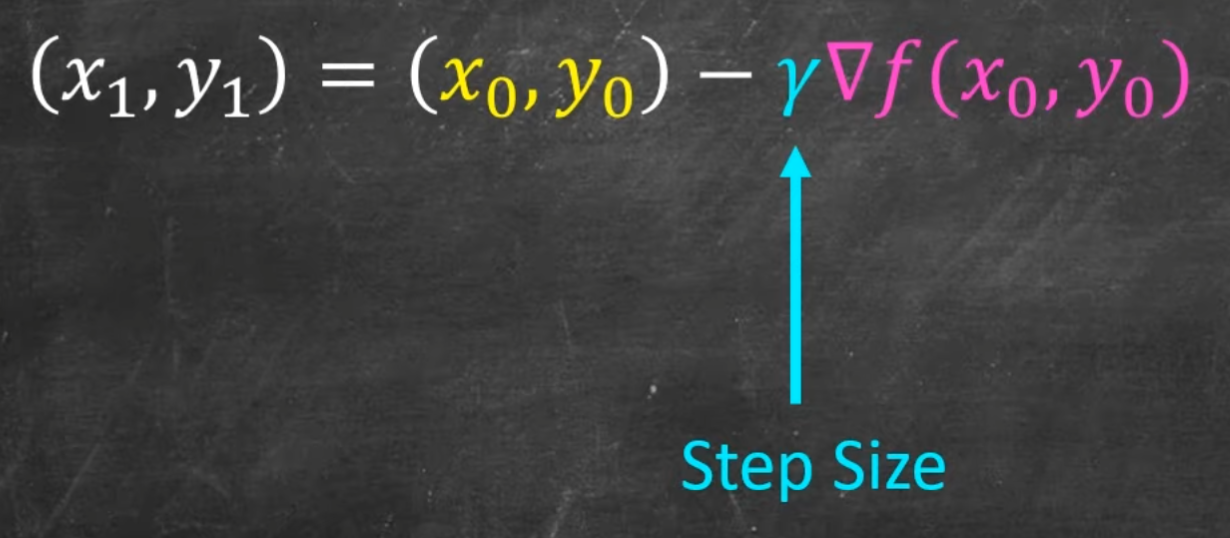
- 찾은 방향벡터 f (x, y) 를 역탄젠트에 로 하면 라디안 기준 각도를 찾을수 있다.
이동 거리
- 주어진 방향벡터로 1의 거리만큼 이동한다.

- (4, 8) f 벡터 기준 x 이동, y 이동 값 계산 예시
- atan(8/4) = 1.107
값 예측
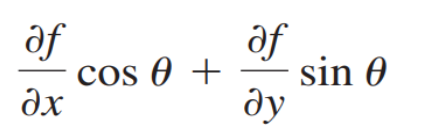
- 단위 이동 후의 결과를 위 공식으로 대략 예측 가능하다.
- x에대한 미분값 * cos + y에 대한 미분값 * sin

- 예측값과 실제값을 계산하는 예시
Hessian
- 다변수함수의 극값의 극대, 극소, Saddle을 판정한다.
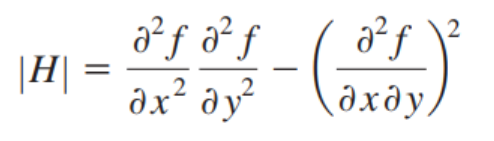
- x기준 2번미분값 * y기준 2번미분값 - ( x와 y에 대해 미분한 값 ) ^ 2
- 첫항은 2차 미분값을 의미한다!!!
- H가 0보다 크면 극대, 극소값을 가지며, x의 2차 미분값이 0보다 크면 극소값을, x의 2차 미분값이 0보다 작으면 극대값을 가진다.
- H가 0보다 작으면 Saddle point 를 가지게 된다.
Saddle
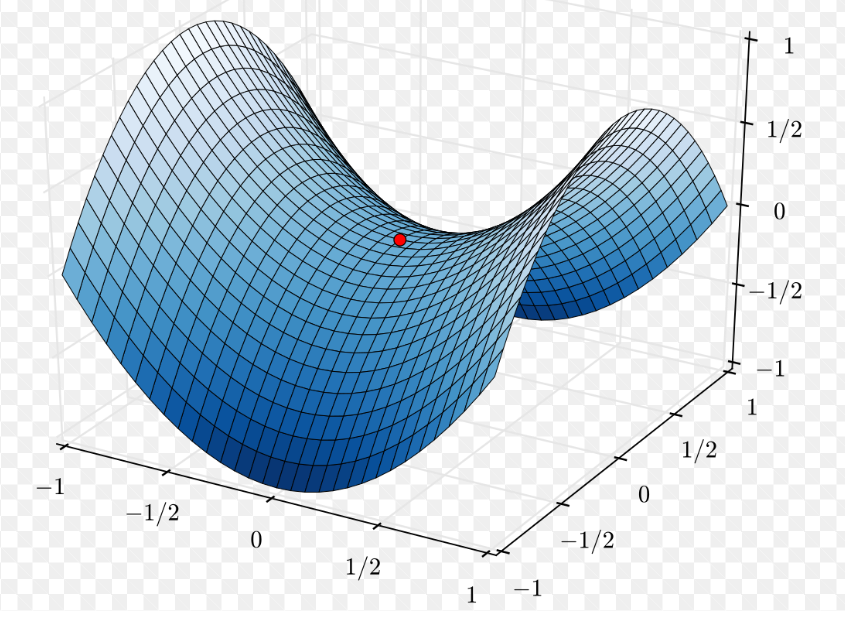
- 위 그래프에서 빨간색 점은 x로 미분했을때 최소, y로 미분했을때는 최대인 점이 된다.
- 빨간점을 Saddle point 로 부른다.
Steepest Ascent Method
- Gradient method 에서 찾은 방향벡터를 기준으로 값이 감소하기 전까지 계속 이동해 최대값에 도달하면 방향벡터를 다시 찾는다.
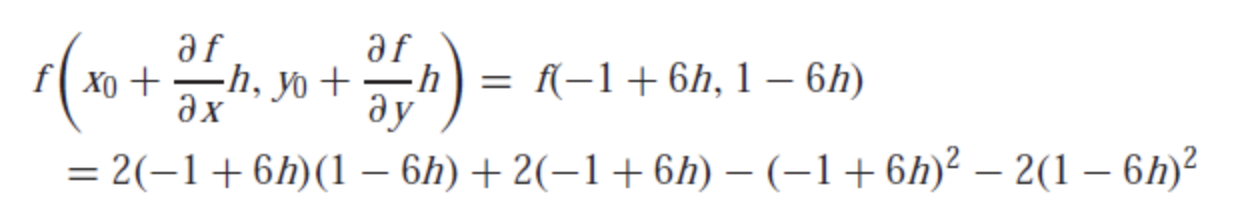
- h = 이동하는 거리
- 이동하는 거리를 기준으로, 두 변수 x, y으로 구성되었던 함수가 단일변수 함수가 되었다.
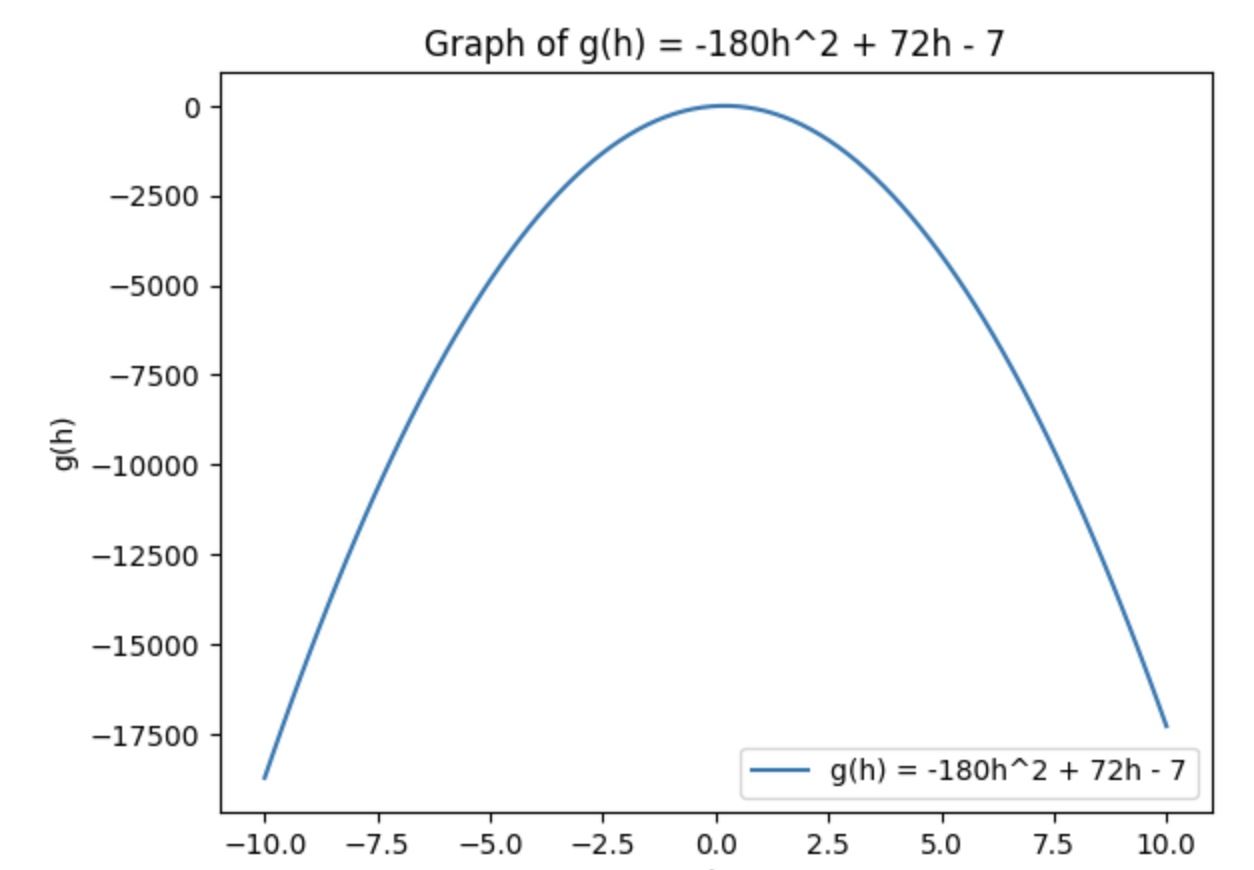
- h에 대한 그래프, 값이 최대가 되도록 하는 h의 값을 찾을수 있다.
- 여기서 찾은 h값 만큼 이동하고 다시 방향벡터를 찾아 반복한다.
라그랑주 보간법
- n+1개의 좌표로 n차 다항식을 만드는 방법
아이디어
- 특정 숫자를 대입하면 0이나 1의 값을 갖는 항을 만든다.
- (x-a)를 곱해주면 x에 a값을 대입할 때 0이 된다.
- (x-a)를 (b-a)로 나누면, x에 b를 대입했을 때 1이 된다.


뮬러법
- 방정식의 근을 찾는다.
- 세개의 점을 지나는 2차식의 근을 이용해 방정식의 근을 찾는다.
- 찾은 2차식의 두개의 근 중에서 중간 점과 가까운 근을 찾는다.

- 찾은 근을 중심으로 앞 뒤 점으로 세개의 점을 구성한다.
- 새롭게 2차식의 근을 찾아준다.
Inverse Quadratic Interpolation
- y = f(x) 가 있다.
- f(x) = 0 일때 x는 근이 된다.
- f의 역함수 g에 대해 g(0) = x가 된다.
- 즉 g(0)이 근이다!

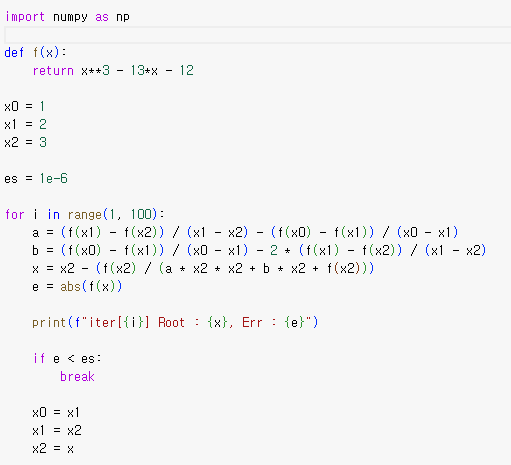
- 예시 코드
- 초기 근 x0, x1, x2를 설정합니다.
- 현재 근 x를 계산
- f(x)의 절대값을 e로 설정합니다.
- x가 근일 경우 f(x)가 0이 되어야 하기 때문이다.
- err가 허용 오차 tol보다 작으면 반복을 종료합니다.
- x0, x1, x2를 각각 x1, x2, x로 업데이트합니다.