11.21. 오전
KMOOC - 실습으로 배우는 머신러닝
중 머신러닝 프로세스 개요, 경사하강법 개요, 경사하강법 심화를 학습하였다.
머신러닝 프로세스 개요
머신러닝 프로세스
1. 도메인 지식을 기반으로 데이터를 수집하고,
2. 데이터에 대한 이해를 바탕으로 EDA 및 데이터 전처리를 진행한다.
3. 모델에 학습을 시켜 모델에 적용하고
4. 해당 모델을 검증한다.
5. 피드백을 바탕으로 모델이나 데이터 전처리 방식 등을 수정하여 원하는 성능을 얻을때까지 진행한다.
데이터 관련 용어
- Dataset : 정의된 구조로 모아져 있는 데이터 집합
- Data point(Observation) : 데이터 세트에 속해있는 하나의 관측치
- Feature(variable, attribute) : 데이터를 구성하는 하나의 특성, x
- Label(target, response) : 입력변수들에 의해 예측, 분류 되는 출력 변수, y
- 관측치의 개수 : n, feature의 개수 : p로 주로 표현한다.
분류와 회귀
- 분류(classification) : 종속변수가 범주형일 때 사용하는 방법
- 회귀(regression) : 종속변수가 연속형일 때 사용하는 방법
데이터 준비 과정
-
Dataset Exploration(EDA) : 데이터 모델링을 하기 전에 데이터 변수 별 기본적인 특성들을 탐색하고 데이터의 분포적인 특징 이해. 데이터의 의미를 잘 파악한 후 머신러닝에 활용해야 한다. 데이터를 잘 살펴보고, 이에 적절한 머신러닝 모델을 선택하는 것이 아주 중요하다!
-
Missing value : 데이터를 수집하다 보면 일부 데이터가 수집되지 않고 결측치로 남아있는 경우가 있으므로 보정이 필요하다.
-
Data types and conversion : 데이터 셋 안에 여러 종류의 데이터 타입이 있을 수 있으므로, 이를 분석이 가능한 형태로 변환 후에 사용해야한다.
-
Normalization : 데이터 변수들의 단위가 크게 다른 경우들이 있고, 이러한 것들이 모델 학습에 영향을 주는 경우가 있어서 정규화 하는 것이 필요할 수 있다.
-
Outliers : 관측치 중에서 다른 관측치와 크게 차이가 나는 관측치들이 있고 이러한 관측치들은 모델링 전 처리가 필요할 수 있다.
-
Feature selection : 많은 변수 중에서 모델링을 할 때 중요한 변수가 있고 그렇지 않은 변수가 있어서 선택이 필요한 경우가 있다. 모델의 설명 가능성에 대해 이야기할 때에도 많이 사용된다.
-
Data sampling : 모델을 검증하거나 이상 관측치를 찾는 모델링을 할 때 또는 앙상블 모델링을 할 때 가지고 있는 데이터를 일부분 추출하는 과정을 거치기도 한다. 우리 실습에서는 사이즈가 너무 큰 데이터에 대해서 전 처리 및 EDA를 할 때, 일단 샘플링한 데이터를 통해 빠르게 진행해본 뒤 전체 데이터에 대해 적용하기도 했었다.
대부분 머신러닝 과정 중 70% 시간은 데이터 준비에 들어가는 시간이다!
실제 모델에 학습을 시키고 적용하는 시간은 30% 뿐!
데이터 모델링
- 모델은 입력 변수와 출력 변수 간의 관계를 정의해줄 수 있는 추상적인 함수 구조.
- Training data 를 통해 모델을 학습하고, test data로 검증한다. 그 후 피드백을 통해 모델을 수정하거나, EDA와 전처리를 다시 해주는 등의 방법으로 원하는 성능이 나올 때까지 진행한다.
- 다양한 모델들을 사용할 수 있다.
모델링 검증
- Underfit : prediction error to training data (Loss) : 너무 간단하게 학습했다.
- Overfit : predictiona error to validation data(Generalization error) : 너무 복잡하게 학습했다.
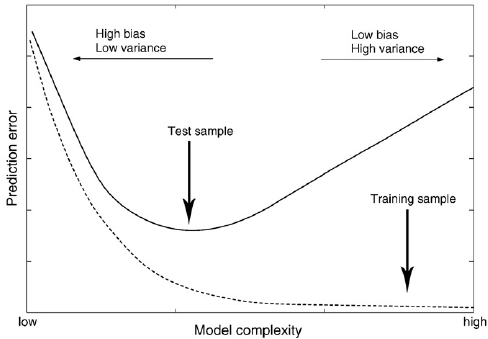
training error와 test error(validation error)간의 그래프
- test error가 최소가 되는 지점이 가장 적합한 복잡도 수준이다.
- 모델의 복잡도는 하이퍼파라미터 튜닝을 통해 조정할 수 있다.
- bias-variance trade-off에 의한 현상이다.
검증 방법
- Validation with training data only (X) : 거의 사용하지 않는다.
- Training, test data 이용 -> 하이퍼파라미터의 검증에 문제가 있다.
- Training, validation, test data 이용 -> hold out validation
- Cross validation -> 데이터의 수가 적어 hold out validation 을 진행하기 어려운 상황에서도 사용할 수 있다. 시간은 좀 오래걸리지만 검증의 정확도가 높다.
- 일반적으로는 hold out validation을 사용한다고 한다.
그동안 배운 내용들을 리마인드해보며 머신러닝의 전체 프로세스를 되짚어볼 수 있는 시간이었다.
경사하강법
어렵다!
최적화(Optimization)
- 최적화란?
loss function을 최소로 만드는 머신러닝 모델을 얻어내는 것.
경사하강법 개요
경사하강법은 Iterative algorithm-based optimization 이다.
쉽게 생각하면, loss function의 기울기(gradient)가 작아지는 방향으로 반복적으로 이동하며 최소값에 도달하는 방법이다.
필요성
- 손실 함수가 어떻게 생겼는지, 식이 무엇인지 파악할 수 없는 경우, 혹은 너무 복잡하여 미분이 불가능한 경우가 존재한다. 그럴 때 현재 알고 있는 것은 현재의 함수값, 그리고 몇가지 추가적인 정보 뿐이다. 이때 함수의 최소값을 찾기 위해 gradient - descent가 필요하다. 이를 이용하면 함수를 미분하여 최소값을 구하지 않고, 비교적 간단하게 최소값을 알아낼 수 있다.
경사하강법이란?
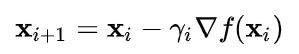
최적화할 함수 f(x)에 대해서, 현재지점을 Xi라고 했을때, 다음 지점 Xi+1은 위와 같은 수식으로 구할 수 있다.
감마는 step size 혹은 learning rate로, 이동할 거리를 조정할때 사용하는 하이퍼파라미터이다.
식에 대해 이해해보면, 현재 지점에서 그 지점의 기울기(gradient)와 step size를 곱한 값을 빼준다.
이는,
방향에 대해서는 기울기의 반대 방향으로 이동해야 최소값에 다가갈 수 있기 때문이며,
크기에 대해서는 최소값으로 다가갈수록 graident의 크기가 작아지기 때문이다.
step size
적절한 step size를 찾는 것도 중요하다.
- 만약 step size가 너무 크면?
진동하여 최적해를 찾지 못할 가능성이 있다. - 만약 step size가 너무 작으면?
최적해를 찾는 학습에 시간이 너무 오래 걸린다.
한계
경사하강법은 global minimum을 찾는 것을 보장할 수 없다.
만약 찾아가는 중간에 local minimum이 존재한다면, 거기서 멈추게 될 수 있기 때문이다.
하지만 local minimum도, 다른 지점에 비해 머신러닝의 성능이 좋게 나오는 것이 입증되었다고 한다.
또한, 너무 큰 데이터에 대해서는 시간이 너무 오래 걸린다는 단점도 존재한다.
stochastic gradient
gradient descent 방법에 시간이 너무 오래걸린다는 단점을 극복하기 위해 사용하는 방법이다.
간단히 이해하면 데이터를 여러개의 batch로 나누어 각각에 gradient descent를 적용한다고 생각할 수 있다.
극단적으로는 하나의 샘플만 사용하기도 한다. 그러나 이 경우 오히려 시간이 오래걸릴수도 있다.
위 방법들은 성능은 유지하면서도 computational cost를 줄여 빠르게 해를 구할 수 있다는 장점이 있다.
Momentum
gradient descent를 통해 local minimum이 아닌 global minimum을 찾기 위해 더해주는 값. 관성이라는 뜻이다.
시간이 없어 찾아보진 못했지만, 관성이 있어, 원하는 만큼보다 더 가게 되었을 때, 그 부분이 local minimum이라면 그 반대 쪽으로 gradient 가 작아질 거니까...
local minimum에서 벗어나 global minimum을 찾을 수 있도록 더해주는 값이라고 이해했다.
특히 saddle point(안장점)에 대해서는 잘 벗어날 수 있다는 효과가 존재한다!
오후에 경사하강법 좀 더 찾아보고 시작하자!
참고한 블로그
Momentum에 대해 되게 잘 정리해주신 분이 있어 읽어봤다!
이를 토대로 추가적으로 이해해보면, 모멘텀이란 관성을 의미한다.
즉, '이전' 기울기의 방향 및 크기를 토대로, 해당 방향으로 관성을 가져 그만큼 추가로 이동하게 해주는 것이 바로 모멘텀이다. local minimum에 빠질 수 있는 상황에서 이러한 기법을 사용하면 추가로 이동하므로 빠져나갈 수 있다. global minimum에서는 빠져나갈 수 없고!
수식에 대해서 살펴보면,
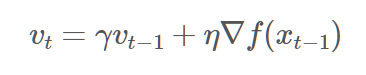
경사하강법에서 빼주는 값이 위 모멘텀으로 바뀐다.
관성계수와 그 전 모멘텀을 곱한 값에, 학습률과 그라디언트를 곱한 값을 더해준 것이 모멘텀이다.
결국 원래 빼주는 값에 관성계수 * 전 모멘텀을 더해준다.
관성계수는 보통 0.9 정도로 사용한다고 한다.