[Day 49] KNN, 로지스틱 회귀, Decision Tree

임종우·2022년 11월 21일
KNNdecision tree로지스틱 회귀
0

ai_school_TIL

목록 보기
30/34

K-MOOC 실습으로 배우는 머신러닝
11.21 두 번째 시간
이번에는 KNN, 로지스틱 회귀 등 수업에서 다루지 않았던 모델들의 개요에 대해 살펴보았고,
Decision Tree의 원리와 작동 방식에 대해 더 이해해보는 시간을 가졌다!

KNN (K-Nearest Neighbors)

classifier의 대표적인 모델
굉장히 직관적이며 간단하고, 이해하기도 쉬운데 성능도 꽤 괜찮은 알고리즘이라고 한다!
어떤 데이터가 주어지면, 그 주변의 데이터를 살펴본 뒤 더 많은 데이터가 포함되어 있는 범주로 분류한다.

컨셉

이는 관측치들 끼리의 거리가 가까우면, Y도 역시 비슷할 것이라는 가설을 기반으로 한다. 따라서 새로운 데이터가 들어왔을때, 주변 K개의 데이터의 class를 조사하여, 다수결의 원칙(majority voting)에 따라 더 많은 쪽이 속해있는 class로 해당 데이터를 분류한다.

하이퍼파라미터

K값을 하이퍼파라미터로써 바꾸어주며 모델을 조정할 수 있다.
K가 클 수록 모델의 complexity가 떨어질 것이며, K가 작을수록 complexity가 클 것이다. K가 너무 크다면 underfitting, 작으면 overfitting이 생긴다.
일반적으로 홀수를 사용한다. (짝수이면 동점이 나올 수 있으므로)

특징

기본 함수나 수식이 있는 다른 모델들과는 다르게, 이는 거리를 계산하여 적용하는 방식이다.
따라서 미리 학습을 할 필요 없이, testing 할 데이터가 들어오면 training data와의 거리를 구하고 최종 결과를 내놓는 이 모델은 lazy learning algorithm 이라고 부르기도 한다.
위와 같은 특징으로 인해 실시간적으로 큰 데이터에 대해서 사용하기는 어려울 수 있다.
최적의 K값은 validation set 등을 이용해 경험적으로 알아내야 한다. bias-variance trade off 를 고려하여 정한다.

거리 측정 공식

KNN에서 가장 중요한 것 중 하나가 바로 거리 측정 공식이다.
1. 유클리드 거리(Euclidean Distance)
우리가 일반적으로 생각하는 점과 점 사이의 거리를 구하는 공식이다.

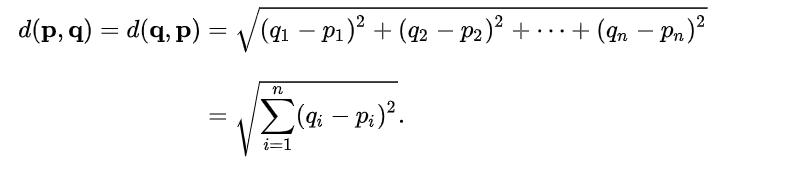
  1. 맨해튼 거리(Manhattan Distance)
    점들 사이의 직선 거리가 아닌, 각 축 별 거리를 합쳐준 거리이다.

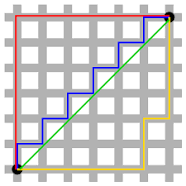
보통 유클리드 거리를 많이 사용하지만, 측정하는 대상에 대해 완벽히 독립적으로 생각하여 변수별로 거리를 계산하고자 할 때에는 맨해튼 거리를 사용한다고 한다.

scikit-learn에서

from sklearn.neighbors import KNeighborsClassifier

위와 같이 import 하여 사용할 수 있다!
공식문서
n_neighbors가 K값을 의미한다.
weights에 {‘uniform’, ‘distance’} 를 통해 거리에 따른 가중치를 줄지 말지를 결정할 수 있다.

로지스틱 회귀

로지스틱회귀란, 선형회귀 모델의 classification 버전이다!
그냥 선형회귀 모델만 사용하는 것이 아니라, 선형회귀 모델의 output을 logistic function을 이용해 변환하여 사용함으로써, 분류의 효과를 내므로 logistic regression이라고 부른다.

필요성

종속변수가 (0,1)의 값만 가지는 binary 형식일때, 회귀를 통해 이를 분석하는 것이 타당할까?
-> 선형회귀분석의 우변(회귀식)은 범위에 제한이 없지만, 좌변(종속변수)의 경우 0,1 이라는 범위의 제한이 있기 때문에 사용이 적절하지 않다.
회귀 분석을 진행할 시 엉망인 결과가 나올 것이다!

따라서, 이진 형태를 가지는 종속변수의 예측(분류 문제)에 대해 회귀식을 통해 모형을 추정하기 위해서 logistic regression이 필요하다.

분류문제임에도 불구하고 굳이 회귀식을 이용하려는 이유는?
회귀식으로 표현할 경우, 변수의 통계적 유의성 분석 및 종속변수에 미치는 영향력 등을 알아볼 수 있기 때문이다!

컨셉

  • 로지스틱 함수(sigmoid)

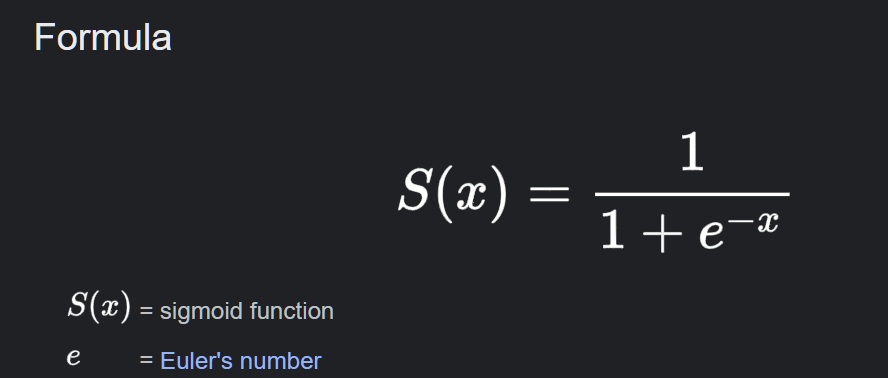
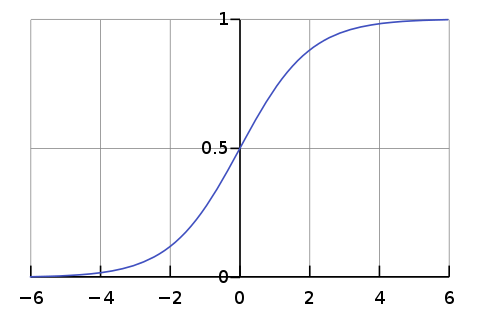
sigmoid function을 이용하면, 회귀식을 이용하면서도 종속변수의 값의 범위를 0~1 사이로 제한할 수 있다.

따라서, 회귀식으로 분류의 효과를 내기 위해, 회귀식의 결과를 sigmoid function에 넣어준다. 그렇다면 해당 식의 결과는 특정 클래스로 분류 될 확률을 의미할 것이다.

Loss 함수

logistic regression의 loss 함수로는 Cross-entrophy를 주로 이용한다.

사진 출처 : K-MOOC 강의 자료

-(실제 클래스 * 확률값에 로그를 취한 값을 모든 클래스에 더해준 값) 이다.
결국, 해당하는 클래스의 확률값에 로그를 취한 값(들을 더한 값)이 cross entrophy이다! 확률은 0에서 1 사이일거고, 거기서 값이 커질수록 로그값은 작아진다. 여기에 -가 붙어있기 때문에, cross entrophy가 작다는 것은, 확률이 1에 가까워진다는 것!

즉, loss를 minimize 해주게 되면, 실제 클래스로 분류 될 확률이 최대화된다!

강의에서는 cross - entrophy라고 배웠는데. 인터넷 찾아보다보니
Log Loss를 많이 사용한다고 한다.
참고해서 더 공부해보자!

사실, 위에서 사용한 식과 동일하다! 이건 천천히 좀 더 알아봐야겠다.....
조금 찾아봤는데, 정확하진 않지만 같은 식을 가지고 이진 분류일 경우 Log Loss function, 다중 분류에도 사용 가능한 경우 Cross-entrophy loss function이라고 하는 것 같다!

scikit-learn에서

공식문서

from sklearn.linear_model import LogisticRegression

로 사용할 수 있다!

되게 다양한 하이퍼파라미터들이 있는데.. 뭔지 잘 모르겠다.... 천천히 찾아보자!
.decision_function() method를 사용하면, 양성 클래스에 대한 z값을 반환한다.
predict_proba등을 이용해 확률을 얻을 경우, 클래스 명은 알파벳 순으로 자동 정렬된다.
선형회귀인 만큼 .coef_[]를 통해 해당 위치의 계수를 볼 수 있으며, .intercept_를 통해 y 절편값 역시 확인할 수 있다.

이진분류의 경우 시그모이드 함수를 사용해 z값을 변환하지만,
다중 분류의 경우 softmax 함수를 사용하여 z값을 확률로 변환한다.
이때, softmax 함수란 여러개의 선형 방정식의 출력값을 0~1 사이로 압축하고 전체 합이 1이 되도록 만들어진 함수라고 한다. 이를 위해서 지수함수를 사용한다. 참고
시그모이드가 1 / 1 + e^(-z)였다면, 소프트맥스는 e^(z1) / (e^(z1) + e^(z2) + ... + e^(zn))이다.
나중에 딥러닝을 배울때 나온다고 하니! 알아두자!

추가로, KNN에서 predict_proba를 이용하면 로지스틱 회귀를 이용한 것과 마찬가지로 각 클래스로 분류될 확률을 구할 수 있다.

Decision Tree

Decision Tree는 그동안 수업시간에 많이 다루었지만, 뭔가 정확한 작동원리를 파악하고 있지 못하는 느낌이었다!
이번 수업을 들으면서, Decision Tree와 Decision tree regression의 좀 더 자세한 작동 원리와, 데이터 공간 측면에서의 이해를 할 수 있었다.

Decision tree란?

분류와 회귀 작업 및 다중출력 작업도 가능한 다재다능한 머신러닝 방법론
IF_THEN 룰에 기반해 진행하여, 해석력이 아주 좋다!
CART(Classificatio and Regression tree) 알고리즘으로, 분류와 회귀 모두에 사용할 수 있다.

학습 과정

분기마다 변수와 기준을 세워 클래스들을 분류해나가는 과정을 통해 학습을 진행한다.
한번에 한 개의 변수를 사용하여 정확한 예측이 가능한 규칙들의 집합을 생성한다고 볼 수 있다.
IF then 형식으로 표현되는 규칙이 만들어진다.
예를 들어,
내일 날씨가 맑고, 습도가 70% 이하이면 아이는 밖에 나가서 놀 것이다.
내일 비가 오고 바람이 불면 아이는 밖에 나가 놀지 않을 것이다. 와 같은 규칙을 토대로 분류가 이루어질 수 있다.
이와 같은 학습 방법으로 인해 Decision tree 모델은 해석력이 우수하다고 할 수 있다.

데이터 공간 측면

Decision Tree에서, 데이터 공간 측면으로 보면 수직 분할이 이루어진다.

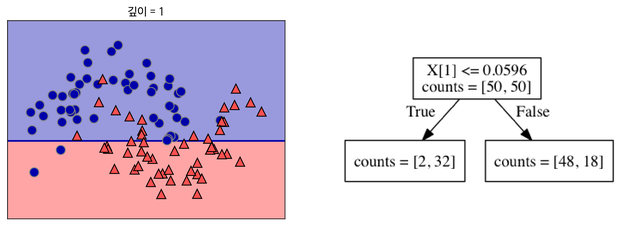
이렇게!

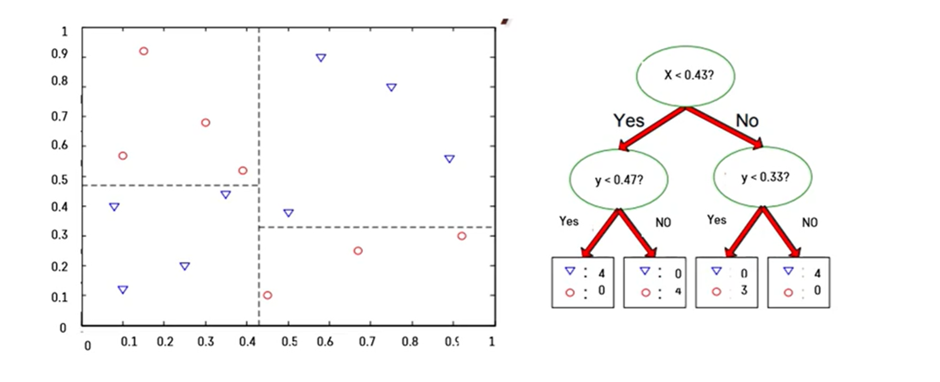
분할의 방법

데이터 공간의 순도가 증가되게끔 영역을 구분하는 방법이 바로 잘 분할하는 방법이다.
실제로는 어떻게 찾지? 불순도가 높은 영역을 찾아 관측치들 사이에서 후보군들로 경계선을 만들어 본다. 그 중에서 가장 순도를 높여주는 영역을 찾아 그어주면 된다.
데이터 공간 측면에선, 가로로도 세로로도 구분할 수 있다. 즉, 각 변수마다 구분할 수 있다.
따라서 각 변수마다 구분할 수 있는 영역을 찾아 구분해본 뒤 순도가 높게 잘 구분되는 것을 찾아 구분한다.
저렇게 분류에 대한 학습을 한 후!
새로운 test data가 들어왓을 때 해당하는 구역의 class로 분류해준다.

불순도

  • 한 노드에 속하는 샘플들의 클래스 비율을 이용해 특정 노드가 얼마나 잘 구분되었는지 측정하는 지표

  • 지니 계수
    1 - (음성 클래스 확률^2 + 양성 클래스 확률^2)
    다중 분류일 경우에도 동일하다.
    노드에 하나의 클래스만 있다면 지니 불순도는 0이 되므로 가장 작다.
    만약 클래스가 무한히 많고, 각각의 확률이 같다면 불순도가 1에 가까워질 수도 있다!

  • entropy
    지니 계수 말고 결정트리에서 불순도가 될 수 있는 값. 정보 엔트로피 혹은 섀넌 엔트로피로 배웠었다!

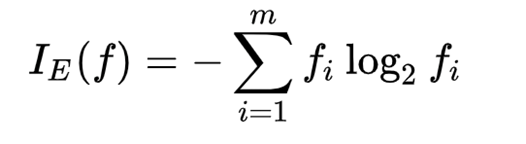
    데이터에 포함되어 있을 것으로 기대되는 평균 정보량을 의미했었다. 결국 불확실성이며 불순도이다.

  • 정보 이득
    부모 노드와 자식 노드 사이의 불순도 차이. 결정 트리 알고리즘은 정보 이득이 최대가 되도록 데이터를 나눈다.

CART 알고리즘

CART란 Classification and Regression Tree를 의미했었다.
이는 불순도를 최소화하도록 최종 노드를 계속 이진 분할하는 방법론을 의미한다.
최대 깊이가 되거나, 불순도를 줄이는 분할을 더 이상 찾을 수 없을때까지 트리를 계속 분할한다.

CART 알고리즘의 지니계수와 관련된 식이 존재한다.

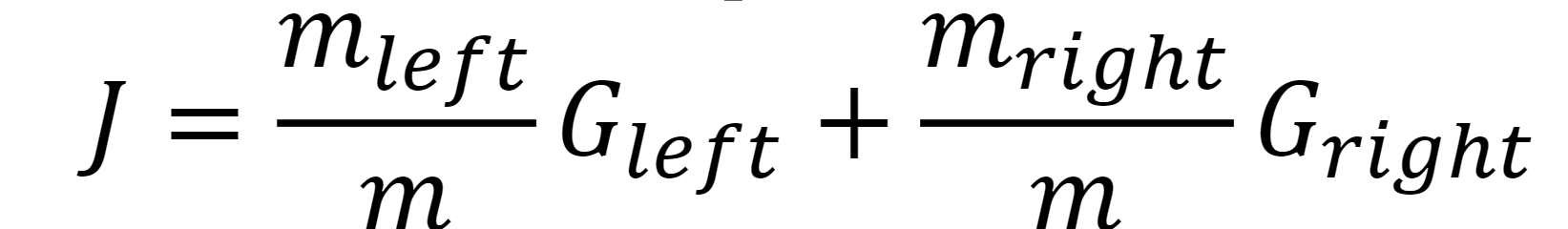
m은 각각의 서브셋으로 나누어진 샘플의 수를 의미한다.

Regularization

  • Decision Tree 모델은, 훈련 데이터에 대한 제약 사항이 존재하지 않아 과대 적합이 일어나기 쉽다. 리프노드에 속한 데이터의 개수가 하나라면 이건 지나친 일반화가 일어났다고 볼 수 있을 것이다.
  • 따라서 훈련에 제약을 둠으로써(regularization) 과대적합을 방지할 수 있다.
  • 그렇기 위해서 사용하는 파라미터들이 존재한다.
    max_depth : 트리의 최대 깊이
    min_samples_split : 분할되기 위해 노드가 가져야하는 최소 샘플 수
    min_samples_leaf : 리프 노드가 가지고 있어야 할 최소 샘플 수
    max_leaf_nodes : 리프 노드의 최대 수
    등이 존재한다.

Decision tree regression

여태까지 살펴본 내용은 분류의 경우 Decision Tree가 어떻게 동작하는지와 관련된 내용이었다.
CART 알고리즘인 만큼 회귀에도 동작할텐데, 어떤 방법으로 동작할까?
나머진 다 동일하지만, target Y 값을 처리하는데에만 차이가 있다.

분류의 경우, 나눠진 노드에 속한 관측값들의 클래스가 바로 분류의 결과가 되는 반면,
회귀의 경우, 나눠진 노드에 속한 관측값들의 타겟값의 평균이 바로 회귀의 결과이다.

분할할때 사용하는 불순도의 경우 MSE를 사용한다.
특이한 점이 있다면, 예측값이 상수라는 점이다!
MSE를 구할때 예측값은 평균인 상수이고, 노드에 속한 관측값들을 빼 제곱한 평균을 구하면 되었다.

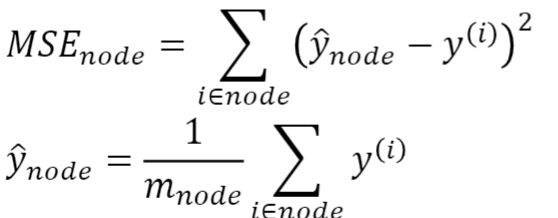
이 역시도 결정트리인 만큼 regularization을 잘 적용해주어야 한다!

참고 자료

profile
임종우
ai school 기간 동안의 TIL!
이전 포스트

[Day 49] 머신러닝 프로세스, 경사하강법

다음 포스트

[Day 50] Ensemble

0개의 댓글