[Day 40, 41] feature engineering

임종우·2022년 11월 13일

Feature Engineering log tranform

ai_school_TIL

목록 보기

27/34

22.11.08. ~ 22.11.09.
피쳐 엔지니어링에 대해 배웠다.
상당히 다양한 피쳐 엔지니어링 방법이 존재한다.
잘 익혀두고 적재적소에 활용하면 좋겠다!

내용들은 멋쟁이사자처럼 AI SCHOOL 7기 박조은강사님(오늘코드)의 자료를 참고하였습니다.

데이터 분석의 과정

데이터 분석에 정해진 과정과 순서는 없다. 그러나 대부분의 경우
데이터 수집 -> 데이터 전처리 -> 탐색적 데이터 분석(EDA) -> 피쳐 엔지니어링 -> 머신러닝 모델에 적용
의 과정을 거친다.

위 과정들은 서로 엄밀하게 구분된 영역도 아니며, 진행하다보면 얼마든지 순서가 뒤바뀌어 일어날 수 있는 과정이다.

그러나 내가 지금 하고 있는 일을 체계화하여 살펴보기 위해 해당 과정들을 나누어 진행해보면 좋다.

머신러닝의 전반적인 과정들을 살짝 체험했으니, 이 날부터는 피쳐 엔지니어링에 대해 공부해보았다.

feature engineering

데이터에 대한 지식을 바탕으로 feature를 생성, 변경, 삭제하는 등의 조작을 통하여 사용하기 더 유용한 형태로 바꾸는 것.
데이터의 전처리와 EDA를 통해 피쳐에 대한 기본적인 탐색을 진행한 후, 이를 토대로 진행한다.

피쳐엔지니어링을 위한 EDA를 진행할 때 파악해야할 사항 몇가지를 살펴보자면,

피쳐엔지니어링을 진행할 때에는 특히 피쳐의 자료형(수치형, 범주형)이 중요하다. 자료형을 보는 방법은

df.info()
df.select_dtypes(include = np.number)
df.select_dtypes(include = 'object')

위 방법들이 존재한다.

결측치 탐색 역시 중요하다. 결측치는 nan으로 들어가있을 수도 있으나, 공백, '-', 0 등 다양한 형태로 포함되어있을 수 있다. 따라서 자료의 도수분포를 살펴보거나 히스토그램을 살펴보는 등 다양한 방법으로 결측치를 탐색할 필요가 있다.
이상치를 탐색하고 판단하는 것 역시 중요하다. IQR등을 이용해 값의 범위에 따라 이상치를 찾을 수도 있고, 시각화를 통해 그래프를 이용하여 찾을 수도 있다. 이상치는 데이터의 해석과 모델의 학습을 방해하므로 제거하거나 대체해주는 것이 필요하다.
희소값에 대한 처리 역시 필요하다. 범주형 변수에 대해 희소값이 존재하는 경우, 이는 데이터의 경향을 파악하기 어렵게 만들어 해석을 어렵게하고 머신러닝의 성능을 낮출 수 있다. 인코딩을 진행할 때에도 오랜 계산시간과 많은 컴퓨팅 성능을 요구하기도 한다. 따라서 희소값들의 경우 '기타'와 같이 묶어주거나, 결측치 처리해주기도 한다.

그럼 피쳐 엔지니어링에 대해 하나씩 살펴보자.

Feature selelction (특성 선택)

해당 분야의 전문 지식, 피쳐의 중요도 등에 따라 사용할 피쳐를 선택하는 것.
중요하지 않은 피쳐가 머신러닝의 성능에 악영향을 미치는 것을 방지하기 위해 사용한다.
EDA를 통해 이를 선택하는 것도 중요하지만, 직접 모델에 추가하고 제거해보면서 검증해보는 방법도 필요하다.

Feature extraction (특성 추출)

피쳐들의 조합으로 새로운 피쳐를 생성하는 것.
PCA(주성분 분석)과 같은 기법이 이에 해당한다고 한다.
피쳐들을 통해 새로운 특성(피쳐)을 추출해본다고 생각할 수 있다.

Transform (변형, 파생변수 만들기)

기존의 존재하는 변수의 성질을 이용해 새로운 변수를 생성하는 것
새로운 피쳐를 생성하는 것이 특징을 더 잘 드러내는 경우가 존재한다.
반면, 파생변수를 만들어 사용하였을때 머신러닝 모델의 성능이 오히려 떨어지는 경우도 많다.

Polynomial Expansion(power transform)

주어진 다항식의 차수 값에 기반하여 파생변수를 생성하는 방법
예를 들어, [a,b]에 대해 최대 차수가 2차수로 주어지면 1, a, b, aa, ab, bb를 만든다.
머신러닝 모델은 label에 대해서 설명력이 높은 한두가지 feature에 기반할때보다 여러가지 feature에 기반할 때 성능이 더 뛰어나기 때문에 ‘변수를 뻥튀기 시켜준다’라는 측면에서 유용할때가 있다. 소수의 feature에 기반하게 되면 과대적합이 일어날 확률이 높아지므로!
Uniform 한 값은 어딘가는 많고 어딘가는 적은 그런 특징이 없기에, 구분되는 특징이 부족할 수 있는데, power transform 등을 통해 값을 제곱을 해주거나 하면 특징이 더 구분되어 보일 수 있다!
scikit-learn에서

# preprocessing - PolynomialFeatures
from sklearn.preprocessing import PolynomialFeatures

poly = PolynomialFeatures(degree = 2)
house_poly = poly.fit_transform(train[['MSSubClass', 'LotArea']])

pd.DataFrame(house_poly, columns = poly.get_feature_names_out())
>>>
	1	MSSubClass	LotArea	MSSubClass^2	MSSubClass LotArea	LotArea^2
0	1.00	60.00	8,450.00	3,600.00	507,000.00	71,402,500.00
1	1.00	20.00	9,600.00	400.00	192,000.00	92,160,000.00
2	1.00	60.00	11,250.00	3,600.00	675,000.00	126,562,500.00
3	1.00	70.00	9,550.00	4,900.00	668,500.00	91,202,500.00
4	1.00	60.00	14,260.00	3,600.00	855,600.00	203,347,600.00
...	...	...	...	...	...	..

Scaling (범위 변환)

범수의 분포가 편향되어 있을 경우나 이상치가 많이 존재하는 경우 등, 변수를 활용하기 어려울 때 변수의 범위를 변환해주는 것
여러 피쳐들의 범위가 서로 다를때엔 피쳐끼리의 비교가 어렵고, 모델에 학습시킬때에 중요도가 다르게 판단될 수도 있다. 스케일링은 이러한 문제를 해결할 수 있다.
피쳐 스케일링이 잘 되어 있다면, 머신러닝 모델의 성능은 상승하며, 경사하강법, KNN, clustering과 같은 거리 기반 알고리즘에서 더 빨리 작동한다.
일부 스케일링의 경우 이상치의 영향을 줄여주기도 한다.
그런데, 트리 기반 모델의 경우(결정트리, 랜덤포레스트) 데이터의 절대적인 크기보다 상대적인 크기가 중요하게 작용하기 때문에 피쳐 스케일링이 따로 필요하지 않다.

Standardization, Normalization (Z-score)

평균을 0으로, 표준편차를 1로 만들어주는 스케일링 기법
(X - X.mean()) / X.std()
변수가 왜곡된 분포를 가지고 있거나, 이상치를 가지고 있다면 예측력을 손상시킬 수 있다는 단점이 있다.

사이킷 런에서 사용하기
feature engineering에서 사용할 대부분의 사이킷런 기능들은 sklearn.preprocessing에 존재한다.
또한, 대부분 fit을 한 후 transform 을 진행하는 방식으로 사용하며, fit은 분포나 기술통계값을 파악하는 등의 역할, transform은 계산을 통해 실제 피쳐엔지니어링을 진행해주는 역할을 한다.
대부분 인자에 Series가 아닌 DataFrame 형을 요구한다.
그리고 이때 주의할 점은, fit은 train set에 대해서만 진행한다는 점이다! test set에는 fit 시키지 않고 transform 만 진행한다.

from sklearn.preprocessin import StandardScaler

ss = StandardScaler()
ss.fit(train[[feature]]).transform(train[[feature]])

# 또는
# ss.fit_transform(train[[feature]])

Min-Max Scaling

변수의 최솟값을 0으로, 최댓값을 1로 만들어 주는 스케일링 기법
(X - X.min()) / (X.max() - X.min())
표준화와 마찬가지로, 왜곡된 분포 혹은 이상치가 있는 변수의 예측력을 손상시킬 수 있다.

from sklearn.preprocessing import MinMaxScaler

ms = MinMaxScaler()
train[['SalePrice_mm']] = ms.fit(train[['SalePrice']]).transform(train[['SalePrice']])

Robust Scaling

표준화와 유사한 방식이지만, 평균이 아닌 중간값과 표준편차가 아닌 IQR에 따라 분포를 조정해준다.
중간값을 빼주고 IQR 값으로 나눠준다. -> 중간값이 0이 된다.
(X - X.median()) / (IQR)
IQR은 3분위수 - 1분위수를 의미한다.
해당 스케일링 방법은, 평균이 아닌 중간값을 사용하므로, 이상치에 강건하다는 장점이 존재한다!

from sklearn.preprocessing import RobustScaler

rs = RobustScaler()
train[['SalePrice_rs']] = rs.fit_transform(train[['SalePrice']])

사이킷런으로 위 스케일링들을 진행한 경우, .inverse_transform을 통해 원래 값으로 복원할 수 있다.

위 세가지의 스케일링을 진행하여도, 변수의 분포 형태는 변하지 않는다.

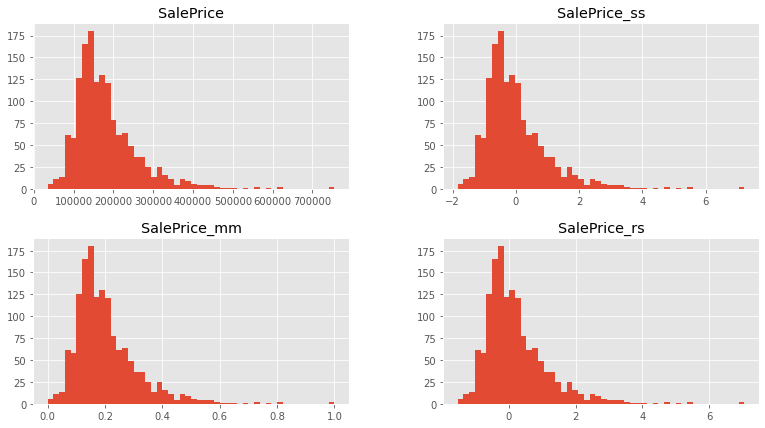
위 그림은 원래 변수, Standard Scaling 해준 변수, minmax scaling 해준 변수, robust scaling 해준 변수의 histogram을 나타낸 것이다. 값의 크기에 차이는 있지만, 스케일링을 진행해주어도 변수가 가지고 있는 확률 분포는 달라지지 않음을 알 수 있다.

확률 분포를 달라지게 하기 위해서는, log transform 을 진행해야 한다.

log transform

변수에 로그를 씌워줌으로써 분포를 변경하는 방법
로그를 씌워주면, 왜곡되고 치우쳐져 있는 분포가 좀 더 고르게 정규분포에 가까워지는 효과가 있다. (로그함수의 그래프를 보면, x 값이 클수록 기울기가 작아진다. 즉, 로그를 씌우면 작은 x에 대한 변화는 더욱 커지고, 큰 x에 대한 변화는 작아지는 효과가 있다.)
변수의 분포가 고르게 될 수록, 예측력은 상승한다고 할 수 있다.
대부분의 예측은 확률적으로 분포의 중앙 근처에서 일어날 것이기 때문! 변수의 분포가 왼쪽으로 치우쳐져있다면, 가운데 부분은 많이 학습되지 않은 상태일거고, 따라서 모델의 예측력은 하락한다 생각할 수 있다.

0602 실습에서!

실습에서, log1p를 통해 label 변수를 log transform 하고, 모델 학습 및 예측을 진행하였다. 그리고 그 예측값을 expm1으로 원래 분포의 값으로 변환시켜 최종 예측값을 구했다.
log1p란 1을 더한 후 로그를 취해준 값(로그를 취한 값이 음의 무한대로 가는 것을 방지), expm1은 지수함수를 취한 후 1을 빼주는 것을 의미한다.
log transform을 진행한 후 standardization을 한다면, 변수의 분포를 표준정규분포에 가깝게 만들어줄 수 있다.

Binning (범주화)

수치형 변수를 범주형 변수로 변환하여 주는 것
즉, 수치형 변수를 일정 기준으로 나누어 그룹화 해준다고 할 수 있다.
이를 잘 활용한다면 유사한 예측 강도를 가진 속성들을 그룹화하여 모델의 성능을 개선하는데 도움이 될 수 있다. 또한 수치형 변수의 과대적합을 방지할 수 있다.

equal width binning (cut)

수치형 변수를 동일한 길이의 N개의 bins로 나눈다.
예시로는 절대평가, 히스토그램 등이 있다.
편향된 분포에 대해 민감하다는 단점이 있다.

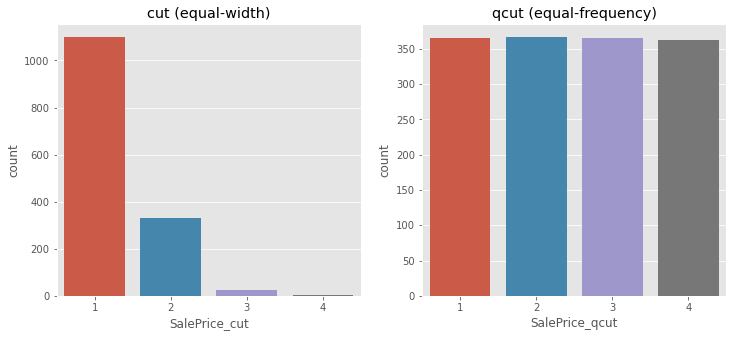
pd.cut(train['SalePrice'], bins = 4, labels = [1,2,3,4])

pd.cut의 인자로는 구간을 나누어줄 개수인 bins가 들어간다.

equal frequency binning (qcut)

수치형 변수를 동일한 관측값의 수를 가지는 N개의 bins로 나눈다.
예시로는 상대평가가 있다.
알고리즘의 성능을 높이는 데 도움이 될 수 있으나, 오히려 방해가 될 수도 있다.

pd.qcut(train['SalePrice'], q=4, labels = [1,2,3,4])

pd.qcut의 인자로는 구간을 나누어줄 개수인 q가 들어간다.

Dummy (숫자화, encoding)

범주형 변수를 수치형 변수로 변환해주는 것
데이터 시각화 또는 머신러닝 모델을 사용할때 범주형 변수를 사용하지 못하는 경우가 존재한다. 이럴때에는 인코딩을 해주어야 한다.

Ordinal Encoding

범주형 변수의 고유값들을 임의의 숫자로 바꿔준다.
이때 기본적으로는 0부터 1씩 증가하는 정수로 지정한다.
이러한 표현방식으로 인해, 그 값이 크고 작음이 있는 순서형 변수일 경우 괜찮지만, 그렇지 않은 명목형 변수에 대해서는 오해를 불러일으킬 수 있다.
pandas에서는 category형 변수의 .cat.codes로 사용할 수 있다.

train['MSZoning'].astype('category').cat.codes

scikit-learn에서는

# preprocessing - ordinal encoder
from sklearn.preprocessing import OrdinalEncoder

oe = OrdinalEncoder()
train[['MSZoning_ohe']] = oe.fit_transform(train[['MSZoning']])
display(train[['MSZoning','MSZoning_ohe']].sample(6))
oe.categories_

ordinal encoder를 선언한 후, fit시키고 transform 시켜주면 된다.
역시 주의할 점은 인자로 DataFrame 형태를 주어야한다는 점.
그리고 fit은 train set에만 진행하고 train은 transform 만 진행해야한다는 점.

공식문서 예시는 이렇다.

from sklearn.preprocessing import OrdinalEncoder
enc = OrdinalEncoder()
X = [['male', 'from US', 'uses Safari'], 
     ['female', 'from Europe', 'uses Firefox']]
enc.fit(X)
print(enc.transform([['female', 'from US', 'uses Safari']]))
print(enc.categories_)
>>>
[[0. 1. 1.]]
[array(['female', 'male'], dtype=object), array(['from Europe', 'from US'], dtype=object), array(['uses Firefox', 'uses Safari'], dtype=object)]

One-Hot Encoding

범주형 변수의 고유값들을 모두 하나의 피쳐로 만든 후, 그 값일 bool(0 또는 1)로 표현한다.
피쳐의 모든 정보를 유지한다는 장점이 있으나, 너무 많은 고유값이 있으면 너무 많은 피쳐를 만들어 계산이 오래걸리고, 컴퓨팅 자원이 많이 필요하다.
pandas에서는 pd.get_dummies()를 사용한다.

pd.get_dummies(train['MSZoning'])

scikit-learn에서는

# preprocessing - OneHotEncoder
from sklearn.preprocessing import OneHotEncoder

ohe = OneHotEncoder()
ohe_out = ohe.fit_transform(train[['MSZoning']]).toarray()
display(pd.DataFrame(ohe_out, columns = ohe.get_feature_names_out()).head())
ohe.categories_

OneHotEncoder는 좀 복잡하다. 차근차근히 살펴보면,
먼저 OneHotEncoder를 호출 및 선언 해주었고, fit_transform 해주었다.
이때 중요한 점은 ohe를 통해 transform 한 결과는 DataFrame이 아니라 scipy의 matrix 객체라는 것이다. 따라서 결과를 확인하기 위해서는 .toarray()를 해주어야 한다.
또한, 우리가 원하는 데이터프레임 형식으로 보기 위해서는 transform 결과 만들어진 피쳐들의 리스트를 컬럼으로 주어야 하는데, 이는 ohe.get_feature_names_out()으로 가져올 수 있다.