[Day 39] Kaggle - bike sharing (1)

임종우·2022년 11월 7일
RMSLEkaggle회귀 평가지표
0

ai_school_TIL

목록 보기
26/34

22.11.07.
먼저 kaggle titanic 데이터를 GridSearch와 RandomizedSearch까지 마무리 했다.
그 후, bike sharing 데이터를 통해 회귀 예측을 해보기 위한 과정을 시작했다.

Cross validation

  • GridsearchCV
    지정된 조합만 보기 때문에 해당 그리드를 벗어나는 곳에 좋은 성능을 내는 하이퍼파라미터가 있다면 찾지 못하는 단점이 있다.
  • RandomizedSearchCV
    랜덤한 값을 넣고 하이퍼파라미터를 찾습니다. 처음에는 범위를 넓게 잡고 그 중 좋은 성능을 내는 쪽으로 범위를 좁혀가며 사용. 조합이 최적의 조합이라는 보장이 없다는 단점이 있다.
    n_iter만큼의 estimators * cv만큼의 fold 학습

  • 결과 attribute
    Bestestimator : 어떤 분류기가 가장 좋은 성능을 내는지 알려준다.
    Bestscore : 가장 좋은 성능을 낸 점수를 알려준다.
    Cvresults : (cross validation의) 전체 report를 출력해준다. 어떤 조각이 어떤 성능을 냈는지를 알려준다.

  • hold-out validation과의 차이
    hold-out validation? 하나의 test-set을 만들어 검증하는 것. 평상시에 하듯 데이터를 train set과 test set으로 나누는 것!
    hold-out-validation 은 한번만 나눠서 학습하고 검증하기 때문에 빠르다는 장점이 있다. 하지만 신뢰가 떨어진다는 단점이 있다. hold-out-validation 은 당장 비즈니스에 적용해야 하는 문제에 빠르게 검증해보고 적용해 보기에 좋다고 한다!

EDA

  • Kaggle에서 데이터를 다운받고, 데이터를 EDA하는 과정을 거쳤다.
  • 데이터 설명을 잘 읽어보며 어떤 컬럼이 있고, 어떤 형태이며 어떤 의미를 가지는지 파악한다.
  • 데이터를 불러와서 EDA를 진행한다.

EDA 과정 중

  • 결측치를 isnull()이나 info()로 파악한다고 끝이 아니다. 지난번 당뇨병 데이터셋에서 봤듯이 결측치가 0으로 들어가 있을 수도 있다.
  • 이런 이유 뿐 아니라, 당연히 데이터를 전반적으로 파악하고 의미있거나 특이한 점을 찾기 위해 describe()를 살펴본다.
  • 전체 수치형 변수의 histogram 그려보기 도 꼭 진행하자! 맨날 까먹지 말고!
  • 이번 실습에서는 각 피쳐들의 scatterplot을 그려 변수들 사이의 대략적인 관계도 파악했었다.

전처리 과정 중

  • train set과 test set에 같은 전처리를 해줘야 함을 잊지 말자.
  • train에 한 전처리는 test에도!
  • encoding 등을 진행할때, test set을 활용하면 data leakage라고 하여 부정행위 처리되는 경진대회가 많다.
  • 꼭 그렇지 않더라도, train set을 기준으로 전처리 하는 습관을 들이자!
  • train과 test의 더미변수가 달라질 것 같다면 '기타'처리 해주는 스킬!

이상치 및 결측치 처리

  • 이상치인지, 입력 및 수집 과정 중 발생한 Error data인지 잘 판단해야한다.
  • 체감온도가 12.2로 전부 측정된 날이 하루 있었다.
    그래프를 통해 알 수 있었다.

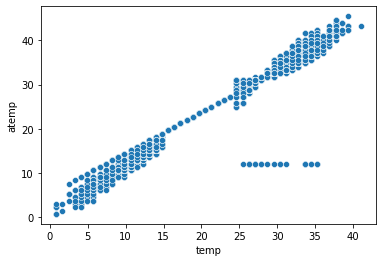
그래프를 잘 그려보고 잘 파악하자. 이런 경우 오류 데이터라고 파악할 수 있겠다.

  • 결측치... 제거를 할 수도, 대체를 할수도 있겠다. 일단 이번 실습에서는 0으로 되어있는 결측치들을 그대로 놔두었다.
  • 이상치... 도 마찬가지! ㅎ...
  • 결측치와 이상치의 처리가 가장 많이 생각해야하는 부분 아닐까..? 좀 더 고민을 해보자.

의문

풍속에 따른 대여 수

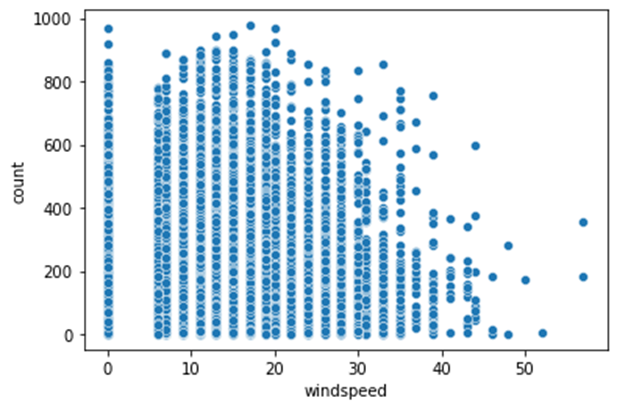
windspeed에 따른 대여 횟수의 scatterplot이다. 당연히 바람이 세게 불면 자전거를 빌리는 사람이 적을 것이라고 생각했고, 그래프를 보면, 바람이 세질수록, 대여 횟수의 최댓값이 작아지는 것은 확연하게 확인할 수 있다.

그러나, 점 하나하나가 데이터임을 명심하고 살펴보면, 풍속이 느리지만 자전거의 대여 횟수가 적은 데이터도 매우 많이 존재한다. 상관관계가 우리가 생각하던 대로 나오지 않은 것.
따라서 regplot을 그려보면 다음과 같은 형태다.

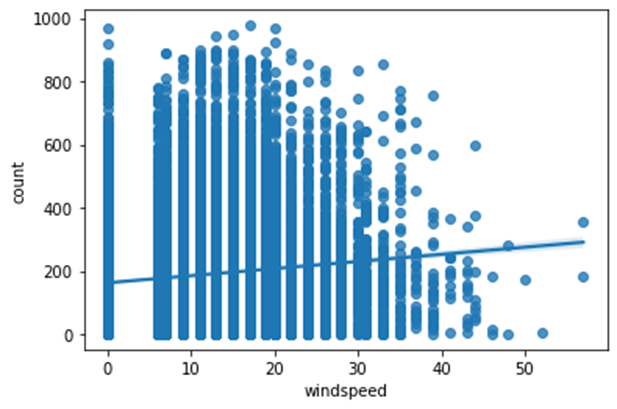
혹시 0으로 표시되어있는 결측치 때문인가 하여 결측치를 제거하고도 그려보았다.

wind_test = train.copy()
wind_test = wind_test.drop(wind_test[wind_test['windspeed'] == 0].index)
sns.regplot(data = wind_test, x='windspeed', y='count')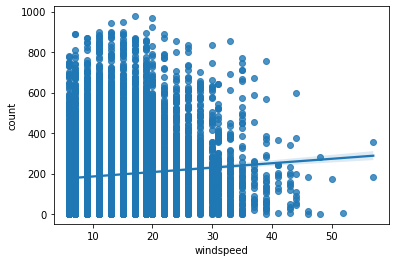

그래도 같다. 우리가 생각하던 경향과는 완전히 다른 추세선을 보이고 있다. 맨 위의 값들만 있으면 모르겠는데, 그 밑의 값들이 많이 존재하여 회귀선이 우리 생각과 다르게 나온다.
지금 우리가 사용하고 있는 RandomForestRegressor가 선형회귀 모델을 제작한다면, 저 regplot의 라인의 기울기가 windspeed에 대한 기울기(계수)가 되는 것 아닌가? 그렇다면 오히려 windspeed는 피쳐에서 제외하는게 맞는 것 아닌가? 아 너무 헷갈린다. 모르겠다.

그래서 feature에서 windspeed만 빼고 돌려봤다. 그리고 제출까지 해보았다.
0.002점 좋아진다.. 흠...

! 근데 지금 생각해보면, 결국 그래프가 저렇게 나왔다는 건, 바람이 세게 불면 사람들이 적게 빌리는 것은 맞지만, 바람이 적게 분다고 많이 빌리지도 않는다는 것!
바람이 세게 불면 대여가 줄어들기야 하겠지만, 그렇다고 해서 바람의 세기와 대여횟수 사이엔 상관관계가 없다는 것! 실제로 windspeed와 count 사이의 pearson 상관계수를 구해보면, 0.101369라는 작은 값이 나온다.
내가 생각했던 가설과 다르다고 해서 그냥 의미 없는 고민을 한 거구나! 데이터를 그대로 보지 않고 그냥 내 생각과 다르다고 이게 잘못되었다고 생각한건가? 그래프를 보던 상관계수를 보던 바람세기와 대여횟수의 관계는 바람이 셀수록 대여가 주는 것이 아니다! 내 상식과 내 마음대로 데이터를 곡해해서 해석하지 말아야겠다.

결론은 저걸 받아들이고, feature로 사용할지 안할지를 잘 선택하면 되겠다!
그럼 차라리 지난번에 한번 했던 것 처럼, 풍속이 몇 이상인지 아닌지를 0과 1로 구분해주는 컬럼을 만드는 건?

날씨에 따른 대여 수

날씨에 따른 대여 수를 살펴보았다.

sns.barplot(data= train, x='weather', y='count',ci=None)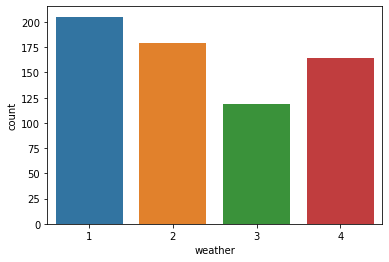

1~4로 갈수록 날씨가 좋지 않은 것인데, 날씨가 폭우 또는 폭설을 의미하는 4일때가 3일때보다 평균 대여수가 많다.
그래서 날씨가 4인 날을 살펴봤더니, 딱 하루, 그것도 딱 한시간이다.
따라서 평균 대여수가 날씨가 3인 날보다 더 많은 것이라고 예측해볼 수 있다.

그러면 여기서 남는 의문은, 과연 이 날씨가 4일때의 데이터를, 학습에 사용하는것이 맞는가..? 라는 의문이 남는다. 잘못된 일반화와 학습이 진행되는 건 아닐까..!

결론은 나지 않았지만, 지금 생각하기엔 ordinal encoding으로 되어있기에, 1~3까지의 경향이 충분히 반영된다면 4일때의 데이터를 빼고 학습시켜도 되지 않을까? 잘은 모르겠다..

특이했던 점

월에 따른 대여 수

월별 대여수의 그래프를 살펴보았다.

sns.barplot(data = train, x='month', y='count')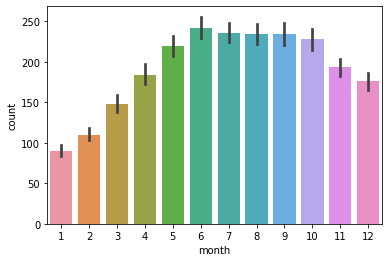

나름 의미있는 데이터인것 같아 보인다.

그러나, 년도에 따라 색상이 나누어지게 하여 살펴보았다.

sns.barplot(data = train, x='month', y='count', hue ='year')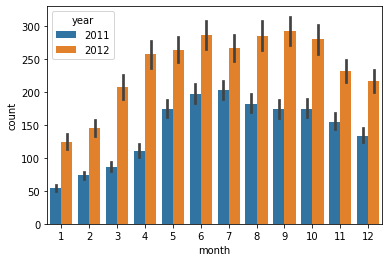

년도에 따라서 월별 대여수가 너무 차이가 많이 난다. 2012년이 2011년에 비해 확연히 많다. 심지어는 2011년의 12월 데이터와 2012년의 1월 데이터가 유사하다.

즉, 같은 달인데에도 연도에 따라 값이 차이가 많이 나기 때문에 오히려 성능을 저하시킬 수 있다. 따라서 피쳐에서 제외해주는 것이 좋다.

월별 경향은 분명히 존재하는 것 같으니, 이를 사용하고 싶다면 연-월 이라는 피쳐를 만들어 사용하는 방법도 있겠다. 약간 태블로에서의 불연속형 월과 연속형 월의 차이같은 느낌!

Day

Day를 살펴보면, train 데이터에는 1일부터 19일까지, test 데이터에는 20일부터 의 데이터만 존재한다. 따라서 day를 피쳐로 사용해 학습을 해봤자 그다지 도움이 되지 않는다는 것을 알 수 있고, 피쳐에서 제외해준다.
그리고 이는 train 과 test set을 day를 기준으로 나누었음을 짐작할 수 있게 해준다!

나는 사실 day는 뭐 크게 영향이 없을 것 같아 피쳐에서 제외했고, month는 season과 어느정도 겹치는 부분 아닌가 해서 제외했는데.. 우연히 제거해야하는 것들을 제거한 셈..!

회귀 평가 지표

오늘의 가장 어려웠던 것..!

MAE

abs(y_train - y_valid_pred).mean()

from sklearn.metrics import mean_absolute_error
mean_absolute_error(y_train, y_valid_pred)
  • 실제값 - 예측값의 절댓값의 평균
  • 절대값을 취하기 때문에 가장 직관적임
  • 단위 자체가 기존 데이터와 동일하여 오차를 쉽게 파악할 수 있다.

MSE

((y_train - y_valid_pred) ** 2).mean()

from sklearn.metrics import mean_squared_error
mean_squared_error(y_train, y_valid_pred)
  • 실제값 - 예측값의 제곱의 평균
  • 제곱을 하기 때문에 특이치에 민감하다. (실제값과 예측값의 차이가 클수록 훨씬 증가한다.)

RMSE

np.sqrt(((y_train - y_valid_pred) ** 2).mean())
  • 실제값 - 예측값의 제곱의 평균에 루트를 씌운 값
  • 실제 값과 유사한 단위로 다시 변환(다시 루트를 씌우므로)하여 MSE보다 해석이 더 쉽다.
  • MAE보다 특이치에 Robust(강건)

RMSLE

((np.log1p(y_train) - np.log1p(y_valid_pred)) ** 2).mean() ** 0.5
# log1p는 1을 더한 후 로그를 취해주는 함수

# 또는
from sklearn.metrics import mean_squared_log_error
rmsle = np.sqrt(mean_squared_log_error(y_train, y_valid_pred))
rmsle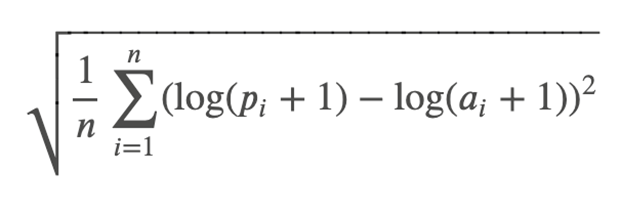

  • RSME와 유사하나, 실제값과 예측값 대신 해당 값들에 1을 더하고 로그를 취한 값을 사용.

  • 1을 더해주는 이유?

로그 함수의 그래프. x 가 1보다 작으면 로그 값이 음수가 나온다. 따라서 1을 더해서 로그를 씌운 결과가 음의 무한대로 발산하는 것을 방지!

  • 로그를 취해주는 이유는?
    로그를 취해주면,
    scaling 되는 효과가 있다. 값의 범위가 줄어든다.
    분포가 정규분포에 가까운 형태가 된다.
    한쪽으로 skewed 되있던 것이 좀 풀린다.

라고 하는데, 솔직히 바로 납득은 안간다. 좀 더 써보고 공부해봐야 왜 로그를 씌워서 사용하는지 알 것 같다.

  • RMSLE의 특징
  1. 이상치에 강건하다.
    log를 씌워 값의 scale을 줄여주었기 때문에 이상치에 비교적 강건하다.
  2. 상대적 오차를 측정해준다.
    식을 생각해보면 log(실제값 + 1) - log(예측값 + 1)인데, 이는 log((실제값 + 1) / (예측값 + 1))이다. 따라서 RMSLE는 값이 변화한 비율을 나타내는 상대적 오차라고 볼 수 있다.
  3. Underestimating에 대하여 더 가중치를 둔다.
    음 log함수를 생각해보면, X값이 작아질수록 미분계수가 증가한다. 따라서 예측값이 실제값보다 작은 경우가, 큰 경우에 비해 log값의 차이가 크므로 RMSLE값이 크다.
  4. 작은 값들에 대해 크다.
    3번에서의 내용을 일반화시키면 이렇게 볼 수 있지 않을까?
    값이 작을수록 log 함수의 미분계수는 크다. 두 값의 차가 일정하다면, 두 값이 7,10일때보다 4,7일때 log 값의 차 역시 크다. 따라서 RMSLE는 작은 값들에 대해 더 크게 나타나는 효과를 가진다.

4번은 사실 수업들으면서 헷갈렸던 부분이라 확실하지는 않다. 큰 값과 작은 값의 기준도 모호하긴 하고, 그래도 일단은 이런 식으로 알고 있으면 될 것 같다.

  • 오차의 가중치

RMSLE는 log 기반이므로 수치가 작은 값들에 대해 더 크게 나타나는 효과를 가진다.
약간 결은 다르지만,
위에서 MSE는 잔차의 제곱으로 나타내므로, 실제값과 예측값의 차가 큰 값에 대해 더 크게 나타나는 효과를 가졌었다. RMSE도 당연히 마찬가지고!
MAE는 절댓값을 이용하므로 값의 크기에 따른 가중치가 없다!

RMSLE는 다른 오차들과는 다르게 상대적 오차((실제값 + 1) / (예측값 + 1)) 를 나타내기 때문에, 잔차(실제값 - 예측값)의 크기에 따른 가중치는 특정할 수 없겠다. 그것보다는 값들 자체의 절대적인 수치가 작을때 RMSLE가 커진다고 받아들였다.

  • 근데 이해가 안된 것
    RMSLE 는 최솟값과 최댓값의 차이가 큰 값에 주로 사용됩니다. 라고 강사님이 말씀해주셨다. 으악 이건 또 왜지.. 좀 더 생각을 해봐야겠다.... 아마 상대적 오차를 나타내어주기 때문 아닐까! 다른 MSE 등을 이용하면 값이 너무 커질테니까!

오늘의 결론 :

진짜 EDA가 중요하구나...!

EDA를 정말 꼼꼼히 잘 해보는게 머신러닝에 있어서 아주 중요함을 느낀 하루.

기타

  • 미니프로젝트 진행할때, feature_importances도 안봤다... 이으이 정신 차리자! 잘 기억해보자!
  • 경진대회의 점수를 올리기 위해 가장 중요한 것은 EDA이다! feature engineering은 오히려 할수록 점수가 떨어지는 경우도 많고 그렇다. 따라서 다양한 분야의 사람들, 도메인 전문가, 프로그래머, 데이터 사이언티스트 등이 모여 팀을 꾸린다.

더 공부해볼 것

  • 이론과 정리만 말고.. 진짜 실습의 필요성을 느끼고 있다!
  • 이상치와 결측치의 판단 및 처리 기준을 끊임없이 고민해야할 듯.
  • 어떤 평가기준을 언제 사용할지에 대한 고민 역시 필요!
  • 회귀의 평가 지표는 더더 공부가 필요하다.
  • 피쳐를 선택해주는 기준에 대한 고민 (feature importance 보기? 상관계수?)
  • 다중공선성? 에 대한 내용을 좀 찾아보자. month와 season?
  • 다들 Xgboost, lightGBM같은 모델들을 공부해서 미니프로젝트에 사용했더라...!
  • 나도 배운것에만 의존해서 하려하지 말고, 스스로 더 찾아내고 공부하여 활용하고자 하는 마음가짐...! 을 가지자.
  • 이 실습에서 더 해봐야 할것? 결측치 및 이상치 처리.. feauture engineering!

참고자료.

요즘 항상 너무 늦게 시작해서, 시간이 없다는 핑계로 자세히 공부 안하고 넘어가는데...
반성하자!
회귀의 평가지표에 대한 자세한 내용을 더 공부해보고 싶다. 자료가 별로 없나..? 통계학 쪽인가..?
결측치와 이상치 처리를 어떻게 해봐야 할 지도 생각해봐야겠고
어떤 피쳐를 사용하는게 옳은지에 대한 판단도 더 연습해봐야 한다!

그리고 아까도 생각했지만, 정리 하나하나에 매몰되지 말고, 오늘 수업 전체의 흐름을 생각하자!
다시 전체 한번 훑어보고 머릿속으로 정리하고 자자.

학교 원드라이브 계정이 변경된다고 그러더니, 동기화 오류가 났다. 필기 날라가진 않겠지?..

profile
임종우
ai school 기간 동안의 TIL!
이전 포스트

[Day 38] Tableau 기초 (2)

다음 포스트

[Day 40, 41] feature engineering

0개의 댓글