👨‍🏫 본 글은 칸 아카데미의 수업을 듣고 정리한 글 입니다.

• Linear transformation examples: Scaling and reflections
• Linear transformation examples: Rotations R2
• Rotation in R3 around the x-axis
• Unit Vector
• Introduction to projections
• Expressing a projections on to a line as a matrix vector prod

---

Linear transformation examples: Scaling and reflections

🎈 오늘은 선형변환의 예시들 중 reflections과 Scaling에 관해 학습합니다. 오늘 강의 같은 경우에는 이해하는데 어렵지 않으며, 당연한 이야기를 하는 것이라고도 할 수 있지만, 중요한 부분이라고 생각됩니다.

🎈 선형변환은 단위행렬을 사용해 위와 같이 표현할 수 있습니다. 이는 선형변환을 이해하는데 매우 중요한 요소이며, 이를 통해 쉽게 이해할 수 있습니다.

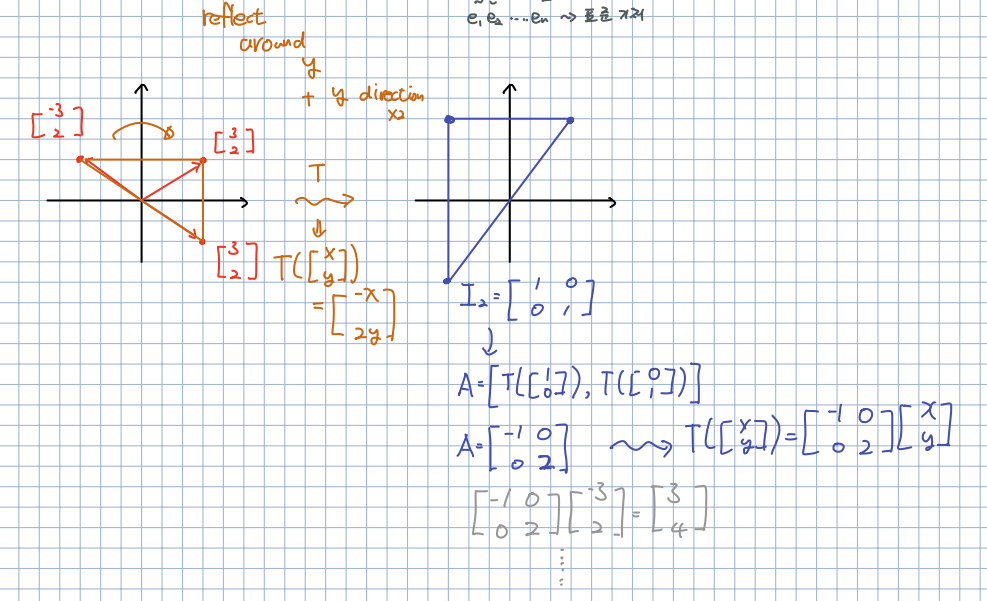
🎈 먼저 3개의 점을 가르키는 포지션 벡터들을 사용해 삼각형을 만듭니다. 이 삼각형을 이루는 벡터들을 y축으로 reflect하고 길이를 2배 변환할려고 합니다. 식으로 표현하면 $T([x,y]^T)$= $[-x, 2y]^T$라고 표현할 수 있습니다. 이는 단위행렬을 사용하면 더욱 간단하면서 직관적으로 이해할 수 있습니다. 단위행렬의 표준기저들을 사용해 다시 표현할 수 있으며, 이를 사용해 쉽게 선형변환을 진행할 수 있습니다.

Linear transformation examples: Rotations R2

🎈 이어서 $\theta$만큼 회전하는 선형변환에 대해 학습합니다. $ROT_{\theta}(\vec{x})$라고 하면 $\vec{x}$ 반시계 방향으로 $\theta$만큼 회전하는 변환이라고 말할 수 있습니다.

🎈 먼저 $ROT_{\theta}(\vec{x})$을 선형변환이라고 말하기 위해선 가산성과 동차성을 확인해야합니다. 이는 간단하게 그래프를 통해 확인할 수 있습니다.

🎈 역시나 단위행렬을 사용해 위와 같이 삼각함수로 rotation을 수행할 수 있습니다. 이는 좌표만 알고있다면 언제든지 원하는 각도만큼 회전할 수 있습니다.

Rotation in R3 around the x-axis

🎈 이번 강의에서는 3차원에서의 Rotation에 대해 학습합니다.

🎈 3차원에서 3차원으로 x축을 중심으로 $\theta$만큼 transformation을 하는 변환이라고 가정합니다.

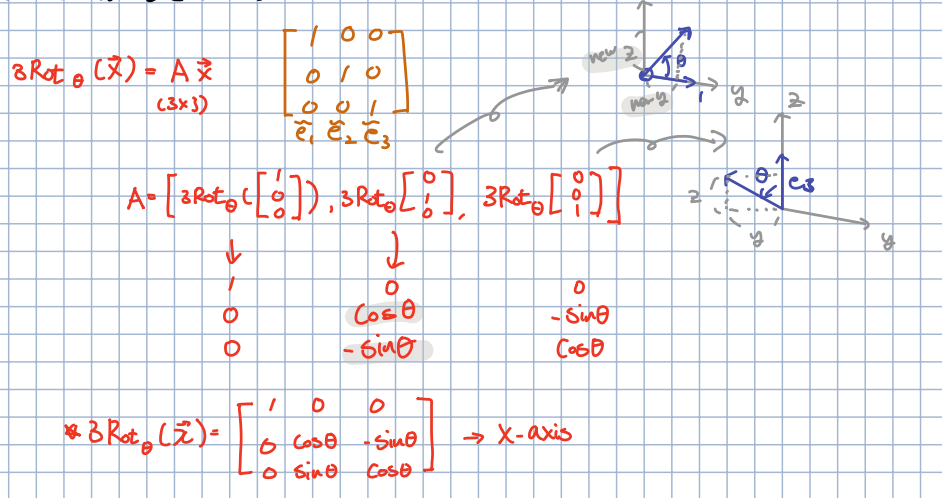
🎈 앞서 배운 것과 동일하게 단위벡터를 사용해 계산할 수 있습니다. 먼저 x축을 의미하는 e1은 그대로 일 것이며, 나머지 e2, e3의 경우 그래프를 통해 각각 삼각함수로 표현할 수 있습니다.

Unit vectors

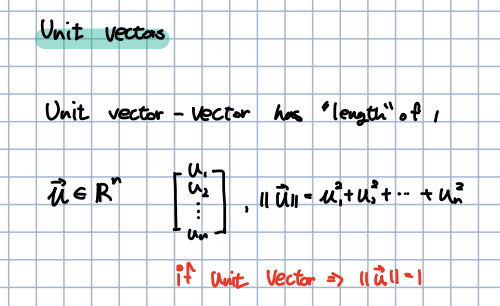
🎈 어떤 벡터의 길이가 1인 벡터를 Unit vector라고 부릅니다.

🎈 그렇다면 같은 방향을 가리키는 벡터의 Unit vector는 어떻게 찾을 수 있을까요? 위의 공식으로 어렵지 않게 Unit vector를 찾을 수 있으며, 이는 normalize 한다 라고도 표현합니다.

Introduction to projections

🎈 이번 강의에서는 정사영에 대해 학습합니다.

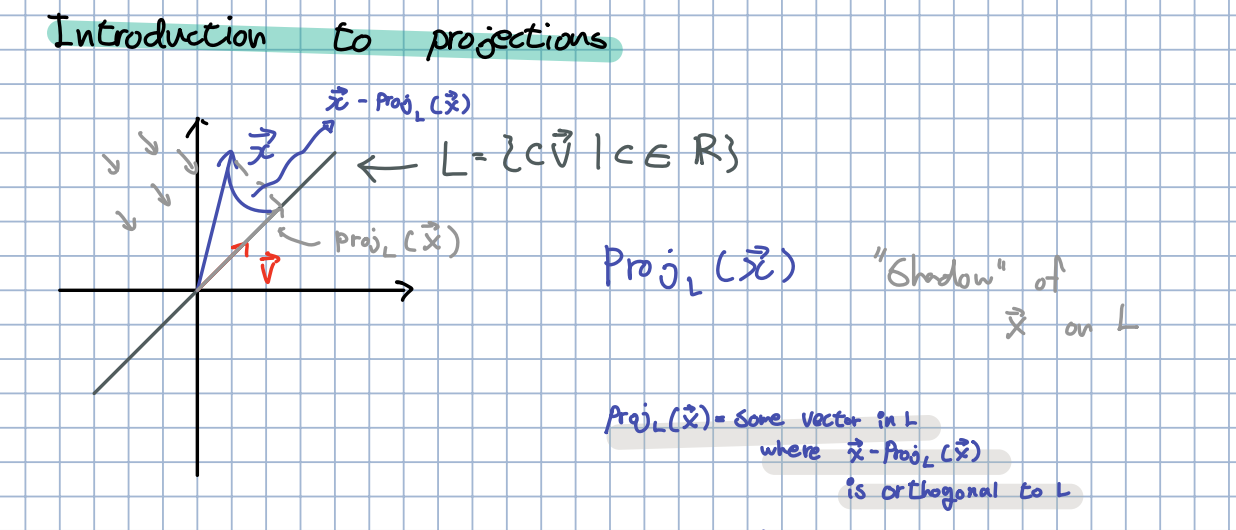
🎈 $c\vec{v}$로 이루어진 집합 $L$을 가정하고, 임의의 $\vec{x}$ 벡터의 정사영을 투영합니다. 이를 위의 그래프로 표현할 수 있으며, $Proj_L(\vec{x})$는 Some Vector in L where $\vec{x}$-$Proj_L(\vec{x})$ is orthogonal to L 라고 말할 수 있습니다.

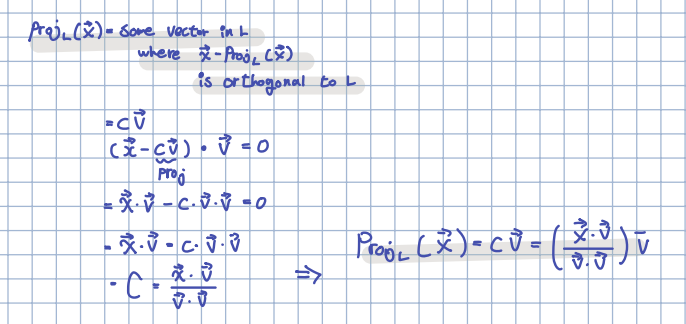
🎈 위의 특징을 사용해 스칼라 $C$를 찾을 수 있습니다. 스칼라 $C$를 사용해 정사영의 벡터를 찾을 수 있습니다.

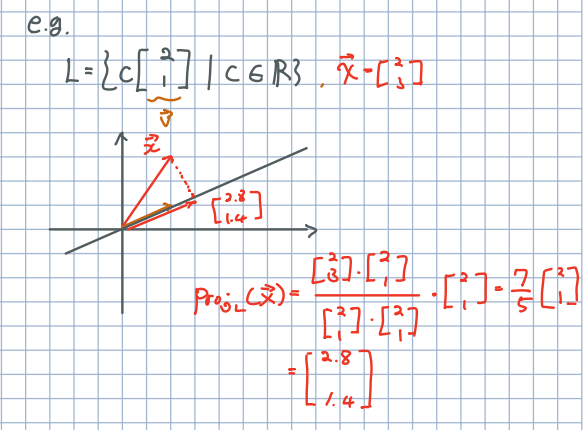
🎈 위의 예시를 통해 직관적으로 정사영을 확인할 수 있습니다.

Expressing a projection on to a line as matrix vector prod

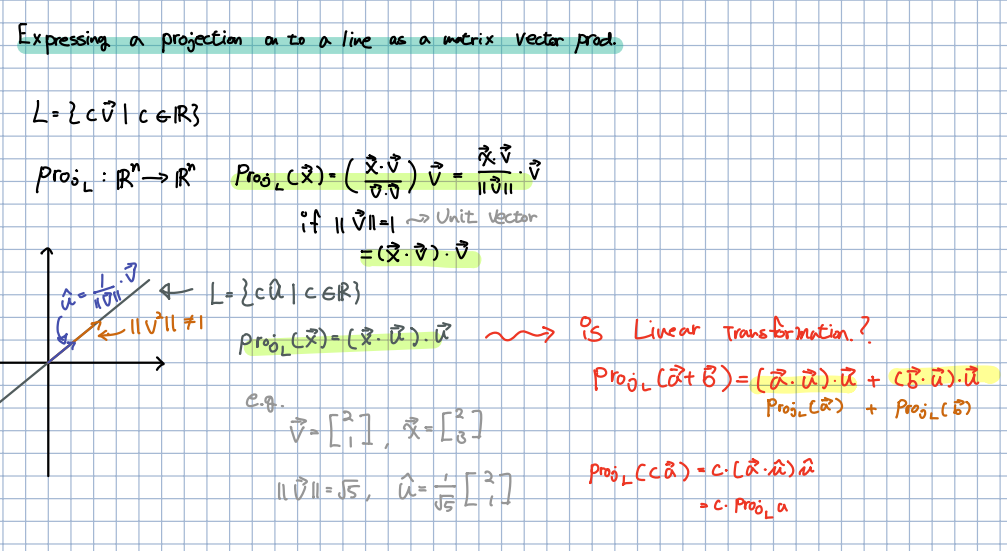
🎈 위에서 배운 정사영을 선형변환으로 표현하는 것에 대해 학습합니다. 위에서 학습한 정사영 식에 분모부분을 $\vec{v}$의 길이라고 표현할 수 있으며, 길이가 만약 1이면 $\vec{v}$가 Unit vector라고 말할 수 있으며, 이 Unit vector를 사용해 정사영 식을 정의할 수 있습니다.

🎈 그렇다면 이 정사영 식이 선형변환한다고 말할 수 있을까요? 이는 선형 변환의 두 가지 조건을 확인해보면 알 수 있습니다. 가산성과 동차성을 확인해보면 이는 선형변환 하다는 것을 알 수 있습니다.

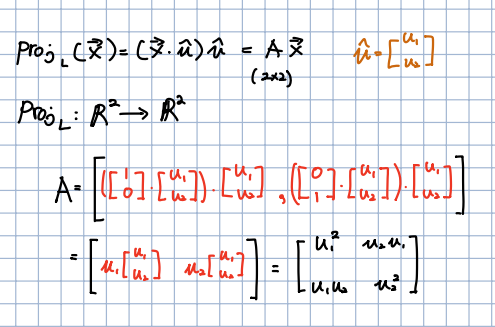
🎈 선형 변환임을 알았기 때문에, 다시 $A\vec{x}$로 표현할 수 있습니다. 이를 2x2 단위 행렬의 표준 기저 벡터들을 사용해 행렬 A를 찾을 수 있습니다. 결과적으로 임의의 $\vec{x}$를 알고 있다면, 행렬 A를 사용해 정사영을 계산할 수 있습니다.